
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные формулы комбинаторикиСтр 1 из 8Следующая ⇒
Лекция 1. Теория вероятностей. Основные понятия. Событием называется всякий факт, который может произойти или не произойти в результате опыта. При этом тот или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда. События называются несовместными, если появление одного из них исключает появление других. Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте). Полной группой событий называется совокупность всех возможных результатов опыта. Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта. Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью. В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров. Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного. Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А. Вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей
Пример 1. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым. Решение. Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С. Тогда в соответствием с записанными выше формулами получаем:
Отметим, что вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий.
Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов. Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта. Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна: Как видно, эта величина не совпадает с найденной вероятностью.
При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события. Классическое определение вероятности неприменимо к испытаниям с бесконечным числом исходов. Чтобы преодолеть этот недостаток вводится понятие геометрической вероятности, т.е. вероятности попадания точки в какой – либо отрезок или часть плоскости (пространства). Так если на отрезке длиной L выделен отрезок длины l, то вероятность попадания наугад взятой точки в отрезок l равна отношению l/L.
Пример 2. Из полной колоды игральных карт извлекается наудачу одна карта. Найти вероятность того, что эта карта окажется: 1) тузом; 2) пиковой масти; 3) пиковым тузом. Решение. 1) Так как число карт полной колоды равно 2) Общее число карт пиковой масти равно 13. Поэтому вероятность извлечения карты этой масти равна
3) Вероятность извлечения туза пик равна
Пример 3. В партии из Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди Искомая вероятность:
Лекция 2. Операции над событиями Теорема сложения вероятностей несовместных событий Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Для большого числа несовместных событий:
Если события
Пример 1. Зависимы или независимы: 1) несовместные события; 2) события, образующие полную группу; 3) равновозможные события? Решение. 1) Зависимы, так как появление любого из них обращает в нуль вероятности всех остальных; 2) зависимы, так как непоявление всех, кроме одного, обращает в единицу вероятность последнего; 3) могут быть как зависимы, так и независимы.
Пример 2. Из полной колоды карт (52 листа) вынимается одна карта. Рассматриваются события:
Зависимы или независимы следующие пары событий: 1) Решение. 1) независимы, так как 2) зависимы, так как 3) зависимы, так как 4) независимы, так как 5) зависимы, так как несовместны.
Пример 3. На стеллаже в библиотеке в случайном порядке расставлены 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие Решение. Первый способ. Событие
По теореме сложения
Окончательно получим
Второй способ. События
Вероятность
Пример 4. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта. Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В. Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого. Всего в колоде 13 червонных и 13 бубновых карт.
При вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна Тогда
Пример 5. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей? Вероятность выпадения 6 очков при одном броске кости равна
Пример 6. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие
Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна
Вероятность того, что второй стрелок попадет в цель, а первый – нет равна
Тогда вероятность попадания в цель только одним стрелком равна
Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:
Тогда вероятность того, что в цель попадет только один стрелок равна:
Пример 7. Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится: а) не более, чем в трех ящиках; б) не менее, чем в двух ящиках.
а) Вероятность того, что данная деталь находится во всех четырех ящиках, равна
Вероятность того, что нужная деталь находиться не более, чем в трех ящиках равна вероятности того, что она не находится во всех четырех ящиках.
б) Вероятность того, что нужная деталь находится не менее, чем в двух ящиках, складывается из вероятностей того, что деталь находиться только в двух ящиках, только в трех ящиках, только в четырех ящиках. Конечно, эти вероятности можно посчитать, а потом сложить, однако, проще поступить иначе. Та же вероятность равна вероятности того, что деталь не находится только в одном ящике и имеется вообще.
Лекция 3. Формула Бейеса. Пусть имеется полная группа несовместных гипотез Требуется определить какие вероятности имеют гипотезы Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
Эта формула называется формулой Бейеса.
Пример 2. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй — 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом. Решение. Обозначим через Условная вероятность того, что деталь будет отличного качества, если она произведена первым автоматом, равна Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна
Искомая вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Байеса равна
Лекция 4. Решение. По условию задачи
Пример 2. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз. Решение. Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий. Т.к. выстрелы независимы, то можно применить формулу Бернулли вероятности того, что в т испытаниях событие в вероятностью р наступает ровно п раз.
В случае пяти попаданий из пяти возможных: Четыре попадания из пяти выстрелов: Три попадания из пяти: Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:
Пример 3. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг. Решение. По условию,
Найдем
Искомая вероятность
Лекция 5. Биноминальное распределение Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p. Примем число появлений события в каждом из испытаний за некоторую случайную величину Х. Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности. Значения найти достаточно просто. Очевидно, что в результате п испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. до п раз. Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.
Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.
Распределение Пуассона. Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Если число испытаний п достаточно велико, а вероятность появления события А в каждом испытании мало (p £0,1), то для нахождения вероятности появления события А k раз находится по формуле распределения Пуассона:
Если известны числа l и k, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона. Числовые характеристики дискретных случайных величин Закон распределения полностью характеризует случайную величину. Однако, когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.
Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно. С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Вычисление дисперсии. Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания.
Доказательство. С учетом того, что математическое ожидание М(Х) и квадрат математического ожидания М2(Х) – величины постоянные, можно записать:
Применим эту формулу для рассмотренного выше примера:
Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Справедливость этого равенства вытекает из свойства 2.
Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в каждом испытании.
Лекция 6. Функция распределения. Во всех рассмотренных в лекции 5 случаях, случайная величина определялась путем задания значений самой величины и вероятностей этих значений. Однако, такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально. Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов? Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин. Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. Х < x, обозначим через F(x). Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.
Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения. Для дискретной случайной величины функция распределения имеет вид:
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х. Плотность распределения.
Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема. Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов. После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением(может быть, конечного числа точек. Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b. Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
Равномерное распределение. Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [ a, b ], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю.
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения.
f(x)
0 a b x Получаем Найдем функцию распределения F(x) на отрезке [ a,b ].
F(x)
0 a b x
Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны. Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.
Вероятность попадания случайной величины в заданный интервал:
Функция Лапласа.
Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.
Обозначим Тогда Т.к. интеграл
которая называется функцией Лапласа или интегралом вероятностей. Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах. Ниже показан график функции Лапласа.
Функция Лапласа обладает следующими свойствами: 1) Ф(0) = 0; 2) Ф(- х) = - Ф(х); 3) Ф(¥) = 1. Функцию Лапласа также называют функцией ошибок и обозначают erf x.
Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:
Ниже показан график нормированной функции Лапласа.
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Это правило называется правилом трех сигм. Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожидание а = 65 т и средним квадратичным отклонением s = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется. Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т. Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально. Получаем:
ПО ЕЕ ВЫБОРКЕ Пусть в эксперименте изучается случайная величина X и, из теоретических соображений, известен ее закон распределения. Естественно, возникает задача оценки (приближенного нахождения) параметров Обычно в распоряжении исследователя имеются лишь данные выборки генеральной совокупности, например ( 1. Числовые характеристики выборки. Выборочной средней
Если же значения выборки
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения Выборочной дисперсией Если все значения
Если же значения признака
Можно показать, что
Выборочным средним квадратическим отклонением
Особенность
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.24.134 (0.323 с.) |
 .
.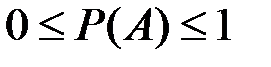 .
.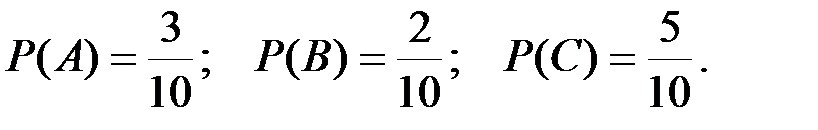
 .
. , и каждая из них имеет одинаковую вероятность быть извлеченной из колоды, а число тузов в колоде
, и каждая из них имеет одинаковую вероятность быть извлеченной из колоды, а число тузов в колоде  , поэтому вероятность извлечения туза равна
, поэтому вероятность извлечения туза равна 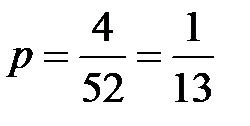 .
. .
. .
. деталей имеется
деталей имеется  стандартных. Наудачу отобраны
стандартных. Наудачу отобраны  деталей. Найти вероятность того, что среди отобранных деталей ровно
деталей. Найти вероятность того, что среди отобранных деталей ровно 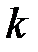 стандартных.
стандартных. – числу сочетаний из
– числу сочетаний из  способами; при этом остальные
способами; при этом остальные 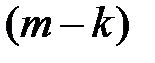 деталей должны быть нестандартными и взять их из
деталей должны быть нестандартными и взять их из  нестандартных деталей можно
нестандартных деталей можно  способами. Следовательно, число благоприятных исходов равно
способами. Следовательно, число благоприятных исходов равно  .
. .
. .
.
 несовместны и образуют полную группу, то сумма их вероятностей равна единице:
несовместны и образуют полную группу, то сумма их вероятностей равна единице: .
. – появление туза;
– появление туза; – появление карты красной масти;
– появление карты красной масти; – появление бубнового туза;
– появление бубнового туза; – появление десятки.
– появление десятки. ;
;  ;
; ;
;  ;
; ;
;  ;
; ;
; .
.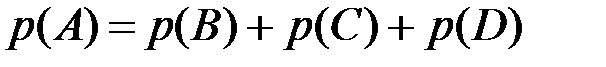 ,
, ,
,  ,
,  .
.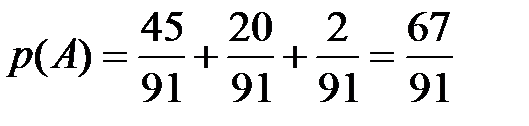 .
. (ни один из взятых трех учебников не имеет переплета) – противоположные, поэтому
(ни один из взятых трех учебников не имеет переплета) – противоположные, поэтому .
. .
. , при вытаскивании второй карты -
, при вытаскивании второй карты -  , третьей -
, третьей -  , четвертой -
, четвертой -  .
. .
. .
. . Вероятность того, что не выпадет 6 очков -
. Вероятность того, что не выпадет 6 очков -  . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна
. Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна  . Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна
. Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна  .
. , промах второго – событие
, промах второго – событие  .
.
 .
. .
. .
.


 .
. с известными вероятностями их наступления
с известными вероятностями их наступления  . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
. Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности  .
.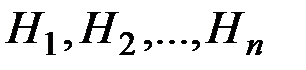 относительно события А, т.е. условные вероятности
относительно события А, т.е. условные вероятности  .
.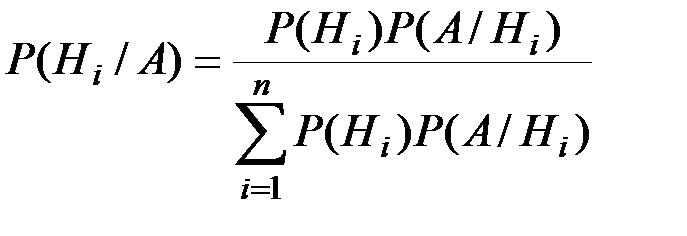 .
. событие-деталь отличногокачества. Можно сделать два предположения (гипотезы):
событие-деталь отличногокачества. Можно сделать два предположения (гипотезы):  - детальпроизведена первым автоматом, причем (поскольку первый автоматпроизводит вдвое больше деталей, чем второй, т.е. из трех произведенных деталей две произведены первым автоматом, а одна вторым)
- детальпроизведена первым автоматом, причем (поскольку первый автоматпроизводит вдвое больше деталей, чем второй, т.е. из трех произведенных деталей две произведены первым автоматом, а одна вторым) 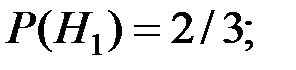
 - деталь произведена вторым автоматом, причем
- деталь произведена вторым автоматом, причем 
 Условная вероятность того, что деталь будет отличного качества, если она произведена вторым автоматом, равна
Условная вероятность того, что деталь будет отличного качества, если она произведена вторым автоматом, равна 
 .
.
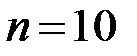 ,
, 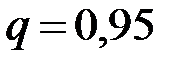 ,
,  . Тогда по формуле Бернулли получаем
. Тогда по формуле Бернулли получаем .
.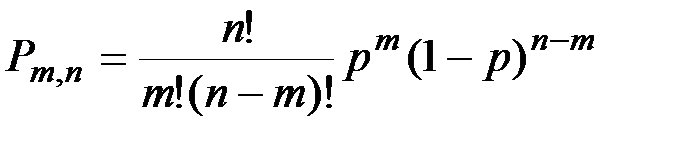 .
. .
. .
.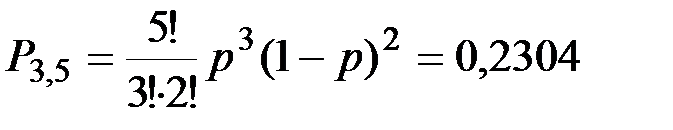 .
. .
. =100 000,
=100 000,  = 0,0001,
= 0,0001,  = 5. События, состоящие в том, что книги сброшюрованы неправильно, независимы, число n велико, а вероятность
= 5. События, состоящие в том, что книги сброшюрованы неправильно, независимы, число n велико, а вероятность  .
. :
: .
. .
.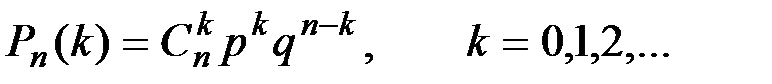
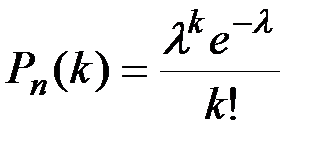 .
.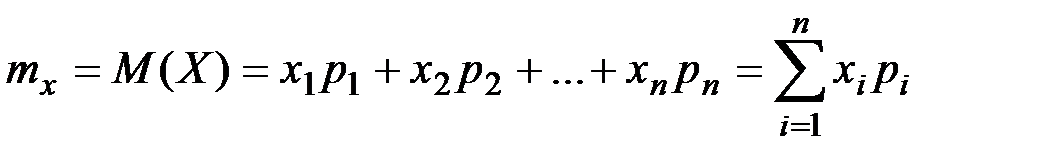 .
.





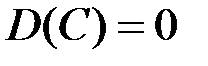 .
.






 .
.












 не выражается через элементарные функции, то вводится в рассмотрение функция
не выражается через элементарные функции, то вводится в рассмотрение функция ,
,



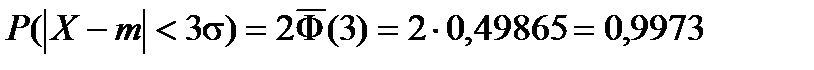

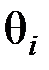 , которыми определяется это распределение. Например, если известно, что случайная величина
, которыми определяется это распределение. Например, если известно, что случайная величина  распределена в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание
распределена в генеральной совокупности нормально, то необходимо оценить, т. е. приближенно найти математическое ожидание  и среднее квадратическое отклонение
и среднее квадратическое отклонение  , так как эти два параметра полностью определяют нормальное распределение.
, так как эти два параметра полностью определяют нормальное распределение. ), полученные в результате п наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.
), полученные в результате п наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.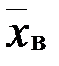 называется среднее арифметическое всех значений выборки. Если все значения
называется среднее арифметическое всех значений выборки. Если все значения  выборки объема п различны, то
выборки объема п различны, то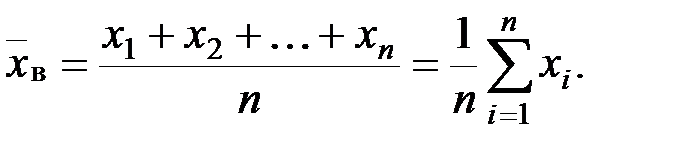
 имеют соответственно частоты
имеют соответственно частоты 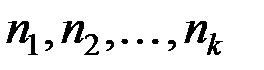 , причем
, причем  :
: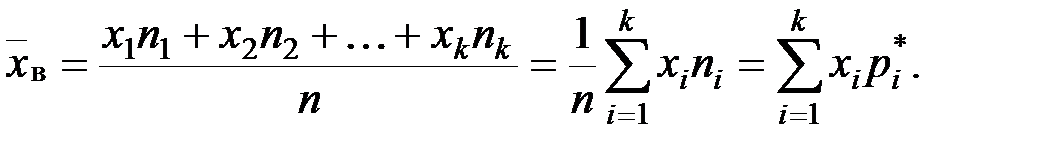
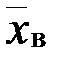 , вводят выборочную дисперсию.
, вводят выборочную дисперсию. называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней
называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней  .
.


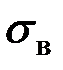 называется квадратный корень из выборочной дисперсии:
называется квадратный корень из выборочной дисперсии: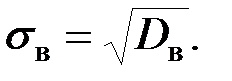
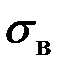 состоит в том, что оно измеряется в тех же единицах, что и измеряемый признак.
состоит в том, что оно измеряется в тех же единицах, что и измеряемый признак.


