
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерная непрерывность функций. ⇐ ПредыдущаяСтр 5 из 5
Определение. Функция f(x), определенная на промежутке Х, называется равномерно непрерывной на промежутке Х, если
Примеры. 1) f(x)=x, xÎ(-¥;+¥) Т.к. |f(х1)- f(x2)ê=êх1-х2ê, то
2) f(x)=sin х, xÎ(-¥;+¥) Выше показали, что |sin x1-sin x2|£|x1-x2| 3) f(x)=х2, xÎ[-1,1] |f(х1)- f(x2)ê=
4) f(x)=х2, xÎ(-¥;+¥) – не является равномерно непрерывной. Отрицание равномерной непрерывности:
Тогда, пусть
Возьмем х1= Теорема Кантора. Если функция f(x) определена и непрерывна на отрезке [a,b], то она и равномерно непрерывна на этом отрезке. Доказательство. Допустим противное, т.е. функция f(x) определена и непрерывна на отрезке [a,b], но неравномерно непрерывна на нем, т.е. Это означает, что найдется хотя бы одно e0>0, которому не отвечает никакое d>0 в смысле определения равномерной непрерывности В этом случае, какое бы число d>0 ни взять, найдутся в промежутке [a,b] такие два значения х¢ и х¢¢, что Возьмем последовательность положительных чисел такую, что {dn}→0, n→¥. Тогда Последовательность {x¢n} – ограничена (т.к. ее значения находятся внутри отрезка). По лемме Больцано-Вейерштрасса, из ограниченной последовательности можно извлечь сходящуюся подпоследовательность Т.к. Рассмотрим разность f( Получили противоречие с условием Непрерывность и разрывы монотонной функции. Пусть функция f(x) определена и монотонна на промежутке Х. Теорема 1. Монотонная функция может иметь в Х точки разрыва только 1-го рода. Доказательство. Пусть функция f(x) возрастает и с – точка разрыва (c – не является левым концом промежутка Х). Слева от с функция f(x) возрастает, следовательно f(x)£f(с) Т.о. монотонная функция f(x) является ограниченной (числом f(с)) По теореме о пределе монотонной функции, f(x) имеет конечный предел слева:
f(с-0)= Если f(с-0)=f(с), то слева в точке с функция f(x) непрерывна. В противном случае – с – точка разрыва 1-го рода. Аналогично доказывается, что в каждой точке с промежутка Х, не являющейся его правым концом, справа тоже либо имеет место непрерывность, либо разрыв 1-го рода. Существование и непрерывность обратной функции. Определение. Пусть функция f:A→B. 1) Если 2) Если f(A)=B или Отображение f которое одновременно является инъекцией и сюръекцией, называется биекцией или взаимно однозначным соответствием между А и В. Можно определить новую функцию: f-1:B→A, x=f-1(y)–обратная функция, относительно f. Теорема (б.д.). Пустьфункция у=f(x) определена и непрерывна на отрезке [a,b] и является на нем строго возрастающей. Тогда у функции у=f(x) есть обратная функция х=g(y), определенная на отрезке [p,q], где p=f(a), q=f(b), причем эта функция строго возрастающая и непрерывная в промежутке [p,q]. Замечание 1. Аналогичная теорема имеет место для строго убывающих функций: Пустьфункция у=f(x) определена и непрерывна на отрезке [a,b] и является на нем строго убывающей. Тогда у функции у=f(x) есть обратная функция х=g(y), определенная на отрезке [p,q], где p=f(b), q=f(а), причем эта функция строго убывающая и непрерывная в промежутке [p,q]. Замечание 2. Справедливы также следующие утверждения. Утверждение 1. Пустьфункция у=f(x) определена и непрерывна в промежутке (a,b) и является на нем строго возрастающей. Тогда у функции у=f(x) есть обратная функция х=g(y), определенная в промежутке (p,q), где p= Утверждение 2. Пустьфункция у=f(x) определена и непрерывна в промежутке (a,b) и является на нем строго убывающей. Тогда у функции у=f(x) есть обратная функция х=g(y), определенная в промежутке (p,q), где p= Замечание 3. Некоторые из чисел a,b,p,q могут быть несобственными.
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.105.124 (0.01 с.) |
 e>0
e>0 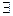 δ=δ(e)
δ=δ(e)  |f(х1)-f(x2)|<e
|f(х1)-f(x2)|<e êх1-х2êêх1+х2ê£2êх1-х2ê
êх1-х2êêх1+х2ê£2êх1-х2ê
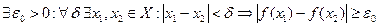
 ,
, 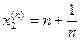 ,
,  -
-  →0, n→¥
→0, n→¥ 5) f(x)=
5) f(x)=  не является равномерно непрерывной на промежутке (0,1].
не является равномерно непрерывной на промежутке (0,1]. , х2=
, х2=  . Тогда
. Тогда 

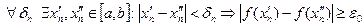
 , k®¥,
, k®¥,  Î[a,b].
Î[a,b]. (т.к.
(т.к.  , а dn→0, n→¥), то и последовательность
, а dn→0, n→¥), то и последовательность  , k®¥.
, k®¥. )-f(
)-f( ). Т.к. функция f(x) непрерывна на отрезке [a,b], то она непрерывна и в точке
). Т.к. функция f(x) непрерывна на отрезке [a,b], то она непрерывна и в точке  , следовательно, допущение неверно и функция равномерно непрерывна. Ч.т.д.
, следовательно, допущение неверно и функция равномерно непрерывна. Ч.т.д. £f(с)
£f(с)
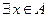 такое, что y=f(x), то отображение f действует на В (отображение «на»). Такое отображение также называется сюръекцией.
такое, что y=f(x), то отображение f действует на В (отображение «на»). Такое отображение также называется сюръекцией. , q=
, q=  , причем эта функция строго возрастающая и непрерывная в промежутке (p,q)
, причем эта функция строго возрастающая и непрерывная в промежутке (p,q)


