Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признаки сходимости числовых положительных рядов.Стр 1 из 4Следующая ⇒
Признаки сходимости числовых положительных рядов. Необходимый признак. Определения . Пусть задана бесконечная последовательность чисел: u1, u2, …, un, … Построим из этой последовательности выражение: u1+ u2 + u3 +…+ un +… Это выражение называется числовым рядом, где слагаемые u1, u2, u3,… называются членами ряда, а член un - его общим членом. Таким образом, можно сказать, что числовой ряд – это бесконечная сумма чисел Числовой ряд часто записывается в виде Sn = u1 + u2 + … + un Если существует конечный предел Если Пример 1. Написать первые четыре члена ряда с общим членом Решение. Полагая в формуле для общего члена n =1,2,3,4, получаем:
Итак, Пример 2. Написать первые четыре члена ряда, общий член которого задан формулой Решение. Полагая в данной формуле n = 1,2,3,4,5,6, получаем
Таким образом, данный ряд можно записать так:
Пример 3. Найти формулу для общего члена ряда:
Решение. Можно заметить, что члены ряда – дроби, числитель каждой из которых равен единице (первый член тоже можно представить так: Далее, так как члены ряда имеют чередующиеся знаки, нужно ввести множитель вида Замечание 1. Перечисление членов ряда не всегда может начинаться при n= 1. Часто первым является член ряда с номером n= 0 или, например, n= 2. В таком случае и записывают ряд в виде Замечание 2. В формулах общего члена различных числовых рядов достаточно часто встречается знак факториала: n!=1×2×3×4×…×(n -1)× n. В частности, 1!=1, 2!=2, 3!=6 и т.д.; (n +1)!= n!×(n +1). Считается, что 0!=1. Иногда используют также знак двойного факториала четных и нечетных чисел: (2 n)!!=2×4×6×…×(2 n -2)(2 n). В частности, (2 n +2)!!=(2 n)!!×(2 n +2). (2 n +1)!!=1×3×5×…×(2 n -1)×(2 n +1). В частности, (2 n +3)!!=(2 n +1)!!×(2 n +3). Решить: Написать первые четыре члена ряда:
A 1) B 5) Написать простейшую формулу n -го члена ряда по указанным его первым членам и записать ряд, используя знак суммы (S): A 7) 10) B 12) 14)
При исследовании рядов основным вопросом является вопрос о сходимости и расходимости ряда. Непосредственное вычисление Следует отметить, что конечное число членов ряда влияет только на значение его суммы, но не на сам факт сходимости; таким образом, при исследовании ряда на сходимость мы можем, если нужно, отбросить первые несколько членов этого ряда.
Необходимый признак сходимости ряда (т.е. условие, при невыполнении которого ряд расходится): Если ряд Следствие: если общий член ряда не стремится к нулю при n→∞, то ряд расходится:
Указанный признак является необходимым, но недостаточным. Например, гармонический ряд: расходится, хотя
Пример 4. Исследовать вопрос о поведении ряда с помощью необходимого признака сходимости: Решение. Найдем предел общего члена ряда при n → ∞ (вспомним, что в этом случае можно пренебречь младшими слагаемыми (степенями n) в числителе и знаменателе): Данный ряд не удовлетворяет необходимому признаку сходимости и, следовательно, расходится. Пример 5. Проверить выполнимость необходимого признака сходимости для ряда Решение. Здесь Необходимое условие сходимости ряда выполняется; сделать из этого вывод о том, сходится ряд или расходится, нельзя.
Решить: A Проверить, выполняется ли необходимый признак сходимости для рядов: 1) 5)
Радикальный признак Коши. Если для ряда
Пример 1. Исследовать сходимость ряда Решение. Имеем
Так как
Пример 2. Доказать сходимость ряда Решение. Применим признак Коши. В данном случае Пример 3. Исследовать вопрос о сходимости ряда Решение. Применим признак Коши.
Пример 4. Исследовать на сходимость ряд Решение. Находим
Замечание При применении признака Коши следует учитывать, что
вообще,
Решить: Исследовать на сходимость с помощью радикального признака Коши: A 1) 5) B 9)
Интегральный признак Коши Пусть члены ряда Тогда ряд
Замечание. Нижним пределом интегрирования в интеграле может быть любое другое положительное число из области существования функции.
Пример 1. С помощью интегрального признака Коши доказать сходимость ряда Решение. Общий член данного ряда определяется формулой Рассмотрим несобственный интеграл
Предел существует и конечен, значит интеграл сходится и, следовательно, сходится и данный ряд.
Пример 2. Исследовать на сходимость ряд Решение. Общий член ряда определяется формулой находим функцию
Поскольку предел бесконечен, то интеграл расходится, поэтому расходится и данный ряд.
Пример 3. С помощью интегрального признака исследовать на сходимость ряд: Решение. Функция Рассмотрим несобственный интеграл
Поскольку предел равен конечному числу, а именно,
Пример 4. Доказать сходимость ряда Решение. Функция
Так как несобственный интеграл равен конечному числу, т.е. сходится, значит, и данный ряд сходится.
Замечание. Аналогичным образом рассматривается вопрос о сходимости ряда Дирихле с любым положительным значением р. Решить: Исследовать с помощью интегрального признака сходимость рядов: A 1) 4) Исследовать на сходимость: 7) 11) 15) 19)
До сих пор рассматривались ряды с положительными членами. Обратимся теперь к рядам, члены которых имеют разные знаки.
Знакопеременные ряды.
Ряд, содержащий как положительные, так и отрицательные члены, называется знакопеременным. При исследовании знакопеременного ряда
Если ряд Из расходимости ряда Если ряд Замечание. Если расходимость ряда из абсолютных величин установлена на основании необходимого признака сходимости, т.е. Ряд
Пример 1. Доказать сходимость ряда Решение. Составим ряд из абсолютных величин членов исследуемого ряда:
Рассмотрим ряд вида Ряд (2) является рядом Дирихле со значением р=3>1, следовательно, сходится. К ряду (1) применим признак сравнения: Таким образом, ряд, составленный из абсолютных величин членов заданного ряда сходится, следовательно, сам заданный ряд сходится абсолютно.
Ряд, у которого любые два соседних члена имеют разные знаки, называется знакочередующимся.
Признак Лейбница (сходимости знакочередующегося ряда) Знакочередующийся ряд сходится, если абсолютные величины его членов убывают, а общий член стремится к нулю, т.е. если выполняются следующие два условия: 1) Пример 2. Исследовать на сходимость ряд: Решение. Составим ряд из абсолютных величин членов данного ряда: Это гармонический ряд, который расходится. Следовательно, абсолютной сходимости в данном случае нет. Данный ряд является знакочередующимся. Проверим условия признака Лейбница: 1) очевидно, Следовательно, данный ряд сходится условно.
Пример 3. Исследовать на сходимость ряд Решение. Ряд из абсолютных величин членов данного ряда не удовлетворяет необходимому признаку сходимости:
Пример 4. Исследовать на сходимость ряд Решение. Исследуем ряд, составленный из абсолютных величин членов данного ряда:
Таким образом, ряд
Замечание. В случаях, аналогичных рассмотренной задаче, когда применение признака Лейбница связано с громоздкими выкладками, выгодно сразу же исследовать знакопеременный ряд на абсолютную сходимость с помощью признака Даламбера (или Коши). Отметим, что, если признак Даламбера (или Коши) устанавливает, что ряд, составленный из абсолютных величин членов заданного ряда, расходится, то, оказывается, заданный знакопеременный ряд не может сходиться даже условно, т.е. он расходится. Действительно, если, например,
Пример 5. Исследовать на сходимость: Решение: Рассмотрим ряд
В данном случае
Решить: Исследовать на сходимость знакопеременные ряды: A 1) 3) 6) 7) Степенные ряды.
Степенным ряд ом называется функциональный ряд вида
где
При
Основным свойством степенных рядов является следующее: Теорема Абеля: Если степенной ряд сходится при х=х0, то он будет сходиться (и притом абсолютно) при всяком значении х, удовлетворяющем неравенству ½ х-а ½ = ½ х0-а ½ Одним из следствий теоремы Абеля является факт существования для всякого степенного ряда интервала сходимости с центром в точке а: ½ х-а ½<R, или a -R< x<a +R, внутри которого степенной ряд абсолютно сходится и вне которого ряд расходится. На концах интервала (в точках x=a ±R) различные степенные ряды ведут себя по-разному: одни сходятся абсолютно на обоих концах; другие либо условно сходятся на обоих концах, либо на одном из них условно сходятся, на другом расходятся; третьи расходятся на обоих концах. Число R – половина длины интервала сходимости – называется радиусом сходимости степенного ряда. В частных случаях радиус сходимости ряда R может быть равен нулю или бесконечности. Если R=0, то любой степенной ряд сходится лишь при х=а. Если R=¥, то степенной ряд сходится на всей числовой оси. Одним из способов определения радиуса сходимости степенного ряда является применение признаков Даламбера и Коши. Радиус сходимости степенного ряда можно также вычислить по одной из формул
если соответствующий предел существует. Но эти формулы справедливы только для тех рядов, члены которых содержат все или почти все целые положительные степени х, т.е. в которых есть не более конечного числа нулевых коэффициентов.
Пример 1. Исследовать сходимость степенного ряда
Решение Здесь
Следовательно, ряд сходится для значений х, удовлетворяющих неравенству ½ х ½<1 или -1 <х< 1. Исследуем сходимость ряда на концах промежутка. Подставляя в данный ряд вместо х число 1, получим гармонический ряд Если х=-1, получаем числовой знакочередующийся ряд 1) Таким образом, данный ряд сходится при всех значениях х, удовлетворяющих неравенствам -1£х<1, и его промежуток сходимости представляет собой полузамкнутый интервал [-1;1). Геометрически это выглядит так:
Пример 2. Найти область сходимости ряда: Решение. Найдем радиус сходимости этого ряда по формуле
Следовательно, радиус сходимости
Теперь выясним поведение ряда на концах интервала сходимости. В правом конце, при х = Выше сходимость этого ряда была доказана при помощи интегрального признака. В левом конце, при х= - Таким образом, данный степенной ряд сходится в обоих концах интервала сходимости, значит, областью сходимости будет отрезок Графически:
Пример 3. Найтипромежутоксходимостиряда: Решение. Радиус сходимости ряда находим по формуле В нашей задаче Поэтому Значит, данный ряд сходится при значениях х, удовлетворяющих неравенству ½ х ½<10 или -10 <х< 10. Исследуем теперь поведение ряда на концах промежутка. Подставляя в данный ряд вместо х число 10 получаем ряд:
который расходится как гармонический (отличаясь от него лишь постоянным множителем) При х=-10 получим числовой знакочередующийся ряд:
Таким образом, данный степенной ряд сходится при всех значениях х, удовлетворяющих неравенствам -10£ х< 10, и его промежуток сходимости представляет собой полузамкнутый интервал [-10;10). Графически:
Пример 4. Найти радиус и интервал сходимости степенного ряда
Решение.
Радиус сходимости ряда равен нулю. Ряд сходится в единственной точке х =0 Замечание. 1. При вычислении предела использовали второй замечательный предел 2. Тот же результат можно получить и по формуле
Пример 5. Найти радиус и интервал сходимости степенного ряда Решение Так как то Пример 6. Найти промежуток сходимости ряда
Решение. Здесь мы не вправе применять формулу Данный ряд будет сходиться при всех значениях х, удовлетворяющих неравенству
Отсюда получаем Выражение в скобках не зависит от n, поэтому 2 х 2<1, или х 2<1/2. Окончательно получаем Исследуем поведение ряда на концах промежутка. При Таким образом, на концах интервала данный ряд расходится. Промежутком сходимости является интервал
Замечание. Тот же результат можно было получить, воспользовавшись радикальным признаком Коши. Пример 7 Найти область сходимости степенного ряда
Решение: Применим признак Даламбера. В данном случае
Ряд сходится при (х +3)2<1, т.е. ½ х +3½<1, -1 <х+ 3 < 1, т.е. -4 <х< -2. Исследуем сходимость ряда на концах промежутка (-4; -2). При х =-4 получаем ряд Следовательно, областью сходимости данного ряда является интервал (-4; -2).
Замечание. В некоторых случаях функциональный ряд можно при помощи замены переменой привести к виду степенного ряда, для нахождения области сходимости которого можно воспользоваться формулами радиуса сходимости.
Пример 8. Найти область сходимости степенного ряда
Решение. Поскольку данный ряд не содержит четных степеней х, формулами для нахождения радиуса сходимости пользоваться нельзя. Но это степенной ряд, поэтому он заведомо сходится при х=2 (в центре ряда). При любых других значениях х исследуемый ряд можно привести к виду
Таким образом, исследуемый ряд сходится при (х -2)2£1, т.е. ½ х -2½£1, т.е. 1£ х £3. Областью сходимости ряда является замкнутый промежуток [1;3].
Пример 9. Найти область сходимости ряда Решение. Сделаем замену переменной Таким образом, исследуемый ряд сходится при Область сходимости исследуемого ряда есть объединение двух лучей (-¥ -3] È (3; ¥). Графически:
Решить: Найти промежуток сходимости функционального ряда: A 1) 4) 6) 9) 12) B 15) (В последних задачах при подстановке граничных точек получаются числовые ряды, для исследования которых недостаточно приведенных в данном пособии признаков, так что эту часть решения выполнять не требуется)
B Вычисление сумм степенных и числовых рядов
Внутри области сходимости степенной ряд можно почленно дифференцировать и интегрировать, т.е. если
и Это позволяет во многих случаях вычислять сумму степенного ряда, учитывая, что сумма ряда бесконечно убывающей геометрической прогрессии вычисляется по формуле
Пример 1. Найти сумму ряда Решение: Обозначим
Полученный ряд является рядом геометрической прогрессии, причем
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 4031; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.244.201 (0.234 с.) |
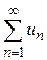 . Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:
. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда: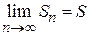 , то его называют суммой ряда и говорят, что ряд сходится.
, то его называют суммой ряда и говорят, что ряд сходится.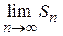 не существует (или равен бесконечности), то ряд суммы не имеет, т.е. расходится.
не существует (или равен бесконечности), то ряд суммы не имеет, т.е. расходится.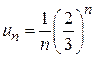 .
.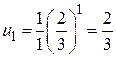 ;
; 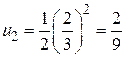 ;
; 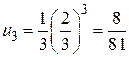 ;
; 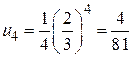
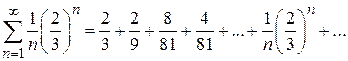
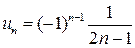 .
.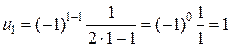 ;
; 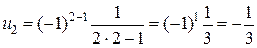 ;
;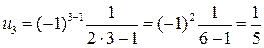 ;
; 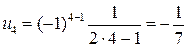 ;
;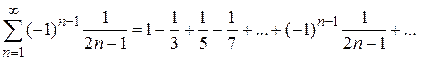
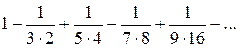 , считая, что каждый его член получается по тому закону, по которому образованы записанные члены.
, считая, что каждый его член получается по тому закону, по которому образованы записанные члены.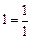 ), а знаменатель есть произведение нечётного числа на соответствующую степень числа 2 (для первого члена это тоже верно:
), а знаменатель есть произведение нечётного числа на соответствующую степень числа 2 (для первого члена это тоже верно: 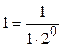 ).
).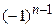 , чтобы получить искомую формулу:
, чтобы получить искомую формулу: 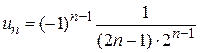 .
.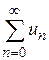 или
или 
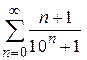 2)
2) 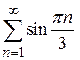 3)
3) 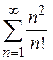 4)
4) 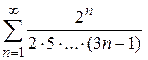
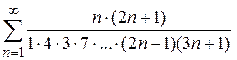 6)
6) 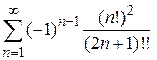
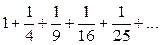 8)
8) 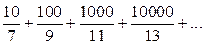 9)
9) 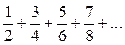
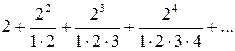 11)
11) 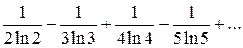
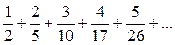 13)
13) 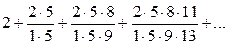
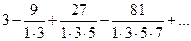 15)
15) 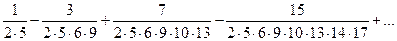
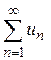 сходится, то его общий член стремится к нулю при неограниченном возрастании n, т.е.
сходится, то его общий член стремится к нулю при неограниченном возрастании n, т.е. 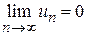
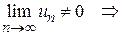
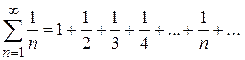
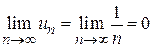 (расходимость гармонического ряда легко доказать с помощью интегрального признака – см. ниже)
(расходимость гармонического ряда легко доказать с помощью интегрального признака – см. ниже)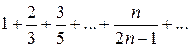
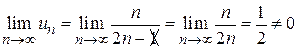
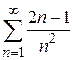
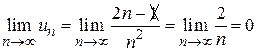 .
.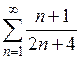 2)
2) 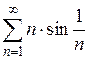 3)
3) 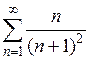 4)
4) 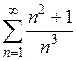
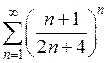 6)
6) 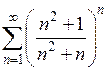 7)
7) 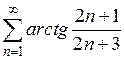 8)
8) 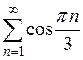
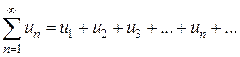 с положительными членами существует
с положительными членами существует 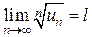 , то этот ряд сходится при l<1 и расходится при l>1. Если l=1, то вопрос о сходимости ряда остается открытым (нужны дополнительные исследования).
, то этот ряд сходится при l<1 и расходится при l>1. Если l=1, то вопрос о сходимости ряда остается открытым (нужны дополнительные исследования).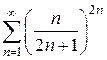
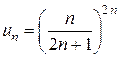 . Здесь удобно применить признак Коши:
. Здесь удобно применить признак Коши: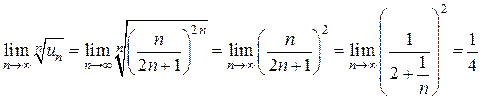 .
.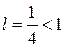 , то ряд сходится.
, то ряд сходится.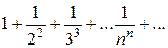
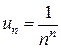 ; так как
; так как 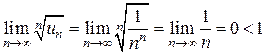 , то ряд сходится.
, то ряд сходится.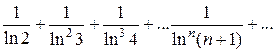
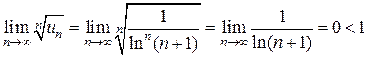 , следовательно, ряд сходится.
, следовательно, ряд сходится.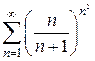 .
.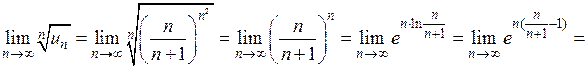
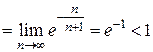 , следовательно, ряд сходится (по признаку Коши).
, следовательно, ряд сходится (по признаку Коши).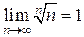 (см. тему «Предел функции);
(см. тему «Предел функции);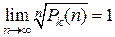 , где
, где 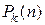 - многочлен
- многочлен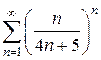 2)
2) 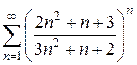 3)
3) 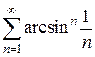 4)
4) 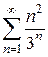
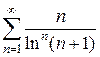 6)
6) 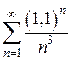 7)
7) 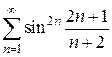 8)
8) 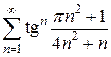
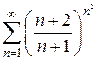 10)
10) 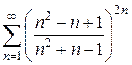 11)
11) 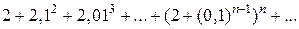
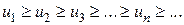 и пусть f(x) – такая непрерывная, положительная и невозрастающая функция, что f(1)=u1, f(2)=u2,…,f(n)=un,…
и пусть f(x) – такая непрерывная, положительная и невозрастающая функция, что f(1)=u1, f(2)=u2,…,f(n)=un,…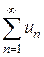 и несобственный интеграл
и несобственный интеграл 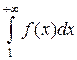 сходятся или расходятся одновременно (т.е. из сходимости интеграла следует сходимость ряда и наоборот).
сходятся или расходятся одновременно (т.е. из сходимости интеграла следует сходимость ряда и наоборот).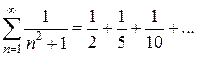
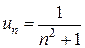 (n =1,2,3,…). Записав в этой формуле х вместо n, получаем функцию
(n =1,2,3,…). Записав в этой формуле х вместо n, получаем функцию 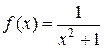 . Эта функция удовлетворяет условиям интегрального признака Коши (она принимает положительные значения и убывает с возрастанием х).
. Эта функция удовлетворяет условиям интегрального признака Коши (она принимает положительные значения и убывает с возрастанием х).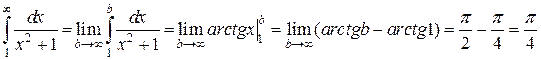 .
.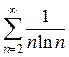
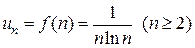 . (заметим, что суммирование начинается с n= 2, а при n =1 член ряда не определен, так как в знаменателе содержится множитель ln1=0; однако на исследование сходимости это не влияет). Из формулы общего члена ряда
. (заметим, что суммирование начинается с n= 2, а при n =1 член ряда не определен, так как в знаменателе содержится множитель ln1=0; однако на исследование сходимости это не влияет). Из формулы общего члена ряда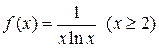 . Рассмотрим несобственный интеграл
. Рассмотрим несобственный интеграл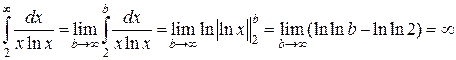 .
.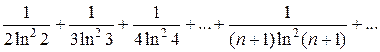
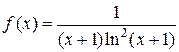 при х ³1 положительна, непрерывна и монотонно убывает, т.е. удовлетворяет условиям интегрального признака Коши.
при х ³1 положительна, непрерывна и монотонно убывает, т.е. удовлетворяет условиям интегрального признака Коши.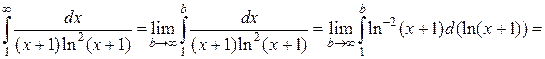
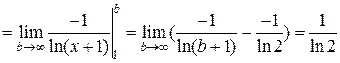 .
.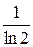 , то интеграл сходится, значит, и данный ряд также сходится.
, то интеграл сходится, значит, и данный ряд также сходится.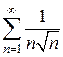
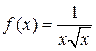 при х ≥1 положительна, непрерывна и монотонно убывает. Для применения интегрального признака следует рассмотреть несобственный интеграл
при х ≥1 положительна, непрерывна и монотонно убывает. Для применения интегрального признака следует рассмотреть несобственный интеграл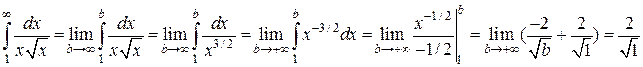 .
.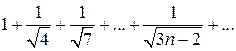 2)
2) 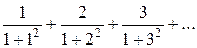 3)
3) 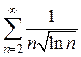
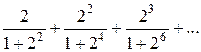 5)
5) 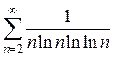 6)
6) 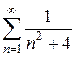
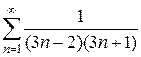 8)
8) 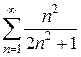 9)
9) 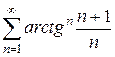 10)
10) 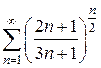
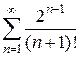 12)
12) 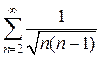 13)
13) 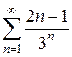 14)
14) 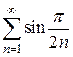
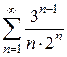 16)
16) 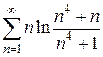 17)
17) 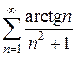 18)
18) 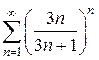
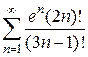 20)
20) 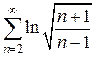 21)
21) 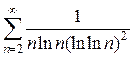
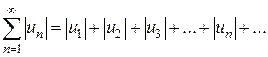
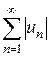 сходится, то сходится и сам ряд
сходится, то сходится и сам ряд 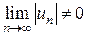 , то и исходный знакопеременный ряд будет расходиться, т.к. в этом случае и
, то и исходный знакопеременный ряд будет расходиться, т.к. в этом случае и 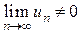 .
.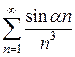 .
.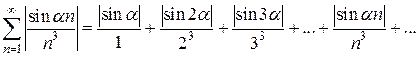 (1)
(1)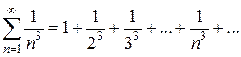 (2)
(2)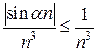 и (2) сходится Þ (1) сходится.
и (2) сходится Þ (1) сходится.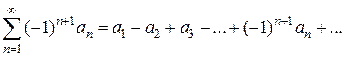
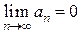 ; 2)
; 2) 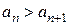 .
.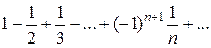
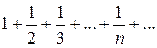
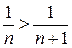 ; 2)
; 2) 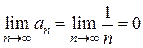 .
.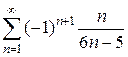
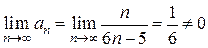 . Следовательно, данный ряд расходится.
. Следовательно, данный ряд расходится.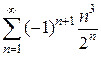
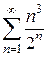 . Применяя признак Даламбера, имеем:
. Применяя признак Даламбера, имеем: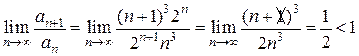 .
.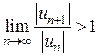 , то и
, то и 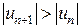 при n®¥, следовательно,
при n®¥, следовательно, 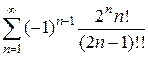
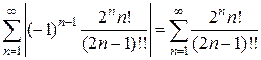 и составим отношение:
и составим отношение: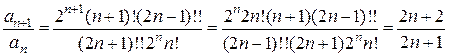 .
.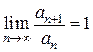 и признак Даламбера результата не дает. Но мы можем заметить, что для любых n верно, что
и признак Даламбера результата не дает. Но мы можем заметить, что для любых n верно, что 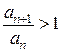 , то есть
, то есть 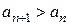 . Поскольку возрастающая положительная последовательность не может сходиться к нулю, то
. Поскольку возрастающая положительная последовательность не может сходиться к нулю, то 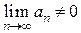 . Таким образом, необходимый признак не выполняется для ряда из абсолютных величин, а значит, и для данного знакочередующегося ряда. Следовательно, данный ряд расходится.
. Таким образом, необходимый признак не выполняется для ряда из абсолютных величин, а значит, и для данного знакочередующегося ряда. Следовательно, данный ряд расходится.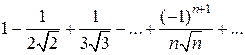 2)
2) 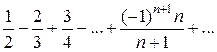
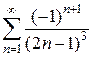 4)
4) 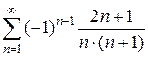 5)
5) 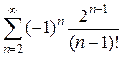
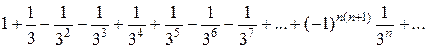
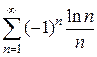 8)
8) 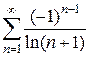 9)
9) 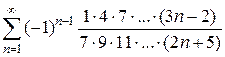
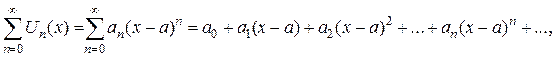
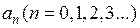 - числа, называемые коэффициентами ряда (некоторые из них могут быть нулями).
- числа, называемые коэффициентами ряда (некоторые из них могут быть нулями).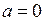 степенной ряд принимает вид
степенной ряд принимает вид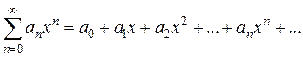
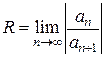 , (1)
, (1)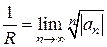 ,
,  (2)
(2)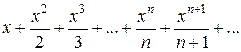
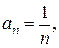
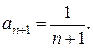 Найдем радиус сходимости ряда:
Найдем радиус сходимости ряда: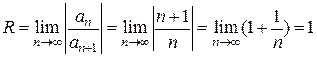
 , который, как известно, расходится.
, который, как известно, расходится.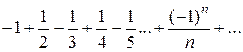 Этот ряд сходится, так как удовлетворяет условиям признака Лейбница:
Этот ряд сходится, так как удовлетворяет условиям признака Лейбница: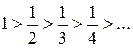 ; 2)
; 2) 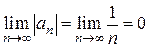 .
.
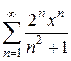
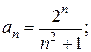
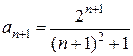 ;
; 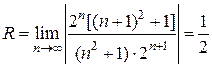
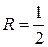 , а интервал сходимости (-
, а интервал сходимости (- 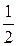 ;
; 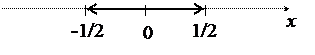
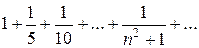
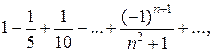 который сходится абсолютно, так как сходится соответствующий ряд из абсолютных величин:
который сходится абсолютно, так как сходится соответствующий ряд из абсолютных величин: 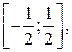 т.е.
т.е. 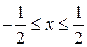 .
.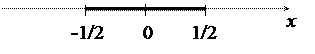
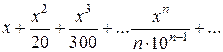
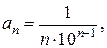
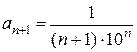
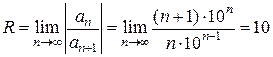 .
.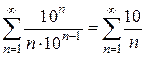 ,
,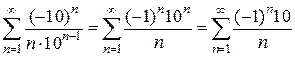 , который сходится условно.
, который сходится условно.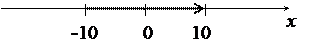
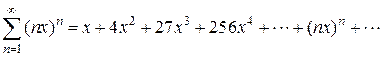
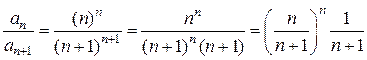 ;
;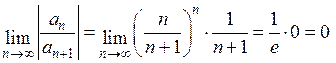
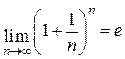 .
.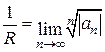 :
: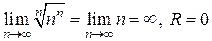 .
.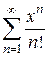 .
.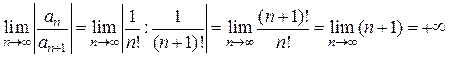 ,
,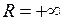 . Ряд сходится при всех х, т.е. в интервале (-¥; +¥).
. Ряд сходится при всех х, т.е. в интервале (-¥; +¥).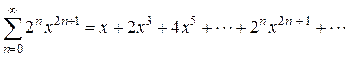
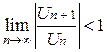 т.е.
т.е. 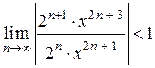 .
.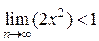 .
.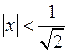 , т.е.
, т.е. 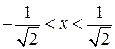 .
.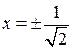 получим расходящийся числовой ряд 1+1+1+1+…+1+…
получим расходящийся числовой ряд 1+1+1+1+…+1+…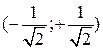 .
.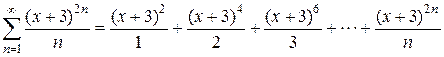 .
.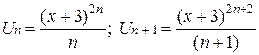 .
.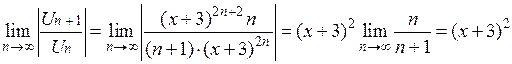
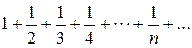 - гармонический ряд, который расходится. При х =-2 также получаем расходящийся гармонический ряд
- гармонический ряд, который расходится. При х =-2 также получаем расходящийся гармонический ряд 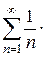
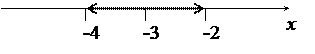
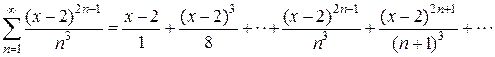 .
.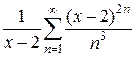 , поскольку х не зависит от n и, следовательно, общий множитель
, поскольку х не зависит от n и, следовательно, общий множитель 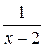 можно вынести за знак суммы. Сделаем замену переменной y =(x -2)2; тогда
можно вынести за знак суммы. Сделаем замену переменной y =(x -2)2; тогда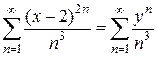 (y >0). Этот ряд сходится при y <R, где
(y >0). Этот ряд сходится при y <R, где 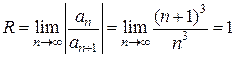 . При y =1 имеем ряд
. При y =1 имеем ряд 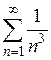 , который сходится как ряд Дирихле.
, который сходится как ряд Дирихле.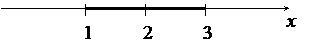
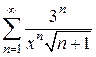 .
.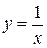 . Тогда задача сводится к исследованию сходимости степенного ряда
. Тогда задача сводится к исследованию сходимости степенного ряда 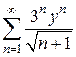 . Радиус сходимости найдем по формуле Коши:
. Радиус сходимости найдем по формуле Коши: 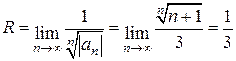 . При y=
. При y= 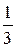 имеем ряд
имеем ряд 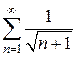 , который расходится как ряд Дирихле (р=1/2). При y=
, который расходится как ряд Дирихле (р=1/2). При y= 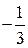 получаем знакочередующийся ряд
получаем знакочередующийся ряд 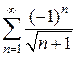 , который сходится (по признаку Лейбница).
, который сходится (по признаку Лейбница).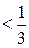 , т.е.
, т.е. 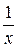
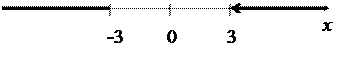
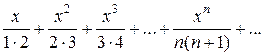 2)
2) 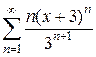 3)
3) 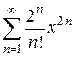 ;
;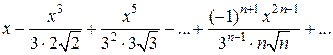 5)
5) 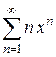
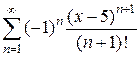 7)
7) 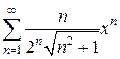 8)
8) 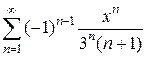
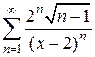 10)
10) 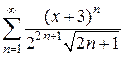 11)
11) 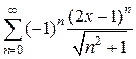
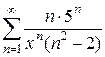 13)
13) 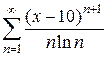 14)
14) 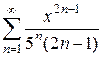
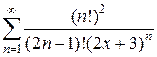 16)
16) 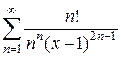
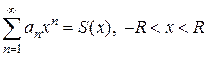 , то
, то 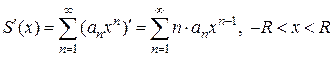
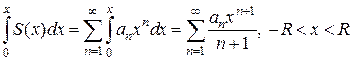 .
.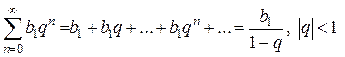 .
.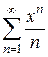
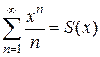 . Тогда внутри интервала сходимости данного ряда имеем:
. Тогда внутри интервала сходимости данного ряда имеем: