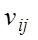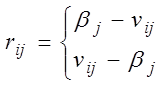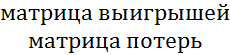Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о симметричной матричной игре
Матричная игра называется симметричной, если ее платежная матрица кососимметрическая Теорема: для симметричной матричной игры справедливы следующие утверждения: 1) Число m чистых стратегий игрока А совпадает с числом n чистых стратегий игрока В: m=n 2) Размерности векторов смешанных стратегий игроков А и В одинаковы 3) Множества SA смешанных стратегий игрока А совпадает с множеством SB смешанных стратегий игрока В: SA=SB 4) Симметричная матричная игра справедлива, т.е. ее цена V=0 5) Множество (SA)0 оптимальных стратегий игрока А совпадает с множеством (SB)0 оптимальных стратегий игрока В: (SA)0 = (SB)0
Теорема о сведении решения пары двойственных друг другу стандартных задач линейного программирования к решению матричной игры Рассмотрим вопрос о сведении решения любой пары взаимно двойственных задач линейного программирования к решению матричной симметричной игры. (матрица называется симметричной, если её платежная матрица кососимметрическая. Квадратная м-ца называется кососим-ской, если Решение следующей пары взаимно двойственных задач линейного программирования: 1. найти 2. найти эквивалентно решению симметричной матричной игры с матрицей
Точнее говоря, если
Основные понятия игры с природой. Матрица выигрышей сознательного игрока Во многих задачах финансово-экономической сферы принятие решения осложняется наличием неопределенности, заключающейся в неполноте информации об окружающей среде. Такую неопределенность могут порождать различные причины. Поэтому в таких задачах принятие решения зависит от реальных условий, которые называют в соответствующей математической модели «природой».
Саму же модель называют «игрой с природой». «Природа» может выступать как антагонистическая сторона, а может как кооперативная среда. Игру с природой можно определить как парную игру, в которой сознательный игрок А, заинтересованный в наиболее выгодном для него исходе игры, выступает против участника, совершенно безразличного к результату – природа (обозначим его П). Игра с природой — математическая модель ситуаций, когда осознанно действует только один игрок (обозначим его через А), принимающий решение, и когда исход игры зависит не только от решений игрока А, но и от состояния “природы” (обозначим через П), т. е. не от сознательно противодействующего противника, а от объективной, невраждебной действительности. Природа – это: 1. объективная действительность; 2. игрок, но не противник игрока А, потому что не действует осознанно против игрока А, а принимает неопределенным образом то или иное свое состояние, не преследуя конкретной цели и безразлично к результату игры. Статистик – игрок в игре с природой, действующий осознанно, т.е. лицо, принимающее решение (игрок А). Одним из важных предположений в теории игр с природой является предположение о том, что в любой момент времени природа П может находиться только в одном (но неизвестно, в каком) из n состояний П1, П2, …, Пn, то есть состояния природы разделены между собой во времени. Совокупность Для описания игры с природой необходимо также множество стратегий игрока A: Показателем благоприятности состояния Риском
Матрица рисков
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 927; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.204.201 (0.009 с.) |
 , т.е. если м-ца А равна своей транспонированной м-це с противоположным знаком:
, т.е. если м-ца А равна своей транспонированной м-це с противоположным знаком: 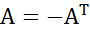 . Из этого следует, что косо-кая м-ца должна быть квадратной и все элементы её главной диагонали = 0).
. Из этого следует, что косо-кая м-ца должна быть квадратной и все элементы её главной диагонали = 0). при ограничениях xj ≥ 0, j=1,2,…,m;
при ограничениях xj ≥ 0, j=1,2,…,m;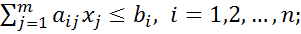
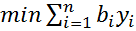 при ограничениях yi ≥ 0, i=1,2,…,n;
при ограничениях yi ≥ 0, i=1,2,…,n;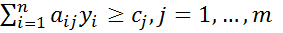
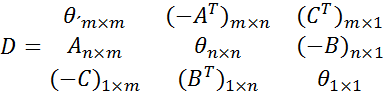 где
где 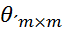 – квадратная нулевая матрица порядка m (все элементы – нули);
– квадратная нулевая матрица порядка m (все элементы – нули); 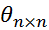 – квадратная нулевая матрица порядка n;
– квадратная нулевая матрица порядка n; 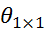 – квадратная нулевая матрица 1-го порядка, отождествляемая со своим единственным элементом – нулем;
– квадратная нулевая матрица 1-го порядка, отождествляемая со своим единственным элементом – нулем; и
и 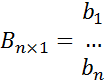 – соответственно матрица коэффициентов при неизвестных и вектор-столбец свободных членов системы ограничений в задаче пункта 1;
– соответственно матрица коэффициентов при неизвестных и вектор-столбец свободных членов системы ограничений в задаче пункта 1; 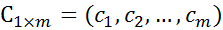 – вектор-строка коэффициентов при неизвестных целевой функции задачи пункта 1; АТ, ВТ, СТ – транспонированные матрицы.
– вектор-строка коэффициентов при неизвестных целевой функции задачи пункта 1; АТ, ВТ, СТ – транспонированные матрицы.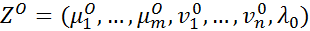 является оптимальной стратегией любого игрока в игре с матрицей D и
является оптимальной стратегией любого игрока в игре с матрицей D и 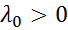 , то
, то 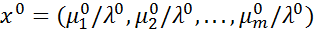 – оптимальное решение задачи пункта 1, а
– оптимальное решение задачи пункта 1, а  – оптимальное решение задачи пункта 2.
– оптимальное решение задачи пункта 2.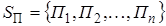 состояний природы П формируется либо на основе имеющегося опыта анализа состояний природы, либо в результате предположений и интуиции экспертов.
состояний природы П формируется либо на основе имеющегося опыта анализа состояний природы, либо в результате предположений и интуиции экспертов.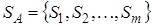 .
.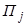 природы для увеличения выигрыша называется наибольший выигрыш при этом состоянии, т.е. наибольший элемент в j-м столбце матрицы игры:
природы для увеличения выигрыша называется наибольший выигрыш при этом состоянии, т.е. наибольший элемент в j-м столбце матрицы игры: 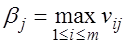 ,
, 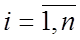 ,
, 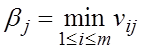
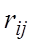 игрока A при выборе им стратегии
игрока A при выборе им стратегии 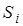 в условиях состояния
в условиях состояния 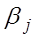 состояния природы
состояния природы 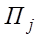 и выигрышем
и выигрышем