
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение наидлиннейшей возрастающей подпоследовательности
Дан массив из int d[MAXN], p[MAXN]; // константа MAXN равна наибольшему возможному значению n
for (int i=0; i<n; ++i) { d[i] = 1; p[i] = -1; for (int j=0; j<i; ++j) if (a[j] < a[i]) if (1 + d[j] > d[i]) { d[i] = 1 + d[j]; p[i] = j; } }
int ans = d[0], pos = 0; for (int i=0; i<n; ++i) if (d[i] > ans) { ans = d[i]; pos = i; } cout << ans << endl;
vector<int> path; while (pos!= -1) { path.push_back (pos); pos = p[pos]; } reverse (path.begin(), path.end()); for (int i=0; i<(int)path.size(); ++i) cout << path[i] << ' ';
28) Динамика по профилю. Задача "паркет" int n, m; vector < vector<long long> > d;
void calc (int x = 0, int y = 0, int mask = 0, int next_mask = 0) { if (x == n) return; if (y >= m) d[x+1][next_mask] += d[x][mask]; else { int my_mask = 1 << y; if (mask & my_mask) calc (x, y+1, mask, next_mask); else { calc (x, y+1, mask, next_mask | my_mask); if (y+1 < m &&! (mask & my_mask) &&! (mask & (my_mask << 1))) calc (x, y+2, mask, next_mask); } } }
int main() { cin >> n >> m;
d.resize (n+1, vector<long long> (1<<m)); d[0][0] = 1; for (int x=0; x<n; ++x) for (int mask=0; mask<(1<<m); ++mask) calc (x, 0, mask, 0);
cout << d[n][0];
}
Нахождение наибольшей нулевой подматрицы Дана матрица int n, m; cin >> n >> m; vector < vector<int> > a (n, vector<int> (m)); for (int i=0; i<n; ++i) for (int j=0; j<m; ++j) cin >> a[i][j];
int ans = 0; vector<int> d (m, -1), d1 (m), d2 (m); stack<int> st; for (int i=0; i<n; ++i) { for (int j=0; j<m; ++j) if (a[i][j] == 1) d[j] = i; while (!st.empty()) st.pop(); for (int j=0; j<m; ++j) { while (!st.empty() && d[st.top()] <= d[j]) st.pop(); d1[j] = st.empty()? -1: st.top(); st.push (j); } while (!st.empty()) st.pop(); for (int j=m-1; j>=0; --j) { while (!st.empty() && d[st.top()] <= d[j]) st.pop(); d2[j] = st.empty()? m: st.top(); st.push (j); } for (int j=0; j<m; ++j) ans = max (ans, (i - d[j]) * (d2[j] - d1[j] - 1)); }
cout << ans;
30) Гаусс const double EPS = 1E-9; int n; vector < vector<double> > a (n, vector<double> (n)); ... чтение n и a...
double det = 1; for (int i=0; i<n; ++i) { int k = i; for (int j=i+1; j<n; ++j) if (abs (a[j][i]) > abs (a[k][i])) k = j; if (abs (a[k][i]) < EPS) { det = 0; break; } swap (a[i], a[k]); if (i!= k) det = -det; det *= a[i][i]; for (int j=i+1; j<n; ++j) a[i][j] /= a[i][i]; for (int j=0; j<n; ++j) if (j!= i && abs (a[j][i]) > EPS) for (int k=i+1; k<n; ++k) a[j][k] -= a[i][k] * a[j][i]; }
cout << det;
Интеграл по формуле Симпсона
Биномиальные коэффициенты Биномиальным коэффициентом
int C (int n, int k) { double res = 1; for (int i=1; i<=k; ++i) res = res * (n-k+i) / i; return (int) (res + 0.01); }
Числа Каталана Числа Каталана — числовая последовательность, встречающаяся в удивительном числе комбинаторных задач. Первые несколько чисел Каталана
Числа Каталана встречаются в большом количестве задач комбинаторики. Количество корректных скобочных последовательностей, состоящих из Количество корневых бинарных деревьев с Количество способов полностью разделить скобками Количество триангуляций выпуклого Количество способов соединить Количество неизоморфных полных бинарных деревьев с Количество монотонных путей из точки Количество перестановок длины Количество непрерывных разбиений множества из Количество способов покрыть лесенку Вычисление Имеется две формулы для чисел Каталана: рекуррентная и аналитическая. Поскольку мы считаем, что все приведённые выше задачи эквивалентны, то для доказательства формул мы будем выбирать ту задачу, с помощью которой это сделать проще всего. Рекуррентная формула
Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях. Самой левой открывающей скобке l соответствует определённая закрывающая скобка r, которая разбивает формулу две части, каждая из которых в свою очередь является правильной скобочной последовательностью. Поэтому, если мы обозначим
Аналитическая формула
(здесь через Эту формулу проще всего вывести из задачи о монотонных путях. Общее количество монотонных путей в решётке размером
Ожерелья Задача "ожерелья" — это одна из классических комбинаторных задач. Требуется посчитать количество различных ожерелий из Решение Решить эту задачу можно, используя лемму Бернсайда и теорему Пойа. [ Ниже идёт копия текста из этой статьи ] В этой задаче мы можем сразу найти группу инвариантных перестановок. Очевидно, она будет состоять из
Найдём явную формулу для вычисления Подставляя найденные значения в теорему Пойа, получаем решение:
Можно оставить формулу в таком виде, а можно её свернуть ещё больше. Перейдём от суммы по всем
где
Задача о ферзях int SIZE = 0; int board[13][13]; int results_count = 0; void showBoard() { for(int a = 0; a < SIZE; ++a) { for(int b = 0; b < SIZE; ++b) { std::cout << ((board[a][b])? "Q ": ". "); } std::cout << '\n'; } } bool tryQueen(int a, int b) { for(int i = 0; i < a; ++i)
{ if(board[i][b]) { return false; } }
for(int i = 1; i <= a && b-i >= 0; ++i) { if(board[a-i][b-i]) { return false; } }
for(int i = 1; i <= a && b+i < SIZE; i++) { if(board[a-i][b+i]) { return false; } }
return true; }
void setQueen(int a) { if(a == SIZE) {
results_count++; return; }
for(int i = 0; i < SIZE; ++i) { if(tryQueen(a, i)) { board[a][i] = 1; setQueen(a+1); board[a][i] = 0; } }
return; }
int main() {
std::cin >> SIZE; setQueen(0); std::cout << results_count << std::endl;
return 0; }
36)Ханойские башни void hanoi_towers(int quantity, int from, int to, int buf_peg) { if (quantity!= 0) cout << from << ' ' << to << endl; hanoi_towers(quantity-1, buf_peg, to, from); int main() hanoi_towers(plate_quantity, start_peg, destination_peg, buffer_peg);
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.198 (0.077 с.) |
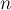 чисел:
чисел:  . Требуется найти в этой последовательности строго возрастающую подпоследовательность наибольшей длины.
. Требуется найти в этой последовательности строго возрастающую подпоследовательность наибольшей длины. размером
размером  . Требуется найти в ней такую подматрицу, состоящую только из нулей, и среди всех таких — имеющую наибольшую площадь (подматрица — это прямоугольная область матрицы).
. Требуется найти в ней такую подматрицу, состоящую только из нулей, и среди всех таких — имеющую наибольшую площадь (подматрица — это прямоугольная область матрицы). называется количество способов выбрать набор
называется количество способов выбрать набор  предметов из
предметов из  (начиная с нулевого):
(начиная с нулевого):
 листьями (вершины не пронумерованы).
листьями (вершины не пронумерованы). -угольника (т.е. количество разбиений многоугольника непересекающимися диагоналями на треугольники).
-угольника (т.е. количество разбиений многоугольника непересекающимися диагоналями на треугольники). точек на окружности
точек на окружности 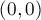 в точку
в точку  в квадратной решётке размером
в квадратной решётке размером  , не поднимающихся над главной диагональю.
, не поднимающихся над главной диагональю. , что
, что  ).
). с помощью
с помощью 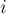 -ый из которых имеет высоту
-ый из которых имеет высоту 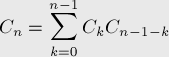
 , то для любого фиксированного
, то для любого фиксированного  будет ровно
будет ровно  способов. Суммируя это по всем допустимым
способов. Суммируя это по всем допустимым 
 . Теперь посчитаем количество монотонных путей, пересекающих диагональ. Рассмотрим какой-либо из таких путей, и найдём первое ребро, которое стоит выше диагонали. Отразим относительно диагонали весь путь, идущий после этого ребра. В результате получим монотонный путь в решётке
. Теперь посчитаем количество монотонных путей, пересекающих диагональ. Рассмотрим какой-либо из таких путей, и найдём первое ребро, которое стоит выше диагонали. Отразим относительно диагонали весь путь, идущий после этого ребра. В результате получим монотонный путь в решётке  . Но, с другой стороны, любой монотонный путь в решётке
. Но, с другой стороны, любой монотонный путь в решётке  . В результате получаем формулу:
. В результате получаем формулу:





 . Во-первых, заметим, что перестановки имеют такой вид, что в
. Во-первых, заметим, что перестановки имеют такой вид, что в  -ой позиции стоит
-ой позиции стоит 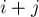 (взятое по модулю
(взятое по модулю  ,
,  ,
,  , и т.д., пока не придём в число
, и т.д., пока не придём в число  ; для остальных элементов выполняются похожие утверждения. Отсюда можно понять, что все циклы имеют одинаковую длину, равную
; для остальных элементов выполняются похожие утверждения. Отсюда можно понять, что все циклы имеют одинаковую длину, равную  , т.е.
, т.е.  ("gcd" — наибольший общий делитель, "lcm" — наименьшее общее кратное). Тогда количество циклов в
("gcd" — наибольший общий делитель, "lcm" — наименьшее общее кратное). Тогда количество циклов в  .
.
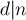 его слагаемое
его слагаемое  учтётся несколько раз, т.е. сумму можно представить в таком виде:
учтётся несколько раз, т.е. сумму можно представить в таком виде: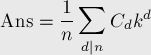
 — это количество таких чисел
— это количество таких чисел 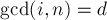 . Найдём явное выражение для этого количества. Любое такое число
. Найдём явное выражение для этого количества. Любое такое число  , где
, где  (иначе было бы
(иначе было бы  ). Вспоминая функцию Эйлера, мы находим, что количество таких
). Вспоминая функцию Эйлера, мы находим, что количество таких  . Таким образом,
. Таким образом,  , и окончательно получаем формулу:
, и окончательно получаем формулу:



