
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение цепочки перемещений
По новому плану перевозки грузов рассчитываем транспортную работу, которая будет равна Р = 30∙9 + 20∙5 + 30∙8 + 50∙9 + 20∙22 + 20∙10=1700 т∙км. План улучшился, однако полученный план не оптимален, поэтому его улучшение продолжается аналогичным способом. В заключение рассмотрим способ уменьшения числа занятых клеток, когда критерий m+n-1 нарушается в большую сторону(т.е. имеются лишние занятые клетки). Это приводит к тому, что индексы U и V определяются неоднозначно. Эта операция выполняется аналогично способу улучшения плана: - в матрице строится замкнутая цепочка из горизонтальных и вертикальных линий, вершины которой находятся в занятых клетках; - на вершинах цепочки, начиная с клетки с наименьшей загрузкой, ставят знаки (-) и (+); - нагрузку в клетках (-) уменьшают, а в клетках (+) увеличивают на величину наименьшей из них. Рассмотрим пример. Таблица 5 Матрица вычислений
В таблице 5 - семь занятых клеток, вместо необходимых шести (m+n-1=3+4-1=6). Наличие лишней занятой клетки приводит к тому, что индексы определяются неоднозначно. В самом деле, примем U1=0. Тогда согласно правилу (5) V2=15, V3=5, V4=8. Теперь индекс U2 можно найти либо из равенства U2=l22- V2, либо из равенства U2=l23- V3. В первом случае U2=9-15=-6, во втором - U2=6-5=l. Уменьшение числа занятых клеток производится следующим образом. В матрице строят замкнутую цепочку из горизонтальных и вертикальных отрезков так, чтобы все её вершины находились в занятых клетках (см. табл.5). Такая цепочка в матрице с числом занятых клеток более m+n-1 всегда имеется. На вершинах цепочки, начиная с клетки, имеющей наименьшую загрузку, расставляют попеременно знаки минус и плюс, после чего загрузки со знаком минус уменьшают, а со знаком плюс увеличивают на величину наименьшей из них. В результате число занятых клеток уменьшится не менее, чем на одну (табл.6). При необходимости данную процедуру повторяют столько раз, сколько это необходимо для получения m+n-1 занятых клеток. Таблица 6 Матрица вычислений
Приведём пример расчёта транспортной задачи по сокращению дальности перевозок грузов. Имеются 4 пункта отправления А1-А4 и 6 пунктов назначения В1-Вб. Конкретные значения величины грузов сведены в матрицу (табл.7).
Таблица 7
Матрица вычислений
1. Планируем, перевозки и заносим в матрицу. Затем вычисляем транспортную работу по допустимому исходному плану.
2. Проверяем число занятых клеток по индексу m+n-1. должно быть 4+6-1=9 имеется 8. Так как занятых клеток не хватает, то добавляем в клетку А1В1, объём 0т (выбор клетки происходит из логического анализа). 3.Вычисляем по критерию U+V=L индексы U1 - U4 и V1-V6. Для клетки A1B1 индекс U1=0.
4. Исследуем допустимый исходный план на оптимальность, сравнивая во всех принятых клетках расстояния и индексы L≥U+V. Можно видеть, что план не оптимален, так как критерию не удовлетворяют пять клеток А1В2, А3В2, А3В5, А3В6, А4В3. А4В5. Превышения записываем в кружочек. Клеткой с наибольшим потенциалом является А4В5. 5. Для клетки А4В5 строим цепочку перемещений, как показано в таблице 7, и получаем новый допустимый план. Рассчитываем транспортную работу по новому плану. Р=20∙4+25∙7+5∙9+10∙7+15∙6+15∙8+5∙12+15∙5=715 т∙км. План улучшился, так как транспортная работа уменьшилась с 805 т∙км до 715 т∙км. 6. Поскольку план не оптимален, строим новую цепочку перемещений (пунктирная линия). Рассчитываем новую транспортную работу. Р=20∙4+25∙7+5∙10+10∙7+15∙6+20∙8+15∙5=700т∙км. Планирование перевозок мелкопартионных грузов Задачи с нарушенным балансом производства и потреблениячасто встречаются в практике и называются задачами "открытого типа". Решать эти задачи методом потенциалов нельзя, так как в условия задачи входят неравенства. Такие задачи путем несложных преобразований приводятся к закрытой транспортной модели и решаются также методом потенциалов. 1-й случай - у поставщиков (пункты А1, A2...Ai,...Am) груза больше, чем требуется получателям В1 В2...Bj...Bm.
Расстояния между пунктами отправления и назначения составляют 1ij километров. Требуется составить такой план перевозок грузов, который обеспечит удовлетворение всех запросов потребителей при минимальной транспортной работе. Обозначим через х ijколичество тонн груза, планируемого к перевозке из пункта Аi, в пункт Вj. Тогда условия задачи записываются следующим образом: определить значения переменных х ij,минимизирующих транспортную работу,
при условиях
Равенство (7) гарантирует полное удовлетворение запросов каждого потребителя. Неравенство (8) выражает тот факт, что из каждого пункта отправления вывозится груза не больше того, что там имеется. Модель (6) — (9) отличается от закрытой транспортной модели наличием в условиях задачи неравенства (8). Подобные модели называют открытыми. Решить их непосредственно методом потенциалов нельзя, однако путём несложных преобразований рассматриваемая задача приводится к закрытой транспортной модели. Производят это путём введения фиктивного потребителя Вn+1 с объёмом потребления
Рассмотрим конкретную задачу, данные которой представлены в таблице 8. Таблица 8 Матрица условий
Требуется закрепить потребителей за поставщиками так, чтобы суммарная транспортная работа при перевозке была минимальной, а каждый потребитель получил нужное количество продукции. Составим матрицу условий, введя в неё фиктивный показатель Вф с потребностью равной (50+100+70) - (30+70+40+30) = 50 тонн. Выполнив уже известные нам вычисления, получаем оптимальный план перевозок груза и размещение невывезенного остатка на складах (табл.8). В нашем случае 50 т груза остаётся на складе А3. 2-й случай - у поставщиков груза меньше, чем нужно потребителю. В этом случае в матрицу вводится фиктивный поставщик Аф с запасом груза, выравнивающий дисбаланс. И далее задача решается так же, как и в первом случае. Транспортная задача с запретами имеет место, когда у поставщиков имеются разные грузы (например, речной песок и горный песок) и разным потребителям требуются разные грузы (например, только речной песок, только горный песок или любой песок). Требуется составить план перевозок и закрепить потребителей за поставщиками так, чтобы транспортная работа была минимальной. Решение задачи осуществляется методом потенциалов на матрице табл.1 и 2. но в клетках, соответствующих запрещённым перевозкам, записывают значения расстояний, значительно превышающих самые большие расстояния в матрице (т. е. запрещённые клетки блокируют). При решении такой матрицы гарантируется отсутствие нагрузок в блокированных клетках. Рассмотрим следующую задачу: на складах А1 и А2 имеется речной песок, а на складах А3 и А4 - горный песок в количествах соответственного, 20, 70 и 50 т. Потребителям В1 и В4 требуется только горный песок (запрещается возить речной песок из А1 и А2) в количествах соответственно 30 и 80 т, а остальным любой (либо горный, либо речной) в следующих размерах: В2-50т и В3- 40 т. Расстояния между пунктами приведены в таблице 9. Таблица 9 Расстояния между пунктами
План перевозок (закрепление потребителей за поставщиками) нужно составить так, чтобы потребители были удовлетворены полностью при минимальной транспортной работе. Решение транспортной задачи с запретами осуществляется методом потенциалов на матрице, в которой в клетках, соответствующих запрещённым перевозкам, вместо расстояний записывают произвольное число, значительно превышающее самое большое расстояние в матрице (клетки блокируют). При решении такой матрицы в оптимальном плане гарантируют отсутствие загрузок в блокируемых клетках. Так как абсолютная величина блокируемого числа безразлична (важно только, что оно значительно больше любого расстояния в таблице), в матрице его обозначают обычно буквой М (много). Под М понимают сколь угодно большое число, т. е. М=∞. При решении матрицы операции с числом М производят так же, как и с любым другим числом.
Матрицы условий и оптимальный план перевозок для данного примера представлены в таблице 10. Таблица 10 Матрица условий
Транспортная задача с минимальным временем перевозки (по критерию времени) имеет место, например, при транспортировке скоропортящихся грузов. Условия задачи также формулируются в виде матрицы (см. табл.1). Лимитирующей в данной задаче является самая длинная перевозка. Лучшим (оптимальным) будет являться план, у которого самая длительная перевозка будет иметь самую наименьшую длительность. Решение задачи сводится к последовательному решению методом потенциалов серии обычных транспортных задач, где оптимальное решение предыдущей служит исходным планом последующей задачи. Процедура вычислений складывается из следующих шагов. Шаг 1. Составить матрицу условий так. как это делают при решении обычной транспортной задачи. Шаг 2. Найти методом потенциалов план, у которого линейная форма
Шаг 3. Определить max t ij(наибольшее из времён) запланированных перевозок (где хij>0). Шаг 4. Во всех клетках матрицы, где tij>max Шаг 5. Отыскать для изменённой матрицы решение, при котором линейная форма Приведём пример. В таблице 11 приведена матрица условий задачи. Таблица 11 Матрица условий
В правом верхнем углу клеток записано время движения автомобилей между соответствующими пунктами в часах. Решив эту матрицу методом потенциалов, находим план (см. табл.11), обеспечивающий минимум оптимальности линейной формы (Т):
Наибольшее время перевозки по этому плану составляет 12 часов (перевозка из А1 в В4). Во всех клетках, где время доставки груза равно или больше этой величины (клетки А1В4 и А4В4), заменяем его числом М=100 (блокируем клетки) и вновь отыскиваем план, у которого линейная форма имеет наименьшую величину (табл.12).
Таблица 12 Матрица расчёта
Поскольку ни одна из загрузок не находится здесь в блокированной клетке (с числом 100), продолжаем вычисления. Теперь наибольшее время перевозки - 10 часов (клетка А4B1). Поэтому блокируем клетки A1B1 А3В4 и А4В1 у которых время равно 10 и находим новый план (табл.13) с минимальным значением линейной формы (10). Из таблицы видно, что здесь ни одна из загрузок не находится в блокированной клетке, поэтому процесс вычислений необходимо продолжить.
Таблица 13 План перевозок
Поскольку наибольшая продолжительность из планируемых перевозок равна 8 часам (клетки А2В4 и А4В3), блокируем клетки А2В4, А4В2 и А4В3, у которых время равно или больше 8 часов. В найденном новом плане (табл.14) с минимальным значением линейной формы две загрузки находятся в блокированных клетках. Это свидетельствует о том, что план перевозок, обеспечивающий доставку грузов всем потребителям за возможно короткое время, найден.
Таблица 14 Окончательный план перевозок
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.176 (0.034 с.) |





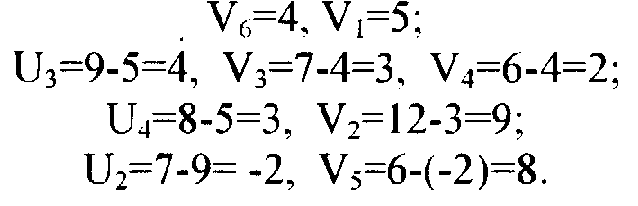


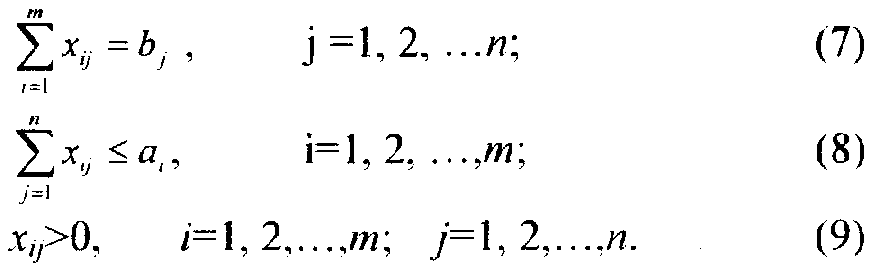
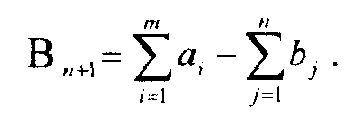



 достигает минимального значения.
достигает минимального значения. , заменить tij на число М =∞
, заменить tij на число М =∞ достигает минимума. Если в полученном решении х ij>0 расположены только в клетках, где tij <М, то снова находим max
достигает минимума. Если в полученном решении х ij>0 расположены только в клетках, где tij <М, то снова находим max  и повторяем шаги 4 и 5. Если же в полученном решении имеется хотя бы один хij>0, расположенный в клетке с tij =М, то оптимальным по критерию t(X)=max t ij(хij >0 - план перевозок, t(X) - время наиболее продолжительной перевозки) будет предыдущее решение. Очевидно, что после конечного числа повторений шагов 3, 4 и 5 будет получено оптимальное решение, т.е. такой план перевозок, по которому грузы всем потребителям будут доставлены за возможно короткое время.
и повторяем шаги 4 и 5. Если же в полученном решении имеется хотя бы один хij>0, расположенный в клетке с tij =М, то оптимальным по критерию t(X)=max t ij(хij >0 - план перевозок, t(X) - время наиболее продолжительной перевозки) будет предыдущее решение. Очевидно, что после конечного числа повторений шагов 3, 4 и 5 будет получено оптимальное решение, т.е. такой план перевозок, по которому грузы всем потребителям будут доставлены за возможно короткое время.
 . (10)
. (10)





