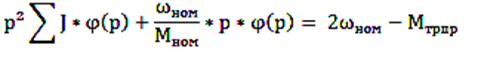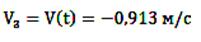Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения движения. Двухмассовая механическая система ⇐ ПредыдущаяСтр 3 из 3
Рис.3.1. Расчетная схема двухмассовой механической системы Расчетная схема двухмассовой системы. Система (рис. 3.1, а) содержит две вращающиеся массы с моментами инерции J1 и J2, связанные упругим звеном с жесткостью с. К первой массе (пусть это будет ротор двигателя) приложены моменты М, который примем пока постоянным, и Mc1, обусловленный, например, трением. Вторую массу будем полагать нагруженной статическим моментом Мс2. В статическом режиме, как отмечалось, все элементы системы будут двигаться с одинаковой скоростью, в динамическом же в силу наличия упругости скорости будут различны: ω1 – у первой массы и ω1 – у второй. Математическая модель. Поставим задачу – записать уравнения движения такой идеализированной двухмассовой системы. Расчленим систему на части (рис. 3.1, 6) и заменим каждую отброшенную часть ее реакцией, как это всегда делается в механике при составлении уравнений равновесия. Реакцию упругого элемента представим моментом упругого взаимодействия М12:
Для первой и второй масс на основании второго закона Ньютона записываем, соблюдая знаки моментов:
Уравнения (3.1) — (3.3) составляют полное математическое описание системы на рис. 3.1, а. Весь вопрос теперь в том, как распорядиться этим описанием, а это зависит от того, какие задачи нужно решать. Простые частные случаи. Пусть моменты сопротивления пренебрежимо малы
В коэффициенте перед третьей производной скорости легко узнать частоту собственных колебаний
а в правой части – среднее ускорение εср. Тогда окончательно будем иметь
Как и следовало ожидать, уравнение описывает незатухающий колебательный процесс (корни характеристического уравнения p1 = 0, p2,3 = ±jΩ12) с частотой колебаний Ω12. Оно определяет изменение средней скорости εсрt, на которую колебания накладываются. Решение уравнения (3.5) с учетом конкретных начальных условий дает полную картину движения первой массы. Так, при
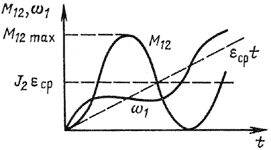
Зависимость ω1 от t показана на рис. 3.2.
Рис. 3.2. Динамические процессы в двухмассовой системе Динамические перегрузки. Математическое описание в виде (3.1) - (3.3) позволяет решать и другие задачи. Например, иногда очень важно оценить динамическую нагрузку упругого звена, т. е. найти и проанализировать зависимость М12 от времени. Решив исходные уравнения (3.1) - (3.3) относительно М12, получим
Это также уравнение незатухающего колебательного процесса, решение которого можно получить в виде
Зависимость M12(t) показана на рис. 3.2. Из нее следует, в частности, что в рассматриваемом случае максимальная нагрузка М12тах вдвое превышает среднюю, определяемую средним ускорением.
В них содержатся переменные (это все М и ω), параметры (с, J1 и J2) и оператор р, причем каждая переменная может быть выражена через другие переменные и параметры в сочетании с операторами. Уравнению (3.8), решенному относительно ω1, будет соответствовать, уравнению (3.7), решенному относительно M12,. Расчеты электромеханической системы. Выбираем реечный двигатель. Исходя из параметров двигателя выбираем: Диаметр вала = 0,003 м. Высота зуба = 0,002 м. Диаметр шестерни = 0,007 м. Рассчитываем коэффициент передачи: Скорость вращения номинальная:
Скорость вращения ведущей шестерни:
Коэффициент передачи:
Момент инерции:
Момент инерции приведения:
Момент трения:
Момент приведения трения:
Источник момента при использовании ИП генератора тока:
Результатом решения данного уравнения является:
В режиме источника напряжения:
Решение:
Учтем, что ω= ̇ и сделаем замену
По заданному графику движения груза рассчитываем:
Найдем время возврата в исходное состояние:
Примем время торможения равное 10% от t5-7, оно будет равно 1,5 сек. Рассчитаем скорость на стадии возврата в исходное состояние, учитывая, что оно будет отрицательным. Рассчитываем:
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.110.176 (0.013 с.) |

 (3.1)
(3.1) (3.2)
(3.2)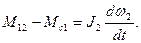 (3.3)
(3.3) и нас интересует движение первой массы. Преобразуем уравнения (3.1) - (3.3), сохранив ω1, и получим
и нас интересует движение первой массы. Преобразуем уравнения (3.1) - (3.3), сохранив ω1, и получим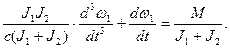
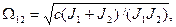 (3.4)
(3.4)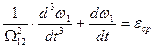 . (3.5)
. (3.5) имеем
имеем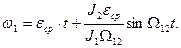
 . (3.6)
. (3.6)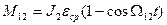 .
.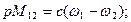 (3.7)
(3.7)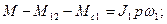 (3.8)
(3.8)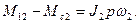 (3.9)
(3.9)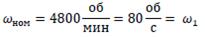

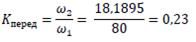
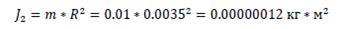
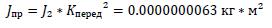
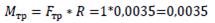
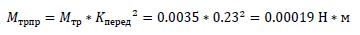
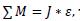 тогда получим равенство:
тогда получим равенство:
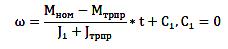

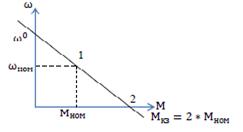
 учитывая, что ω = 2ωном, подставляем в равенство:
учитывая, что ω = 2ωном, подставляем в равенство: