
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательность независимых испытаний
(схема Бернулли) Предположим, что некоторый эксперимент можно проводить неоднократно при одних и тех же условиях. Пусть этот опыт производится n раз, т. е. проводится последовательность из n испытаний. Определение. Последовательность n испытаний называют взаимно независимой, если любое событие, связанное с данным испытанием, не зависит от любых событий, относящихся к остальным испытаниям. Допустим, что некоторое событие A может произойти с вероятностью p в результате одного испытанияили не произойти с вероятностью q= 1 -p. Определение. Последовательность из n испытаний образует схему Бернулли, если выполняются следующие условия: 1) последовательность n испытаний взаимно независима, 2) вероятность события A не изменяется от испытания к испытанию и не зависит от результата в других испытаниях. Событие A называют “ успехом” испытания, а противоположное событие
Для вычисления вероятности этого события справедлива формула Бернулли p ( где
Пример 1.16. Три раза подбрасывают кубик. Найти: а) вероятность того, что 6 очков выпадет два раза; б) вероятность того, что число шестерок не появится более двух раз. Решение. “Успехом” испытания будем считать выпадение на кубике грани с изображением 6 очков. а) Общее число испытаний – n =3, число “успехов” – m = 2. Вероятность “успеха” - p=
б) Обозначим через А событие, которое заключается в том, что грань с числом очков 6 появится не более двух раз. Тогда событие можно представить в виде суммы трех несовместных событий А= где В 30 – событие, когда интересующая грань ни разу не появится, В 31 - событие, когда интересующая грань появится один раз, В 32 - событие, когда интересующая грань появится два раза. По формуле Бернулли (1.6) найдем p (А) = р ( = Условная вероятность события Условная вероятность отражает влияние одного события на вероятность другого. Изменение условий, в которых проводится эксперимент, также влияет
на вероятность появления интересующего события. Определение. Пусть A и B – некоторые события, и вероятность p (B) > 0. Условной вероятностью события A при условии, что “событие B уже произошло” называется отношение вероятности произведения данных событий к вероятности события, которое произошло раньше, чем событие, вероятность которого требуется найти. Условная вероятность обозначается как p (A|B). Тогда по определению p (A | B)= Пример 1.17. Подбрасывают два кубика. Пространство элементарных событий состоит из упорядоченных пар чисел (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) (6,1) (6,2) (6,3) (6,4) (6,5) (6,6). В примере 1.16 было установлено, что событие A ={число очков на первом кубике > 4} и событие C ={сумма очков равна 8} зависимы. Составим отношение
Это отношение можно интерпретировать следующим образом. Допустим, что о результате первого бросания известно, что число очков на первом кубике > 4. Отсюда следует, что бросание второго кубика может привести к одному из 12 исходов, составляющих событие A: (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) (6,1) (6,2) (6,3) (6,4) (6,5) (6,6). При этом событию C могут соответствовать только два из них (5,3) (6,2). В этом случае вероятность события C будет равна Вероятность произведения событий Теорема умножения Вероятность произведения событий A 1 A 2 ¼An определяется формулой p (A 1 A 2 ¼An) = p (A 1) p (A 2 | A 1)) ¼p (An | A 1 A 2 ¼An- 1).(1.8) Для произведения двух событий отсюда следует, что p (AB) = p (A |B) p { B) = p (B |A) p { A). (1.9) Пример 1.18. В партии из 25 изделий 5 изделий бракованных. Последовательно наугад выбирают 3 изделия. Определить вероятность того, что все выбранные изделия бракованные. Решение. Обозначим события: A 1 = {первое изделие бракованное}, A 2 = {второе изделие бракованное}, A 3 = {третье изделие бракованное}, A = {все изделия бракованные}. Событие А есть произведение трех событий A = A 1 A2 A3. Из теоремы умножения (1.6) получим p (A) = р( A 1 A2 A3 ) =p (A 1) p (A 2 | A 1)) p (A 3 | A 1 A 2). Классическое определение вероятности позволяет найти p (A 1) – это отношение числа бракованных изделий к общему количеству изделий:
p (A 1) = p (A 2) – этоотношение числа бракованных изделий, оставшихся после изъятия одного, к общему числу оставшихся изделий: p (A 2 | A 1)) = p (A 3 ) – это отношение числа бракованных изделий, оставшихся после изъятия двух бракованных, к общему числу оставшихся изделий: p (A 3 | A 1 A 2) = Тогда вероятность события A будет равна p(A) =
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.33.107 (0.009 с.) |
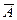 - “неудачей”. Рассмотрим событие
- “неудачей”. Рассмотрим событие ={ в n испытаниях произошло ровно m “успехов”}.
={ в n испытаниях произошло ровно m “успехов”}. ) =
) =  , m = 1, 2, …, n, (1.6)
, m = 1, 2, …, n, (1.6)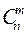 - число сочетаний из n элементов по m:
- число сочетаний из n элементов по m: =
=  .
.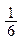 , а вероятность “неудачи” - q = 1 -
, а вероятность “неудачи” - q = 1 -  =
=  . Тогда по формуле Бернулли вероятность того, что результате трехразового бросания кубика два раза выпадет сторона с шестью очками, будет равна
. Тогда по формуле Бернулли вероятность того, что результате трехразового бросания кубика два раза выпадет сторона с шестью очками, будет равна .
. ,
, ) =
) =  +
+ 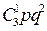 +
+  =
= .
. . (1.7)
. (1.7) .
. . Таким образом, информация о наступлении события A оказала влияние на вероятность события C.
. Таким образом, информация о наступлении события A оказала влияние на вероятность события C. ;
; ;
; .
. .
.


