Теорема существования и единственности решения дифференциального уравнения первого и второго порядков.

Теорема существования и единственности решения дифференциального уравнения первого и второго порядков.

Определение 1. Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную , искомую функцию и ее производную первого порядка , то есть

. (1) Если уравнение (1) можно разрешить относительно , то его записывают в виде

. (2) Обозначим через множество точек плоскости , на котором функция определена. Рассмотрим геометрический смысл уравнения (2). Производная функции представляет собой угловой коэффициент (тангенс угла наклона) касательной к кривой в точке с абсциссой . Следовательно, уравнение (2) устанавливает связь (зависимость) между координатами каждой точке плоскости и угловым коэффициентом касательной к интегральной кривой , проходящей через эту точку. Если указать это направление единичным вектором, проходящим через точку , то будет получено поле направлений.

Определение 2. Кривая, во всех точках которой направление поля одинаково, называется изоклиной.

Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить , то есть

Однородные уравнения.

Однородные уравнения – это уравнения вида k 0 xn + k 1 xn −1 y + k 2 xn −2 y 2+...+ kn −1 xyn −1+ knyn =0 k ​0​​ x ​ n ​​+ k ​1​​ x ​ n −1​​ y + k ​2​​ x ​ n −2​​ y ​2​​+...+ k ​ n −1​​ xy ​ n −1​​+ k ​ n ​​ y ​ n ​​=0 с двумя неизвестными, в каждом из слагаемых которых одинаковая сумма степеней этих неизвестных.

Линейные дифференциальные уравнения первого порядка.

Дифференциальное уравнение вида

y′+a(x)y=f(x),где a(x) и f(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка.

Уравнения Бернулли.

Оно записывается в виде y′+a(x)y=b(x)ym, где a(x) и b(x) − непрерывные функции. Если m=0, то уравнение Бернулли становится линейным дифференциальным уравнением.В случае когда m=1, уравнение преобразуется в уравнение с разделяющимися переменными. В общем случае, когда m≠0,1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки z=y1−m. Новое дифференциальное уравнение для функции z(x) имеет вид z′+(1−m)a(x)z=(1−m)b(x)

 

Уравнения в полных дифференциалах.

Дифференциальное уравнение вида P(x,y)dx+Q(x,y)dy=0 называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y)с непрерывными частными производными, что справедливо выражение du(x,y)=P(x,y)dx+Q(x,y)dy. Общее решение уравнения в полных дифференциалах определяется формулой u(x,y)=C, где C − произвольная постоянная.

Дифференциальные уравнения второго порядка, допускающие понижение порядка.

В общем случае дифференциальное уравнение второго порядка можно записать в виде F(x,y,y′,y′′)=0, где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y′′, то его можно представить в следующем явном виде:

y′′=f(x,y,y′). В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов: y′′=f(x),y′′=f(y),y′′=f(y′),y′′=f(x,y′),y′′=f(y,y′).

Однородные линейные дифференциальные уравнения второго порядка. Фундаментальная система решений. Теорема о структуре общего решения однородного линейного дифференциального уравнения второго порядка. Определитель Вронского.

Линейное однородное уравнение второго порядка с переменными коэффициентами записывается в виде y′′+a1(x)y′+a2(x)y=0, где a1(x) и a2(x) являются непрерывными функциями на отрезке [a,b].

Линейная независимость функций. Определитель Вронского Функции y1(x),y2(x),…,yn(x) называются линейно зависимыми на отрезке [a,b], если существуют постоянные α1,α2,…,αn, одновременное не равные нулю, такие, что для всех значений x из этого отрезка справедливо тождествоα1y1(x)+α2y2(x)+…+αnyn(x)≡0.Если же это тождество выполняется лишь при α1=α2=…=αn=0, то указанные функцииy1(x),y2(x),…,yn(x) называются линейно независимыми на отрезке [a,b]. Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функцииy1(x),y2(x) будут линейно независимыми на отрезке [a,b], если их отношение на данном отрезке тождественно не равно постоянной:y1(x)y2(x)≠const.В противном случае, при y1(x)y2(x)≡const, эти функции будут линейно зависимыми.
Пусть n функций y1(x),y2(x),…,yn(x) имеют производные (n−1) порядка. Определитель

W(x)=Wy1,y2,…,yn(x)=∣∣∣∣∣∣y1y′1…y(n−1)1y2y′2…y(n−1)2…………yny′n…y(n−1)n∣∣∣∣∣∣

называется определителем Вронского или вронскианом для указанной системы функций.
Теорема. Если система функций y1(x),y2(x),…,yn(x) линейна зависима на отрезке [a,b], то ее определитель Вронского тождественно равен нулю на этом отрезке. Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка [a,b], то функции y1(x),y2(x),…,yn(x) будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.

Теорема существования и единственности решения дифференциального уравнения первого и второго порядков.

Определение 1. Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную , искомую функцию 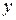и ее производную первого порядка 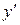, то есть

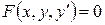. (1) Если уравнение (1) можно разрешить относительно , то его записывают в виде

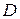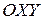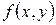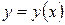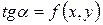. (2) Обозначим через множество точек плоскости , на котором функция определена. Рассмотрим геометрический смысл уравнения (2). Производная функции представляет собой угловой коэффициент (тангенс угла наклона) касательной к кривой в точке с абсциссой . Следовательно, уравнение (2) устанавливает связь (зависимость) между координатами каждой точке плоскости и угловым коэффициентом касательной к интегральной кривой , проходящей через эту точку. Если указать это направление единичным вектором, проходящим через точку , то будет получено поле направлений.

Определение 2. Кривая, во всех точках которой направление поля одинаково, называется изоклиной.

Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить , то есть