
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2). Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд? Решение: эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг. Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно. Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов). Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны. И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере. Пример. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек? Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5. Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5. БИЛЕТ 31 Число размещений без повторений из n по m (n различных элементов) вычисляется по формуле: Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в наборе не повторяются;
Решение. Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА. По формуле получаем: !!! Размещением из n элементов по m элементов без повторений называется упорядоченное подмножество попарно различных m элементов множества Mn ( БИЛЕТ 32 Размещениями с повторениями из n элементов по m называются упорядоченные m-элементные выборки, в которых элементы могут повторяться. Число размещений с повторениями вычисляется по формуле: Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 2) буквы могут повторяться? Решение. Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА. По формуле (3.2) получаем: !!! Размещение с повторениями или выборка с возвращением — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. БИЛЕТ 33. Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов). Число сочетаний без повторений (n различных элементов, взятых по m) вычисляется по формуле:
Число сочетаний c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться) вычисляется по формуле:
Пример. Возьмем буквы Б, А, Р. Какие сочетания из этих букв, взятых по две, можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) можно брать по два одинаковые буквы. Решение.
Получатся наборы: БА (БА и АБ - один и тот же набор), АР и РБ По формуле
Получатся наборы: ББ, БА, БР, АА, АР, РР. Поформуле
Пример. Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать? Решение. Надо выбрать двух человек из 20. Ясно, что от порядка выбора ничего не зависит, то есть Иванов-Петров или Петров-Иванов - это одна и та же пара дежурных. Следовательно, это будут сочетания из 20 по 2.
По формуле
Пример. В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 6 булок хлеба?
Решение. Обозначая булки белого и черного хлеба буквами Б и Ч, составим несколько выборок: ББББББ, ББЧЧББ, ЧЧЧЧЧБ,... Состав меняется от выборки к выборке, порядок элементов несущественен, значит это - сочетания с повторениями из 2 по 6. По формуле Cделаем проверку и выпишем все варианты покупки: ББББББ, БББББЧ, ББББЧЧ, БББЧЧЧ, ББЧЧЧЧ, БЧЧЧЧЧ, ЧЧЧЧЧЧ. Их действительно 7. Билет №8 Понятие разбиения множества на классы. Виды классификаций. Примеры. Опр: Говорят, что множество Х разбито на классы Х1, Х2, …, Хn, если выполняются 2 условия: 1)Классы попарно не пересекаются Х1 ÇХ2 Ç…Ç Хn = Æ 2)Объединение всех подмножеств совпадает с множеством Х Х1 È Х2 È … È Хn = Х Если хотя бы 1 из условий не выполняется, то данные разбиения на подмножества не являются разбиением на классы. Рассмотрим множество N, его элементы обладают разными свойствами, и выделим числа, которые обладают свойством «быть кратным 5». Это свойство выделяет в множестве N подмножества, в которых находятся числа, делящиеся на 5. Про остальные числа можно сказать, что они не делятся на 5. Получается 2 подмножества N, они не пересекаются, и их объединение – все мн-во N. При помощи 1-го св-ва мн-во разбивается на 2 класса: 1кл – обладает св-вом; 2кл – не обладает св-вом. Рассмотрим случай, когда для элементов мн-ва заданы 2 св-ва: 1 – «быть кратным 5» 2 – «быть кратным 3» В результате можно выделить 2 подмножества А – кратны 5 В – кратны 3 Множества А и В пересекаются, и в пересечении находятся числа, которые кратны 15, то для того, чтобы выделение данных свойств привело к разбиению на классы, необходимо выделить следующие подмножества: 1) – кратны 5, но не 3 2) – кратны 3, но не 5 3) – кратны и 3 и 5 4) – не кратны 3 и 5 Выделение 2-х св-в привело в разбиению на 4 класса. Рассмотрим 2 свойства натуральных чисел: 1 – быть кратным 3 2 – быть кратным 6 А – кратны 3 В – кратны 6 1)кратны 6 2) кратны 3, но не 6 3) не кратны 3 Выделение 2-х св-в привело к разбиению на 3кл.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.226.105 (0.011 с.) |

 наборов.
наборов. ).
).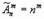
 наборов.
наборов.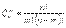

 получаем: наборов.
получаем: наборов. получаем: наборов.
получаем: наборов. получаем: способов.
получаем: способов. получаем способов.
получаем способов.


