Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра дизайна и технологииСтр 1 из 8Следующая ⇒
ПРАВИТЕЛЬСТВО МОСКВЫ МОСКОВСКИЙ КОМИТЕТ ОБРАЗОВАНИЯ МОСКОВСКИЙ ГОРОДСКОЙ ШДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ________________________________________________________ Кафедра дизайна и технологии
«ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЧЕРТЕЖА» Краткий конспект лекций по основным разделам начертательной геометрии
Для студентов факультета технологии и предпринимательства
Москва 2001 Теоретические основы построения чертежа. Краткий конспект лекций по основным разделам геометрии. // А.И. Шевцов, А.И. Родионов. – М.: Изд-во МПГУ, 2001. 48 с. В пособии содержатся сведения о предмете начертательной геометрии, в краткой форме изложены основные положения метода проекций, вводится понятие комплексного чертежа, дается краткий обзор геометрических образов. Основное внимание уделено теории и методам решения позиционных задач и метрических задач, рассматривается их классификация и алгоритмы решения типовых задач. Приводится краткие сведения о развертывании поверхностей и о методах построения развёрток. Пособие иллюстрировано достаточным количеством рисунков, поясняющих излагаемый теоретический материал. Предназначено для студентов специальности 03.06.00 «Технология и предпринимательство» Московского государственного педагогического университета, может быть полезно студентам и других специальностей при изучении курсов для начертательной геометрии, черчения, графики.
© Шевцов А.И., Родионов А.И., 2001 © Московский городской педагогический университет Обозначения Условимся обозначать: A, B,..., 1, 2,..., A1 В2,..., 13, 21,... - большими буквами латинского алфавита или цифрами (с индексами) точки и их проекции; a, b, d, …, а1 Ь2, d3,... - малыми буквами латинского алфавита (с индексами) - линии и их проекции (в том числе и прямые линии); Ф, Ψ, Σ,..., Ф1, Ψ2, Гз, Σ1,... - большими буквами греческого алфавита (с индексами) — плоскости и поверхности и их проекции. При записи решений примеров будем использовать следующие обозначения: m(m1; m2) - геометрический образ m задан его проекциями m1 и m2;
= - результат действия; => - следовательно; ┴ - перпендикулярно; ║ - параллельно;
≡ - тождественно совпадает;
╨ - проецирует (проецирующий образ);
Предварительные замечания Начертательная геометрия входит в число учебных предметов, составляющих основу инженерного образования. Предметом начертательной геометрии является изложение и обоснование способов построения изображений пространственных форм на плоскости и способов решения задач геометрического характера по заданным изображениям этих форм. Изображения, построенные по правилам, изучаемым в начертательной геометрии, позволяют мысленно представить форму предметов и их взаимное расположение в пространстве, исследовать геометрические свойства предметов.
Начертательная геометрия вызывает усиленную работу пространственного воображения, развивает его, является первым шагом на пути к курсу черчения, обеспечивая выразительность и точность чертежей. Правила построения изображений, излагаемые в начертательной геометрии, основаны на методе проекций. Рассмотрение этого метода начнем с построения проекций точки, поскольку любую плоскую или пространственную форму можно представить в виде некоторой совокупности точек.
Виды проецирования Для уяснения сущности метода начертательной геометрии обратимся к рис. 1.
Для изображения предметов на плоскости используют метод проецирования, который заключается в том, что луч SA (рис.1), выходя из точки S, пересекает плоскость П' в точке А'. Точка S называется центром проецирования, направление SA – проецирующим лучом, плоскость П' – плоскость проекций и А' – проекцией точки А на плоскость проекций П'. В зависимости от положения центра проецирования по отношению к плоскости проекций может быть: - центральным или коническим (если проецирующие лучи выходят из одной точки - центра проецирования S). - параллельным или цилиндрическим (когда все проецирующие лучи параллельны друг другу и какому-либо направлению). Параллельное проецирование можно рассматривать как частный случай центрального, если центр проецирования S удален в бесконечность.
В зависимости от направления проецирующих лучей по отношению к плоскости проекций параллельное проецирование может быть: - косоугольным (проецирующие лучи не перпендикулярны к плоскости проекций); - прямоугольным (проецирующие лучи перпендикулярны к плоскости проекций). Заметим, что во всех случаях проецирования проецируемый объект располагается между наблюдателем и выбранной плоскостью проекций. В основе выполнения всех чертежей лежит именно прямоугольное проецирование, поэтому в дальнейшем этот вид проецирования и будет рассматриваться.
Комплексный чертеж. Точка Проекционные изображения, используемые в технической документации, должны обладать следующими свойствами: - быть наглядными; - обладать простотой графического выполнения; - быть обратимыми, то есть такими, чтобы по ним можно было представить сам предмет и в дальнейшем его изготовить.
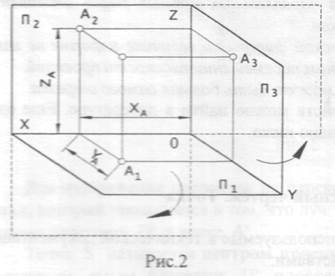
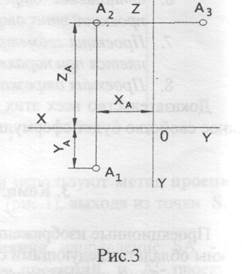
Наличие одной проекции создает неопределенность изображения. Поэтомув практике однопроекционные изображения дополняют. Одним из таких дополнений являются комплексные изображения. Они получаются, если предмет с помощью прямоугольного проецирования проецируют на три взаимно перпендикулярных плоскости проекции. Этот способ впервые был предложен, систематизирован и описан французским ученым Г.Монжем, поэтому его иногда называют методом Монжа. Три взаимно перпендикулярные плоскости, на которые производят проецирование какого-либо предмета или точки, дают три изображения, а также некоторую систему координат ОХУZ, где положение любой точки определяется однозначно, тремя её проекциями: А (ХА, YA, ZA). Обычно рассматривают предмет, расположенный в пространстве трех плоскостей, образующих так называемый "правый" угол. Вообще говоря, три плоскости П1-П2-П3 делят пространство на 8 частей (октантов). Здесь показан один октант, где все координаты точки А (ХА, УА, ZA) - положительны. Плоскости называют: П1 - горизонтальная плоскость проекций, П2 - фронтальная плоскость проекций, П3 - профильная плоскость проекций. В связи с этим проекции любой точки на эти плоскости снабжаются соответствующим индексом -1,2 или 3 (рис.2). Чтобы изображение предмета, спроецированное на три плоскости проекций, изобразить на одной плоскости, мысленно производят разрез по оси ОY и поворачивают плоскость П1 вокруг оси ОХ, а плоскость П3 - вокруг оси ОZ для совмещения с плоскостью П2, получая изображение показанное на рис. 3.
Линии А1А2 и А2А3 называют линиями проекционной связи (или просто линиями связи). У А1А2 ┴ X и А2А3 ┴ Z, поскольку проецирование прямоугольное. Основные свойства трсхпроекционного комплексного чертежа, приведенного на рис.3: - две проекции точки принадлежат одной линии связи; - линия связи перпендикулярна к соответствующей оси проекций; - две проекции тючки определяют ее третью проекцию. Таким образом, Комплексный чертеж - это изображение на одной плоскости нескольких взаимных прямоугольных проекций предмета, полученное после определенного совмещения плоскостей проекции с плоскостью чертежа. Двухпроекционный комплексный чертеж состоит из изображений предметов на двух, плоскостях проекций, совмещенных с плоскостью чертежа. Им удобно пользоваться, поскольку две любых проекции предмета или точки всегда содержат все три их координаты, однозначно определяющих положение предмета или точки в пространстве. Другими словами, и в этом случае чертеж будет обратимым. Следовательно, имея проекции какого-то предмета, можно однозначно представить его в натуре.
Чтобы закончить все о точке, отметим, что точки, лежащие на одном проецирующем луче, называются конкурирующими точками (это, например, точки А и К на рис. 1). Это обстоятельство лежит в основе метода конкурирующих точек, используемого для определения видимости проекций линий и плоских фигур. Линия Кинематическое определение линии может быть следующим: линия - это множество всех последовательных положений движущейся точки. Не вникая в классификацию всех существующих линий, выделим те, с спорыми в дальнейшем чаще всего придётся иметь дело: - прямые (движущаяся точка не изменяет направления своего движения); - ломаные (звенья ломаных - отрезки прямых); - замкнутые (движущаяся точка периодически возвращается в исходное положение); - разомкнутые (движущаяся точка не возвращается в исходное положение); - кривые (движущаяся точка изменяет направление своего движения); - плоские (все точки таких линий принадлежат одной плоскости); - пространственные (все точки их не принадлежат одной плоскости). алгебраические, трансцендентные, графические и т.д.). Прямую линию можно задать двумя точками. Как задавать одну точку и изображать её на комплексном чертеже, мы уже знаем. Задав так же вторую точку и соединив их отрезком, получим прямую, проекция которой на чертеже будет выглядеть так, как показано на рис.4, где отрезок АВ задает направление прямой (напомним, что сама прямая в пространстве бесконечна).
В зависимости от расположения той или иной прямой по отношению к плоскостям проекций различают прямые: - общего положения; - частного положения. Прямая общего положения - не параллельна и не перпендикулярна ни одной из плоскостей проекций. Примером такой прямой является изображенный отрезок прямой АВ. Прямые частного положения бывают следующими: - прямые уровня; - проецирующие прямые. Первые из них параллельны одной из плоскостей проекций, а вторые перпендикулярны одной из этих плоскостей. Этим и определяются их названия:
горизонталь - прямая, параллельная горизонтальной плоскости проекций (прямая горизонтального уровня). фронталь - прямая, параллельная фронтальной плоскости проекций (прямая фронтального уровня). профильная прямая - прямая, параллельная профильной плоскости проекций (прямая профильного уровня).
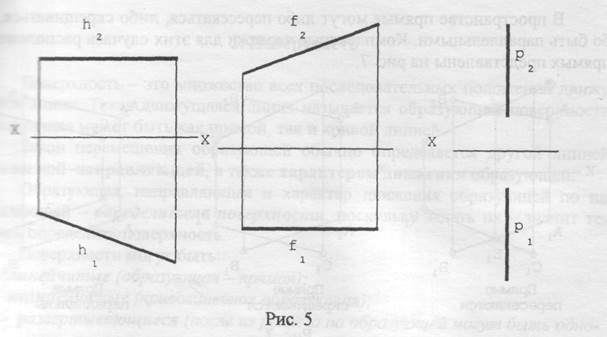
На чертеже они выглядят так как показано на рис. 5, где: h2 – фронтальная проекция горизонтали; h1 – горизонтальная проекция горизонтали; f2 - фронтальная проекция фронтали; f1 – горизонтальная проекция фронтали; p1, p2 – соответствующие проекции профильной прямой.
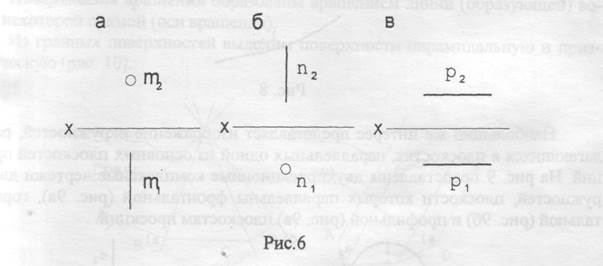
Поскольку проецирующая прямая перпендикулярна к какой-либо из плоскостей проекций, проекция прямой на ту плоскость проекций, к которой она перпендикулярна, представляет собой точку (главная проекция). Среди проецирующих прямых (рис. 6) различают: - фронтально-проецирующие (рис. 6а); - горизонтально-проецирующие (рис. 66); - профильно-проецирующие (рис. 6в).
Нужно заметить, что проецирующие прямые одновременно являются и прямыми уровня. Фронтально-проецирующая прямая, например, - одновременно и горизонталь, и профильная прямая, поскольку она параллельна и горизонтальной, и профильной плоскостям проекций. По этим же причинам горизонтально-проецирующая прямая - фронталь и профильная прямая, а профильно-проецирующая прямая - горизонталь и фронталь. То есть, проецирующие прямые одновременно являются дважды прямыми уровня.
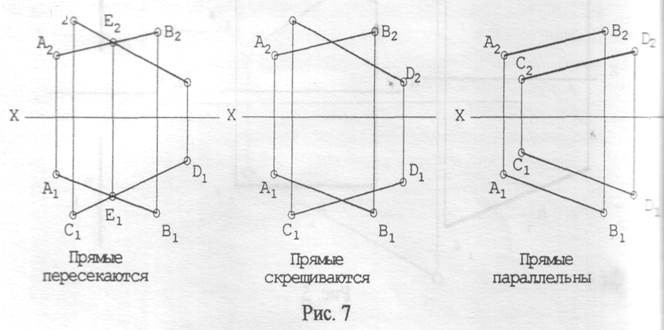
В пространстве прямые могут либо пересекаться, либо скрещиваться, либо быть параллельными. Комплексные чертежи для этих случаев расположения прямых представлены на рис. 7.
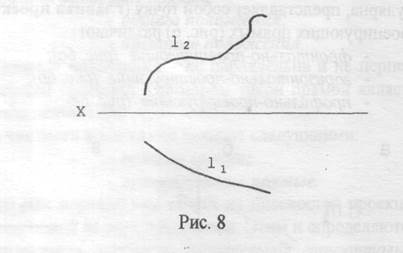
Кривая линия чаще всего может быть задана своими проекциями (рис. 8)
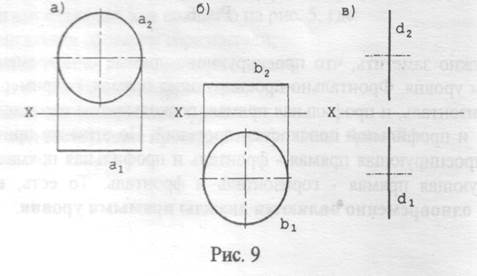
Наибольший же интерес представляет изображение окружностей, располагающихся в плоскостях, параллельных одной из основных плоскостей проекций. На рис. 9 представлены двухпроекционные комплексные чертежи для окружностей, плоскости которых параллельны фронтальной (рис. 9а), горизонтальной (рис. 9б) и профильной (рис. 9в) плоскостям проекций.
Поверхность
Поверхность - это множество всех последовательных положений движущейся линии. Такая движущаяся линия называется образующей поверхности. Образующая может быть как прямой, так и кривой линией. Закон перемещения образующей обычно определяется другой линией, называемой направляющей, а также характером движения образующей. Образующая, направляющая и характер движения образующей по направляющей - определитель поверхности, поскольку задать их - значит тем самым определить поверхность. Поверхности могут быть: - линейчатые (образующая — прямая); - нелинейчатые (криволинейная образующая); - развертывающиеся (после их разреза по образующей могут быть односторонне совмещены с плоскостью без разрывов и складок); - неразвёртывающиеся (если невозможно осуществить процедуру, описанную в предыдущем пункте).
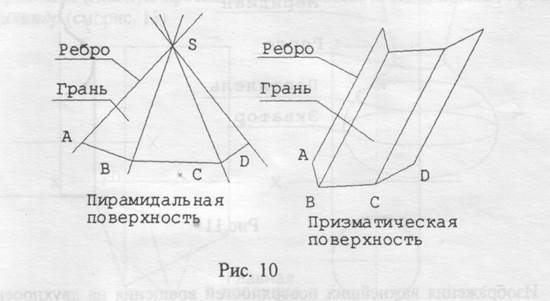
Особый вид поверхностей - поверхности: - гранные; - вращения. Гранные поверхности образовываются при движении прямолинейной образующей по ломанной направляющей. Поверхности вращения образованы вращением линии (образующей) вокруг некоторой прямой (оси вращения). Из гранных поверхностей выделим поверхности пирамидальную и призматическую (рис. 10).
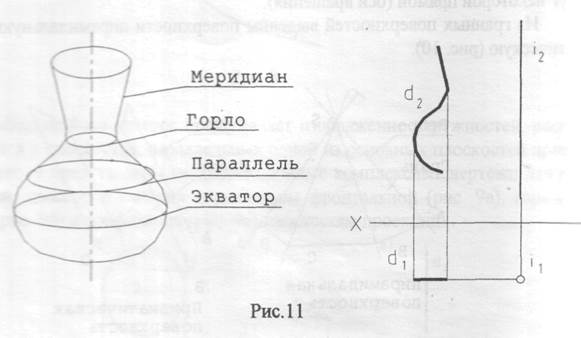
Из числа гранных поверхностей выделяют группу многогранников. Многогранник - замкнутая поверхность, образованная некоторым количеством граней. Важнейшими многогранниками являются пирамида и призма. Пирамида - многогранник, у которого одна грань (основание) представляет собой произвольный многоугольник, а остальные грани (боковые) - треугольники с общей точкой S, называемой вершиной. Если в основании пирамиды треугольник, пирамида называется треугольной, если в основании пирамиды четырёхугольник - четырёхугольной и т.д. Призма - многогранник, у которого две грани (основания) - одинаковы и взаимно параллельные многоугольники, а боковые грани – параллелограммы. Если рёбра призмы перпендикулярны плоскостям основания, призма называется прямой, если не перпендикулярны - наклонной. Правильные многогранники - имеют одинаковые грани в виде правильных многоугольников. Их особенностью является то, что каждый из них вписывается в сферу. Если все грани многогранника — правильные и равные треугольники, имеем дело с тетраэдром (правильный четырёхгранник); если все грани - правильные четырёхугольники (квадраты), имеем дело с гексаэдром или кубом (правильный шестигранник). Правильный восьмигранник — октаэдр; двенадцатигранник - додекаэдр и т.д. В общем виде поверхность вращения с важнейшими принадлежащими ей линиями имеет вид, изображённый на рис.11. Здесь же представлен и двухпроекционный комплексный чертёж её (определитель поверхности).
Изображения важнейших поверхностей вращения на двухпроекционном комплексном чертежепоказаны на рис. 12.
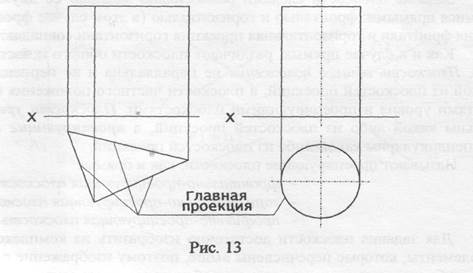
В заключение отметим, что из всех поверхностей вырожденную в своё основание проекцию (главную проекцию!) могут иметь только прямая призма и прямой цилиндр (см. рис. 13)
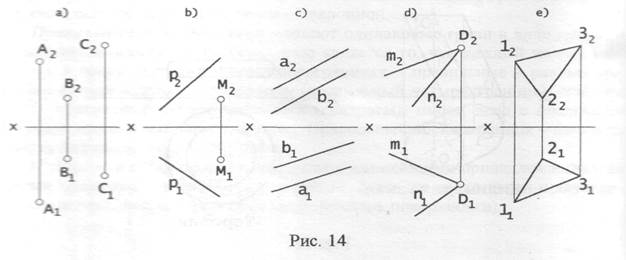
Плоскость Плоскость можно рассматривать как частный случай поверхности, когда и образующая и направляющая - прямые линии. Вообще же задать плоскость можно (рис. 14): - тремя точками, не лежащими на одной прямой (рис.14а) - прямой и не лежащей на ней точкой (рис. 14б); - двумя параллельными прямыми (рис. 14с); - двумя пересекающимися прямыми (рис.14д); - плоской фигурой (рис.14е); - следами плоскости.
След плоскости - прямая, по которой заданная плоскость пересекается с какой-либо плоскостью проекций.) От одного способа задания плоскости легко перейти к любому другому. Задание плоскости следами равносильно заданию её двумя пересекающимися прямыми: фронталью и горизонталью (в этом случае фронтальная проекция фронтали и горизонтальная проекция горизонтали совпадают с осью X). Как и в случае прямых, различают плоскости общего и частного положения. Плоскость общего положения не параллельна и не перпендикулярна одной из плоскостей проекций, а плоскости частного положения бывают плоскостями уровня и проецирующими плоскостями. Плоскости уровня - параллельны какой-либо из плоскостей проекций, а проецирующие плоскости перпендикулярны какой-либо из плоскостей проекций. Называют проецирующие плоскости, как и прямые: - фронтально-проецирующая плоскость; - горизонтально-проецирующая плоскость; - профильно-проецирующая плоскость.
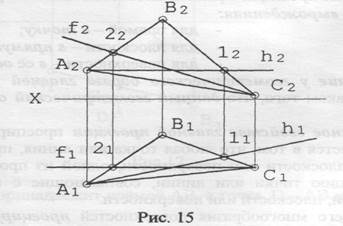
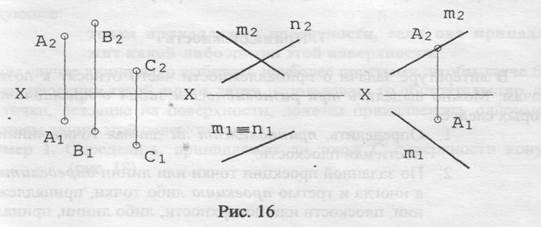
Заметим, что любая плоскость уровня - дважды проецирующая плоскость. Например, плоскость горизонтального уровня одновременно является плоскостью и фронтально-проецирующей, и профильно-проецирующей. Поэтому любая плоскость частного положения - плоскость проецирующая. Важнейшими линиями плоскостей являются их линии уровня. Горизонталями плоскости называют прямые, ей принадлежащие и параллельные горизонтальной плоскости проекций. Фронталями плоскости называют прямые, ей принадлежащие и параллельные фронтальной плоскости проекций. Для их построения необходимо использовать тот факт, что положение прямой определяется положением двух её точек. Если в качестве таких точек использовать обязательно принадлежащие плоскости точки, а также вспомнить, что фронтальная проекция горизонтали и горизонтальная проекция фронтали параллельна оси проекций X, эти прямые плоскости легко построить (рис. 15). Примеры проецирующих плоскостей приведены на рис.16.
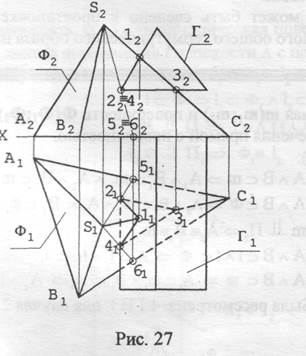
ОСНОВНЫЕ ВЫВОДЫ Принадлежность В литературе задачи о принадлежности часто относят к позиционным задачам. Можно выделить три разновидности задач о принадлежности, из которых следует: 1. Определить, принадлежит ли данная точка линии, поверхности или плоскости. 2. По заданной проекции точки или линии определить вторую, а иногда и третью проекцию либо точки, принадлежащей 3. Задать произвольную точку, принадлежащую заданной линии, поверхности, плоскости, либо задать произвольную линию, принадлежащую заданной поверхности или плоскости. Любая из разновидностей задач о принадлежности решается, в принципе, исходя из одних и тех же соображений. Рассмотрим подробнее возможные виды принадлежности и способы решения связанных с ними задач. А. Принадлежность точки линии. Основное положение в этом случае таково: точка принадлежит прямой, если ее проекции принадлежат одноименным проекциям этой прямой (рис. 17).
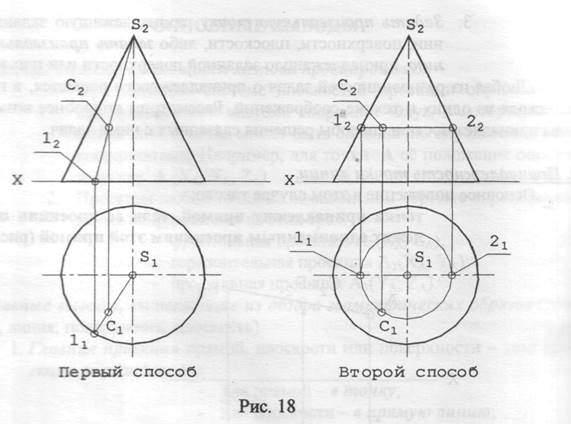
(На рис. 17 точка С принадлежит прямой АВ, а точка D - АВ не принадлежит). Б. Принадлежность точки поверхности. Основное положение при решении задач для этого варианта принадлежности следующее: точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности. В этом случае линии надо выбирать наиболее простыми, чтобы легче было построить проекции такой линии, затем использовать то обстоятельство, что проекции точки, лежащие на поверхности, должны принадлежать одноименным проекциям линии этой поверхности. Пример 1. Определить, принадлежит ли точка С поверхности конуса (рис. 18).
Здесь есть два пути решения, поскольку можно провести две простейших линии, принадлежащих конической поверхности. В первом случае — проводится прямая линия - образующая конической поверхности S1 так, чтобы она проходила через какую-либо заданную проекцию точки С. Тем самым предполагаем, что точка С принадлежит образующей S1 конической поверхности, а следовательно - самой конической поверхности. В этом случае одноименные проекции точки С должны лежать на соответствующих проекциях этой образующей. Другая простейшая линия - окружность с диаметром 1-2 (радиус этой окружности - отсчитывается от оси конуса до очерковой образующей). Этот факт известен еще из школьного курса геометрии: при пересечении кругового конуса плоскостью, параллельной его основанию, или перпендикулярной к его оси, в сечении будет получаться окружность. Второй способ решения позволяет найти недостающую проекцию точки С, заданной своей фронтальной проекцией, принадлежащей поверхности конуса и совпадающей на чертеже с осью вращения конуса, без построения третьей проекции. Всегда следует иметь в виду, видима или не видима точка, лежащая на поверхности конуса (в случае, если она не видна, соответствующая проекция точки будет заключена в скобки). Очевидно, что в нашей задаче точка С принадлежит поверхности, поскольку проекции точки принадлежат одноимённым проекциям линий, использованных для решения как при первом, так и при втором способе решения.
В. Принадлежность линии поверхности. Основное положение: линия принадлежит поверхности, если все тс линии принадлежат заданной поверхности.
Это означает, что в данном случае принадлежности должна быть несколько раз решена задача о принадлежности точки поверхности. Г. Принадлежность прямой плоскости Что касается принадлежности прямой плоскости, то здесь справедливы высказанные выше соображения относительно принадлежности к поверхности, с тем лишь условием, что для плоскости простейшей линией всегда является прямая, а положение прямой в пространстве однозначно определяется положением двух принадлежащих ей точек.
Пример 2. Задать произвольную точку К, принадлежащую плоскости, заданной двумя пересекающимися прямыми а и b (рис. 19). Решение. Можно взять какую-либо точку К, провести через нее прямую m, про которую точно можно сказать, что она принадлежит заданной плоскости, а потом определить вторую проекцию первоначально заданной произвольной точки. Можно сразу провести произвольную прямую плоскости, а затем определить положение произвольной точки плоскости, задав соответствующие проекции этой точки, принадлежащие проведенной прямой.
Главные позиционные задачи Как в геометрической, так и в конструкторской практике большое число решений относится к задачам о пересечении геометрических образов или геометрических тел. Ввиду их особой важности, задачи о пересечениях называют главными позиционными задачами (ГПЗ). Из всего разнообразия возможных при этом вариантов можно выделить две разновидности ГПЗ: - 1ГПЗ: пересечение линий и поверхностей; - 2ГПЗ: пересечение поверхностей. Очевидно, что сказанное о двух ГПЗ характеризует самый общий вариант для каждой из задач и подразумевает, что понятие каждого из компонентов пересечения (линия, поверхность) включает в себя все возможные его варианты. Так, к 1 ГПЗ относятся пересечения: - прямой линии и плоскости; - прямой линии и поверхности; - кривой линии и поверхности (в общем случае).
- плоскостей; - плоскости и поверхности; - поверхностей. Сущность всякой задачи на пересечение состоит в определении общего элемента, который будем называть искомым геометрическим образом. Очевидно, в 1-й ГПЗ это - точка или несколько (конечное число) точек (рис.22). Во 2-й ГПЗ искомым геометрическим образом является линия (рис.23). Искомый геометрический образ как результат пересечения заданных образов всегда принадлежит одновременно обоим заданным пересекающимся геометрическим образам и, очевидно, может быть определен: - непосредственно, исходя из свойств пересекающихся образов; - через посредство свойств нового геометрического образа
Направление методики решения предполагает использование проецирующих свойств геометрических образов. Поскольку геометрические образы могут быть как проецирующие, так и не проецирующие, очевидно, что как для 1 ГПЗ, так и для 2 ГПЗ при всем многообразии вариантов возможно существование трех случаев пересечения: Случай 1. Оба пересекающихся геометрических образа проецирующего характера; Случай 2. Один из пересекающихся геометрических образов проецирующего характера, а второй — не проецирующий; Случай 3. Оба пересекающихся геометрических образа - непроецирующего характера. Имея в виду то определение главной проекции геометрического образа, которое было дано ранее, очевидно, можно утверждать, что в случае 1 непосредственно на чертеже можно указать обе проекции искомого геометрического образа; в случае 2 непосредственно на чертеже можно определить одну проекцию искомого геометрического образа; В случае 3 определение проекций искомого геометрического образа потребует введения нового геометрического образа-посредника, обладающего свойствами проецирующих образов. Эти соображения вытекают из того, что точка, линия, фигура, принадлежащ ая проецирующему геометрическому образу, будет иметь свои одноименные проекции, совпадающие с главной проекцией этого образа. Все высказанное позволяет не только систематизировать все возможные случаи пересечения, но и алгоритмизировать сам процесс решения задач для все трех случаев. Самое главное из всего вышеизложенного о главных позиционных задачах (ГПЗ) можно объединить в двух таблицах, полезных для использования при решении задач о пересечении геометрических образов.
Чтобы увидеть общее в решении задач на пересечение и выяснить алгоритм для того или иного случая пересечения, рассмотрим решения ряда задач.
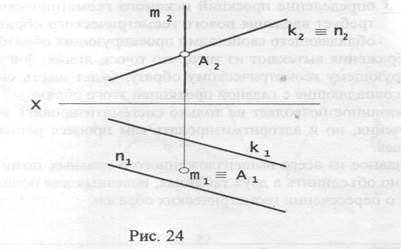
Задача 1. Даны прямая m(m1,m2) и плоскость Σ(n//k). Требуется определить точку А пересечения прямой m и плоскости Σ(n//k). Решение(рис.24): 1. А 2. А 1. m1 ╨ П1 => m1 ≡ A1 2. Σ ╨ П2 =>Σ2
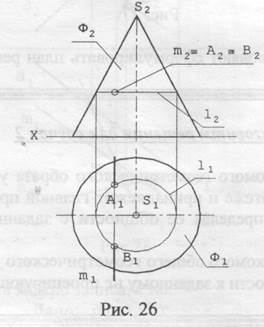
Задача 2. Заданы плоскость ˄ (˄2) и цилиндрическая поверхность Ф(Ф1, Ф2,) Определить линию пересечения l плоскости ˄ с поверхностью Ф. Решение (рис. 25): 1.l 2. l 3. ˄ ╨ П2 => l2 ≡ ˄2(l2 4. Ф ╨ П1 => Ф1 ≡ l1
Замечание. При рассмотрении интервала существования l необходимо помнить, что общность искомого геометрического образа определяет граница его существования в пределах общей принадлежности к заданным геометрическим образам (здесь эта граница определена точками 1 и 2).
Мы рассмотрели в задаче 1-1 ГПЗ, а в задаче 2-2 ГПЗ. Если сравнить их решения, можно заметить, что, во-первых, мы рассмотрели задачи, попадающие под первый случай пересечения, во-вторых, решение задач, в общем, не отличаются друг от друга. Значит, существует единый, общий для 1ГПЗ и для 2ГПЗ алгоритм решения, который мы сейчас и сформулируем.
Алгоритм решения для случая 1 1. Обе проекции искомого общего геометрического образа уже непосредственно заданы на чертеже. 2. Обе проекции искомого общего геометрического образа принадлежат главным проекциям проецирующих образов в пределах общности этих проекций. 3. Решение задачи может быть сведено к простановке обозначений проекций искомого общего геометрического образа на чертеже.
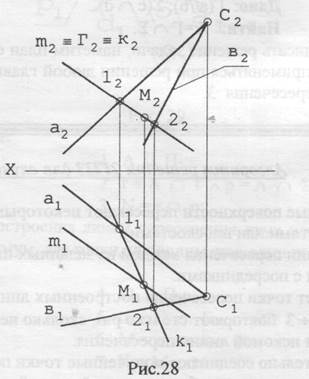
Примеры 3 и 4 позволяют сформулировать план решения задач для второго случая пересечения. Алгоритм решения для случая 2 1. Одна проекция искомого геометрического образа уже непосредственно задана на чертеже и принадлежит главной проекции проецирующего образа в пределах её общности с заданным не проецирующим образом. 2. Другая проекция искомого общего геометрического образа определяется по принадлежности к заданному не проецирующему образу. Задача 5.Заданы прямая m общего положения и плоскость общего положения Σ в виде двух пересекающихся прямых а и в. Определить точку М пересечения прямой m и плоскости Σ (рис. 28). Прежде, чем записать решение этой и следующей задачи, попробуем предложить следующий план решения. Алгоритм решения 1ГПЗ для случая 3 1. Через заданную прямую проводится плоскость-посредник; целесообразно, чтобы эта плоскость была проецирующего характера. 2. Строится линия пересечения заданной плоскости и плоскости-посредника (второй случай пересечения!). 3. Определяется точка пересечения заданной прямой и построенной линии пересечения, которая и будет искомой точкой. Эти же соображения можно сформулировать и в том случае, когда надо найти линию пересечения, а в качестве посредников выбраны некоторые поверхности. Сама же искомая линия будет представлена совокупностью точек.
Данные этой задачи можно записать так: Дано: m(m1, m2); Σ(a
Для задач на третий случай пересечения условимся записывать только решение в пространстве, что в более краткой форме отражает как суть производимых построений, так и применяемый алгоритм решения: 1. Г 2. k=Г 3. М = m Следует отметить, что посредник мог быть другим, однако в данном случае проецирующее свойство посредника позволило использовать алгоритм для второго случая пересечения, что упростило задачу. Рассмотрим еще один пример. Задача 6. Даны две плоскости общего положения: плоскость Г задана параллельными прямыми а иb, плоскость Σ - пересекающимися прямыми с и d. Найти линию k пересечения этих плоскостей. Кратко условие этой задачи можно записать так: Дано: Г(а//b); Σ(c Прежде чем записать решение задачи, наметим план её решения, который в дальнейшем будет применяться при решении любой главной позиционной задачи 2 для случая пересечения 3.
Алгоритм решения 2ГПЗ для случая 3 1. Обе заданные поверхности пересекают некоторыми посредниками 2. Строят линии пересечения каждой из заданных плоскостей или поверхностей с посредниками. 3. Определяют точки пересечения построенных линий пересечения. 4. Пункты 1-3 повторяют столько раз, сколько необходимо точек для 5. Последовательно соединяют полученные точки пересечения в некоторую линию, которая и будет искомой линией пересечения. В этом варианте решение может быть записано так (рис. 29):
Решение:
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.122.4 (0.29 с.) |
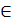 - принадлежит;
- принадлежит; - включает, содержит;
- включает, содержит;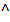 - и;
- и; ┴ - не перпендикулярно;
┴ - не перпендикулярно; ║- не параллельно;
║- не параллельно; - объединение;
- объединение; - пересекает;
- пересекает; ╨ - не проецирует (не проецирующий образ).
╨ - не проецирует (не проецирующий образ).