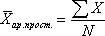Понятие статистического показателя. Формы выражения и виды статистических показателей

Статистический показатель - объективная количественная характеристика (мера) общественного явления или процесса 8 конкретных условиях места и времени. Каждый такой показатель имеет социально-экономическое содержание.

Формы выражения:

1) общее число единиц совокупности;

2) общая сумма значений количественного признака единиц совокупности;

3) средняя величина признака;

4) величина данного признака по отношению к величине другого.

Численное значение статистического показателя, выраженное в единицах измерения, называется его величиной.

Различают показатели экономического и социального развития общества: плановые (прогнозные) и отчетные (статистические). Плановые показатели определенные конкретные значения показателей, достижение которых прогнозируется в будущих периодах. Отчетные показатели - сложившиеся условия экономического и социального развития, достигнутый уровень за определенный период.

Статистические показатели условно подразделяют на первичные (объемные, количественные, экстенсивные) и вторичные (производные, качественные, интенсивные).

Первичные характеризуют общее число единиц совокупности либо сумму значений какого-то их признака.

Вторичные, производные показатели выражаются средними и относительными величинами.

Показатели, характеризующие размер сложного комплекса социально-экономических явлений и процессов, называют синтетическими.

В зависимости от применяемых единиц измерения различают показатели: натуральные, стоимостные и трудовые.

В зависимости от сферы применения различают показатели, исчисленные на региональном, отраслевом уровнях и т. д.

По точности отражаемого явления различают ожидаемые, предварительные и окончательные величины показателей.

По отношению к изучаемому свойству различают прямые и обратные показатели. Величина прямых показателей увеличивается с увеличением исследуемого явления, обратных показателей уменьшается с увеличением исследуемого явления.

В зависимости от объема и содержания объекта статистического изучения различают индивидуальные (характеризующие отдельные единицы совокуп­ности) и сводные (обобщающие) показатели.

Особенности обобщающих показателей: 1)дают сводную характеристику совокупностям

единиц изучаемых общественных явлений; 2) выражают существующие между явлениями связи, зависимости; характеризуют происходящие в явлениях изменения, складывающиеся закономерности их развития и т. д.

Аналитические показатели характеризуют статистическую совокупность. К ним относят:

1) средние величины;

2) показатели вариации;

3) показатели связи признаков;

4) показатели структуры и характера распределения;

5) показатели динамики;

6) показатели колеблемости;

7) показатели точности и надежности;

8) показатели точности и надежности прогнозов.

Система статистических показателей - совокупность статистических показателей, отражающих различные количественные аспекты и взаимосвязи изучаемых явлений и процессов.

Абсолютные величины.

Первичная статистическая информация выражается прежде всего в виде абсолютных показателей, которые являются количественной базой всех форм учета.

Абсолютные показатели характеризуют итоговую численность единиц совокупности или ее частей, размеры (объемы, уровни) изучаемых явлений и процессов, выражают временные характеристики. Абсолютные показатели могут быть только именованными числами, где единица измерения выражается в конкретных цифрах.

В зависимости от сущности исследуемого явления и поставленных задач единицы измерения могут быть натуральными (физические меры массы, длины, объема), условно-натуральными (например, молочные продукты с разным содержанием сливочной основы, мыло с разным содержанием жирных кислот и т.д.), стоимостными (денежное выражение) и трудовыми (затраты труда, трудоемкость технологических операций в человеко-днях, человеко-часах).

Вся совокупность абсолютных величин включает как индивидуальные показатели (характеризуют значения отдельных единиц совокупности), так и суммарные показатели (характеризуют итоговое значение нескольких единиц совокупности или итоговое значение существенного признака по той или иной части совокупности).

Абсолютные показатели следует также подразделить на моментные и интервальные.

Моментные абсолютные показатели характеризуют факт наличия явления или процесса, его размер (объем) на определенную дату времени.

Интервальные абсолютные показатели характеризуют итоговый объем явления за тот или иной период времени (например, выпуск продукции за квартал или за год и т. д.), допуская при этом последующее суммирование.

Относительные величины.

Относительные величины — это отвлеченные статистические величины, выражающие количественное соотношение двух величин. Относительные величины измеряются в коэффициентах, процентах, промилях, комплексных единицах.

Видыотносительныхвеличин:

1) относительные величины динамики-
это отношение фактической величины показателя в отчетном периоде (У₁) к фактической его величине в базисном, предшествующем периоде(У₀):

ОВД =(У₁ /У₀ )х100%.

Относительные величины динамики характеризуют изменение явления во времени. В статистике эти показатели называются темпами роста;

2) относительные величины выполнения плана-
это отношение фактической величины показателя (У₁) к плановой его величине (У_план) того же периода:

ОВВП =(У₁ /У_план)х 100%.

Эта относительная величина показывает степень выполнения плана в процентах;

3) относительная величина выполнения планового задания
это отношение планируемой величины показателя (У_план) к фактически достигнутой величине в предшествующем периоде, т.е. в базисном (у₀):

ОВПЗ=(У_план /У₀)х 100%.

Показывает, на сколько процентов плановое задание выше (ниже) фактически достигнутого в базисном периоде.Эту величину называют плановым темпом роста;

4) относительная величина структуры
— показы­вает состав явления, выраженный в форме доли или удельного веса. Доля (d) это отношение части к целому, т.е. отношение составныхчастей совокупности к ее общему объему. Удельный вес — это доля, выраженная в процентах. Относительные величины структуры используются в статистике для характеристики структурных сдвигов;
5) относительная величина координации - показывает соотношение частей целого, т.о. отношение последовательно всех частей к одной из них, взятой за базу. За базу принимаютнаименьшее значение. Относительная величина координации показывает, сколько единиц данной части целого приходится на другую ее часть, принятую за базу сравнения;
6) относительная величина интенсивности — это отношение двух разноименных величин, связанных между собой. Характеризует степень развития ка­кого либо явления в определенной среде;

7) относительная величина сравнения — это отношение одноименных величин, характеризующих разные объекты изучения за один и тот же период. Показывает, во сколько разчислитель больше (меньше) знаменателя.

 

27. Средняя арифметическая,способы ее расчета. Средняя гармоническая.

А) Средняя арифметическая - это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:

где X - значения величин, для которых необходимо рассчитать среднее значение; N - общее количество значений X (число единиц в изучаемой совокупности).

Средняя арифметическая взвешенная имеет следующий вид:

где f - количество величин с одинаковым значением X (частота).

Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X остутствует нижнияя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.

Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин.

Б) Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:

Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:

Например, автомобиль ехал из пункта А в пункт Б со скоростью 90 км/ч, а обратно - со скоростью 110 км/ч. Для определения средней скорости применим формулу средней гармонической простой, так как в примере дано расстояние w1=w2 (расстояние из пункта А в пункт Б такое, же как и из Б в А), которое равно произведению скорости (X) на время (f). Средняя скорость = (1+1)/(1/90+1/110) = 99 км/ч.

Средняя геометрическая и средняя хронологическая.

А) Средняя геометрическая применяется при определении средних относительных изменений.

Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.

 

28. Мода и медиана:понятие,принципы расчета и графического определния.
А) Статистическая мода - это наиболее часто повторяющееся значение величины X в статистической совокупности.
Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) или мультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.
Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:

где Мо – мода;

ХНМо – нижняя граница модального интервала;

hМо – размах модального интервала (разность между его верхней и нижней границей);

fМо – частота модальноого интервала;
fМо-1 – частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.

Б) Статистическая медиана – это значение величины X, которое делит упорядоченную по возрастанию или убыванию статистическую совокупность на 2 равных по численности части. В итоге у одной половины значение больше медианы, а у другой - меньше медианы.
Если X задан дискретно, то для определения медианы все значения нумеруются от 0 до N в порядке возрастания, тогда медиана при четном числе N будет лежать посередине между X c номерами 0,5N и (0,5N+1), а при нечетном числе N будет соответствовать значению X с номером 0,5(N+1).

Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:

где Ме – медиана;

ХНМе – нижняя граница медианного интервала;

hМе – размах медианного интервала (разность между его верхней и нижней границей);

fМе – частота медианного интервала;

fМе-1 – сумма частот интервалов, предшествующих медианному.
Также как и в случае с модой, при определении медианы если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.

29. Понятие вариации, ее значение.

Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности.
Термин «вариация» имеет латинское происхождение - variatio, что означает различие, изменение, колеблемость. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение.
Для измерения вариации признака используют как абсолютные, так и относительные показатели.

К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др.