
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляция и взаимосвязь величин. ⇐ ПредыдущаяСтр 6 из 6
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Коэффициент корреляции - это статистический показатель зависимости двух случайных величин. Коэффициент корреляции может принимать значения от -1 до +1. При этом, значение -1 будет говорить об отсутствии корреляции между величинами, 0 - о нулевой корреляции, а +1 - о полной корреляции величин. Т.е., че ближе значение коэффициента корреляции к +1, тем сильнее связь мезду двумя случайными величинами. Линейный коэффициент корреляции. Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона). Коэффициент корреляции рассчитывается по формуле:
Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. Коэффициент корреляции рангов (Кендалла). Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
Коэффициент корреляции рангов (Спирмена) Степень зависимости двух случайных величин (признаков) X и Y может характеризоваться на основе анализа получаемых результатов
Значение коэффициента меняется от −1 (последовательности рангов полностью противоположны) до +1 (последовательности рангов полностью совпадают). Нулевое значение показывает, что признаки независимы. Коэффициент множественной ранговой корреляции (конкордации).
Значимость:
В случае наличия связанных рангов:
Множественная корреляция. Множественная корреляция Измерении связи между результативным признаком, двумя и более факторными. Этим занимается множественная корреляция. Множественная корреляция решает три задачи. Она определяет: - форму связи; - тесноту связи; - влияние отдельных факторов на общий результат. Определение формы связи. Определение формы связи сводится обычно к отысканию уравнения связно с факторами x,z,w,...v. Так, линейное уравнение зависимости результативного признака от двух факторных определяется по формуле =a0+a1x+a2z Для определения параметров а0, a1и а2, по способу наименьших квадратов необходимо решить следующую систему трех нормальных уравнений: Измерение тесноты связи. При определении тесноты связи для множественной зависимости пользуются коэффициентом множественной (совокупной) корреляции, предварительно исчислив коэффициенты парной корреляции. Так, при изучении связи между результативным признаком y и двумя факторными признаками - х и z, нужно предварительно определить тесноту связи между у и х, между у и z, т.е. вычислить коэффициенты парной корреляции, а затем для определения тесноты связи результативного признака от двух факторных исчислить коэффициент множественной корреляции по следующей формуле: где rxy, rzy, rzx - парные коэффициенты корреляции. Коэффициент множественной корреляции колеблется в пределах от 0 до 1. Чем он ближе к 1, тем в большей мере учтены факторы, определяющие конечный результат.
Если коэффициент множественной корреляции возвести в квадрат, то получим совокупный коэффициент детерминации, который характеризует долю вариации результативного признака у под воздействием всех изучаемых факторных признаков. Совокупный коэффициент детерминации, как и при парной корреляции, можно исчислить по следующей формуле: R2=у2y/у2y где у2Y - дисперсия факторных признаков, у2y - дисперсия результативного признака. Однако вычисление теоретических значений Y при множественной корреляции и сложно, и громоздко. Поэтому факторную дисперсию у2Yисчисляют по следующей формуле: Проверка существенности связи при множественной корреляции по сути ничем не отличается от проверки при парной корреляции. Поскольку факторные признаки действуют не изолированно, а во взаимосвязи, то может возникнуть задача определения тесноты связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных коэффициентов корреляции. Например, при линейной связи частный коэффициент корреляции между х и у при постоянном z рассчитывается по следующей формуле: В настоящее время на практике широкое распространение получил многофакторный корреляционный анализ.
|
||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 733; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.178.207 (0.009 с.) |
 где
где 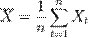 ,
,  — среднее значение выборок.
— среднее значение выборок. ,где
,где  .
. — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
— суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.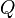 — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
— суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!) 

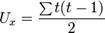

 — число связанных рангов в ряду X и Y соответственно.
— число связанных рангов в ряду X и Y соответственно. . Каждому показателю X и Y присваивается ранг. Ранги значений X расположены в естественном порядке i=1, 2,..., n. Ранг Y записывается как Ri и соответствует рангу той пары (X, Y), для которой ранг X равен i. На основе полученных рангов Х i и Yi рассчитываются их разности
. Каждому показателю X и Y присваивается ранг. Ранги значений X расположены в естественном порядке i=1, 2,..., n. Ранг Y записывается как Ri и соответствует рангу той пары (X, Y), для которой ранг X равен i. На основе полученных рангов Х i и Yi рассчитываются их разности  и вычисляется коэффициент корреляции Спирмена:
и вычисляется коэффициент корреляции Спирмена: 
 ,
, 
 — число групп, которые ранжируются.
— число групп, которые ранжируются. — число переменных.
— число переменных.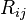 — ранг
— ранг  -фактора у
-фактора у  -единицы.
-единицы. ,
, 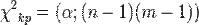 ,
,  , то гипотеза об отсутствии связи отвергается.
, то гипотеза об отсутствии связи отвергается.
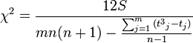 .
.


