
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка аналоговой и цифровой информации. Кодирование информации
Объект передачи и преобразования в вычислительных системах (машинах) – информация. В этом смысле вычислительную машину (систему) можно называть информационной, в отличие, например, от энергетической системы, где объект передачи и преобразования – энергия. Все процессы, происходящие в вычислительной системе, связаны непосредственно с различными физическими носителями информационных сообщений, и все узлы и блоки этой системы являются физической средой, в которой осуществляются информационные процессы. Специфика информационных процессов состоит не только в передаче информационных сообщений посредством заданной физической среды, но и в преобразовании, переработке и хранении информации. Информация определяет многие процессы в вычислительной машине. В самой общей форме процесс решения задачи на вычислительной машине проходит через следующие этапы: · ввод информации или установка исходных данных; · переработка или преобразование введенной информации; · определение результатов и вывод переработанной информации. Вычислительная машина получает информацию, запоминает ее, обрабатывает по заданным алгоритмам и направляет потребителю (пользователю) или в другие системы обработки. Ниже приводятся некоторые необходимые понятия. Аналоговый сигнал – сигнал, принимающий бесконечное число значений и заданный в непрерывном времени (определен для любого момента времени). Дискретный сигнал – сигнал, принимающий бесконечное число значений и заданный в дискретном времени (определен только в моменты времени, кратные периоду дискретизации Т). Цифровой сигнал – сигнал, принимающий конечное число значений, заданный в дискретном времени и представленный в виде цифровых кодов. Цифровой сигнал может быть получен из аналогового путем его дискретизации по времени (выполняется на основании теоремы отсчетов), квантования по уровню (выполняется с учетом динамического диапазона исходного аналогового сигнала) и кодирования. Под дискретизацией понимают переход от непрерывного сигнала к близкому (в определенном смысле) дискретному сигналу, описываемому разрывной функцией времени. Пример дискретного сигнала – последовательность коротких импульсов с изменяющейся амплитудой (последняя выступает в данном случае в качестве информативного параметра).
Обработка и передача дискретной информации имеет ряд преимуществ по сравнению с информацией, заданной в непрерывном виде. Дискретные сигналы в меньшей степени подвержены искажениям в процессе передачи и хранения, они легко преобразуются в двоичный цифровой код и обрабатываются с помощью цифровых вычислительных устройств. Процесс дискретизации состоит обычно из двух этапов: дискретизации по времени и дискретизации (квантования) по уровню. Дискретизация аналогового сигнала по времени – процесс формирования выборки аналогового сигнала в моменты времени, кратные периоду дискретизирующей последовательности Dt. Дискретизирующая последовательность – периодическая последовательность отсчетов времени, задающая сетку дискретного времени. Период дискретизации Dt – интервал времени между двумя последовательными отсчетами аналогового сигнала (шаг дискретизации по времени). При выборе частоты дискретизации по времени можно воспользоваться теоремой В.А. Котельникова. Теорема отсчетов (теорема Котельникова) – теорема, определяющая выбор периода дискретизации Дt аналогового сигнала в соответствии с его спектральной характеристикой. Согласно теореме, всякий непрерывный сигнал, имеющий ограниченный частотный спектр, полностью определяется своими дискретными значениями в моменты отсчета, отстоящие друг от друга на интервалы времени Dt = l/(2Fmax), где Fmax – максимальная частота в спектре сигнала. Иначе, дискретизация по времени не связана с потерей информации, если частота дискретизации fдискр = 1/Dt в два раза выше указанной верхней частоты сигнала Fmax. Согласно теореме Котельникова, нет необходимости передавать бесконечное множество всех значений непрерывного сигнала x(t), достаточно передавать лишь те его значения (рис. 3.4), которые отстоят друг от друга на расстоянии Dt = l/(2Fmax). Для восстановления сигнала x(t) на вход идеального фильтра низких частот, имеющего полосу пропускания частот от 0 до Fmax, необходимо подать последовательность узких импульсов с амплитудой, соответствующей дискретным отсчетам сигнала x(ti) в моменты времени ti=iDt.
Поскольку теорема отсчетов (теорема Котельникова) сформулирована для сигнала с ограниченным спектром, а реальные сигналы имеют неограниченную спектральную плотность, то при расчетах Dt=1/(2Fmax) используют приближенное значение Fmax (например, активную ширину спектра, определенную по амплитудному критерию, по критерию 90%-ного содержания энергии или средней мощности сигнала). Кроме того, и идеальный фильтр низких частот, необходимый для восстановления сигнала в соответствии с теоремой, является физически нереализуемым, так как предъявляемые к нему требования (идеально прямоугольная форма амплитудно-частотной характеристики, отсутствие фазового сдвига в рассматриваемой полосе частот от 0 до Fmax) оказываются противоречивыми и могут выполняться лишь с определенной погрешностью. Учитывая сказанное, частоту дискретизации по времени обычно принимают в 1,5–2,5 раза больше значения, рассчитанного по теореме Котельникова, т.е. fдискр = (3 – 5)Fmax. Существуют и другие способы выбора частоты дискретизации сигнала (с учетом времени корреляции передаваемого сообщения, значения наибольшего или среднеквадратичного отклонения процесса и т. д.). Так, в соответствии с критерием Н.А.Железнова, который выполняется для случайных сигналов, имеющих конечную длительность Тс и неограниченный частотный спектр, рекомендуется принимать шаг дискретизации Дt, равный максимальному интервалу корреляции сигнала ф0. Предполагается, что параметр ф0, характеризует такой промежуток времени, в пределах которого отдельные значения случайного процесса можно считать статистически зависимыми (коррелированными), причем ф0“Тс. Таким образом, исходный непрерывный сигнал заменяется совокупностью N = Тс/ф0 некоррелированных отсчетов (импульсов), следующих с частотой fдискр=1/Dt=1/ф0. При этом восстановление сигнала x(t) осуществляется с помощью линейного прогнозирующего фильтра со среднеквадратической ошибкой, сколь угодно мало отличающейся от нуля в промежутке времени, равном интервалу корреляции ф0. Более полно учитывая свойства реальных сигналов (конечная длительность, неограниченность спектра), критерий Железнова тем не менее исходит из допущения о равенстве нулю корреляционной функции сигнала Kx(ф) вне интервала [–ф0; ф0], что на практике выполняется с определенной погрешностью. В тех случаях, когда имеется более подробная информация о законе изменения сигнала, выбор частоты дискретизации можно осуществлять исходя из допустимой погрешности аппроксимации функции x(t) на каждом из интервалов дискретизации. На рис. 3.5 дан пример кусочно-линейной аппроксимации, когда соседние отсчеты функции x(t), взятые в дискретные моменты времени ti, и ti+1, соединяются отрезками прямых.
Рассмотренные способы равномерной дискретизации (при Dt = const) иногда могут приводить к получению избыточных отсчетов, не оказывающих существенного влияния на процесс восстановления исходного сообщения. Например, если функция x(t) мало изменяется на некотором, достаточно протяженном интервале времени Т0, то соответствующие дискретные отсчеты сигнала практически не отличаются друг от друга и, следовательно, нет необходимости использовать все указанные отсчеты для хранения или передачи информации по линии связи. Сокращение избыточной информации возможно на основе способов адаптивной (неравномерной) дискретизации, обеспечивающих выбор интервала Dt между соседними отсчетами с учетом фактического изменения характеристик сигнала (в частности, скорости его изменения).
Квантование (дискретизация) сигнала по уровню – процесс отображения бесконечного множества значений аналогового сигнала на некоторое конечное множество (определяемое числом уровней квантования). Отличительной особенностью дискретизации по уровню является замена непрерывной шкалы уровней сигнала x(t) дискретной шкалой xD.i(I = 1, 2,...,m), в которой различные значения сигнала отличаются между собой не менее чем на некоторое фиксированное (или выбираемое в процессе квантования) значение Дx, называемое шагом квантования. Шаг квантования – величина, равная интервалу между двумя соседними уровнями квантования (определена только для случая равномерного квантования). Необходимость квантования вызвана тем, что цифровые вычислительные устройства могут оперировать только с числами, имеющими конечное число разрядов. Таким образом, квантование представляет собой округление передаваемых значений с заданной точностью. При равномерном квантовании (Dx=const) число разрешенных дискретных уровней xi составляет:
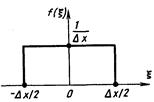
где xmax и xmin – соответственно верхняя и нижняя границы диапазона изменения сигнала. Ошибка квантования – величина, определяемая как x(х) = x – xD.i, где x – кодируемая дискретная величина, xD.i – дискретизированный сигнал. Шум квантования – случайная функция времени, определяемая как зависимость ошибки квантования от времени. Чем меньше значение Dx, тем меньше получаемая ошибка. Если в результате квантования любое из значений сигнала х(t), попавшее в интервал (хD.i – Dх/2; хD.i + Dх/2), округляется до хD, то возникающая при этом ошибка x(х) не превышает половины шага квантования, т.е. max|x (х)|=0,5Dx. На практике шаг квантования Dx выбирают исходя из уровня помех, в той или иной форме присутствующих при измерении, передаче и обработке реальных сигналов. Если функция x(t) заранее неизвестна, а шаг квантования Dх достаточно мал по сравнению с диапазоном изменения сигнала (xmax–xmin), то принято считать ошибку квантования x(х) случайной величиной, подчиняющейся равномерному закону распределения. Тогда, как показано на рис. 3.6, плотность вероятности f1(x) для случайной величины x, принимает значение 1/(Dх) внутри интервала (–Dх/2; +Dх/2) и равна нулю вне этого интервала. В данном случае дисперсию D[x] ошибки квантования x, находят как
Рис. 3.6. Равномерный закон распределения ошибки квантования При Dх=const относительная погрешность квантования Dx = x (х)/x существенно зависит от текущего значения сигнала x(t). В связи с этим при необходимости обработки и передачи сигналов, изменяющихся в широком диапазоне, нередко используется неравномерное (нелинейное) квантование, когда шаг Dх принимается малым для сигналов низкого уровня и увеличивается с ростом соответствующих значений сигнала (например, Dх выбирают пропорционально логарифму значения |x(t)|). Выбор шага Dхi=xD.i–xD.i-1 осуществляется еще и с учетом плотности распределения случайного сигнала (для более вероятных значений сигнала шаг квантования выбирают меньшим, для менее вероятных – большим). Таким образом удается обеспечить высокую точность преобразования при ограниченном (не слишком большом) числе разрешенных дискретных уровней сигнала x(t). Процесс преобразования дискретного сигнала в цифровой называют кодированием информации, а множество различных кодовых комбинаций, получаемых при данном правиле кодирования, – кодом. Важной характеристикой кода является основание (или значность) кода m, т. е. число возможных значений, которые могут принимать элементы кодовой комбинации. Пусть требуется передать сигнал, уровень которого изменяется от 0 до 10 В. Если шаг квантования данных составляет 10 мВ, то каждый отсчет сигнала можно рассматривать как одно из 1000 возможных сообщений. Для передачи этой информации можно предложить различные способы: а) каждому сообщению поставить в соответствие определенный уровень напряжения, при этом основание кода m=1000, а длина кодовой комбинации (слова) принимает минимальное значение n=1; б) можно воспользоваться двоичным (бинарным) представлением амплитуды сигнала с m=2, но тогда потребуется комбинация длины n=10 (210=1024, так что некоторые комбинации здесь не использованы). Примером двоичного кода является запись натурального числа А в позиционной двоичной системе счисления, осуществляемая по следующему правилу:
Здесь символы а1, а2, …, an принимают значения 0 или 1, n – число разрядов в коде. Предполагается, что символ a1, расположенный в старшем разряде кодовой комбинации, имеет наибольший вес 2n-1, тогда как вес символа an в младшем разряде является минимальным и равен 20=1. Для представления дробных чисел, значения которых не превышают единицы, обычно используют запись в следующем виде:
т. е. веса разрядов кодовой комбинации а1, а2, …, an здесь равны 2-1, 2-2,..., 2-n. В тех случаях, когда число А может принимать очень большие или же очень малые значения, удобнее использовать представление числа в форме с плавающей запятой. При этом каждое десятичное число определяется мантиссой, принимающей дробные значения от 0,1 до 1, и порядком – показателем степени числа 10. Например, число 50 представляется как 0,5·102, а число 0,00105 записывается в виде 0,105·10-2. Соответственно представление в двоичном коде для числа А должно производиться отдельно – для мантиссы и для порядка числа А.
Возможны и промежуточные варианты. Поэтому целесообразно поставить вопрос об определении оптимальной пары значений m и n. В качестве критерия оптимальности S примем минимум произведения числа требуемых символов (уровней) m на длину кодовой комбинации n, необходимой для представления заданного числа сообщений N. Тогда можно записать S=min(mn)=min(m log2 N/ log2 m)
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.246.203 (0.024 с.) |





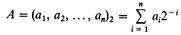 ,
,


