
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 13. Угловая модуляция
1. Фазовая модуляция. 2. Частотная модуляция. 3. Спектр ФМ и ЧМ колебании. 4. Схемная реализация частотной модуляции. 5. Схемная реализация фазовой модуляции.
Фазовая модуляция Два вида угловой модуляции: фазовая и частотная. Фазовая модуляция (ФМ) заключается в изменении фазы j переносчика
где а - коэффициент пропорциональности. Амплитуда колебания при ФМ не изменяется, поэтому аналитическое выражение ФМ колебания имеет вид
Если модуляция осуществляется гармоническим сигналом
Первые два слагаемых в выражении (3) определяют фазу немодулированного колебания, третье - изменение фазы колебания в результате модуляции. ФМ -колебание характеризуется векторной диаграммой рис.1, построенной на плоскости, вращающейся по часовой стрелке с угловой частотой wо. Немодулированному колебанию соответствует неподвижный вектор Uo. Фазовая модуляция заключается в периодическом с частотой W повороте вектора U относительно Uo на угол Крайние положения вектора U обозначены U' и U ". Максимальное отклонение фазы модулированного колебания от фазы немодулированного колебания
называется индексом модуляции. Индекс модуляции М пропорционален амплитуде Х модулирующего сигнала. Выражение для ФМ колебания можно переписать в виде
Мгновенная частота ФМ колебания
Таким образом, ФМ колебание в разные моменты времени имеет различные мгновенные частоты, отличающиеся от частоты несущего колебания wо на величину Наибольшее отклонение частоты w от несущей частоты wо называется девиацией частоты Dwд = М W
Частотная модуляция Частотная модуляция заключается в изменении мгновенной частоты переносчика пропорционально первичному сигналу:
Мгновенная фаза ЧМ колебания равна
Аналитическое выражение ЧМ колебания с учетом постоянства амплитуды можно записать в виде
В простейшем случае модуляции гармоническим колебанием Аналитическое выражение для ЧМ сигнала
Индекс модуляции М =Dwд/W. Тогда ЧМ колебание можно записать в виде
Из сказанного следует, что ФМ и ЧМ колебания имеют много общего. Так, колебание вида (10) может быть результатом как ФМ, так и ЧМ гармоническим первичным сигналом. Кроме того, ФМ и ЧМ характеризуются одними и теми же параметрами (индексом модуляции М и девиацией частоты Dwд). Наряду с отмеченным сходством ЧМ и ФМ между ними имеется и существенно отличие, связанное с различным характером зависимости величин М и DwД от частоты W первичного сигнала: - при ФМ индекс модуляции не зависит от частоты W, а девиация частоты пропорциональна W; - при ЧМ девиация частоты не зависит от частоты W, а индекс модуляции обратно пропорционален W. В общем случае любое колебаний с угловой модуляцией может быть получено как в результате ФМ первичным сигналом x(t), так и ЧМ первичным сигналом x1 (t)= Средняя мощность ЧМ (ФМ) колебания. Так как обычно W << w, то можно считать рассматриваемые колебания в пределах периода T =2p/w гармоническими. Средняя мощность такого колебания за период T
Такой же она будет и в другие периоды, а поэтому и за период низкой частоты. Следовательно, средняя мощность при ЧМ и ФМ остается такой же, как и в отсутствие модуляции; происходит лишь ее перераспределение между составляющими спектра.
Спектр ФМ и ЧМ колебаний При узкополосной модуляции M < 1, спектр ЧМ (ФМ) колебаний аналогичен спектру простейшего АМ колебания. Он содержит компоненты несущей частоты wо и двух боковых частот wо+W и wо-W:
Параметром, определяющим амплитуды боковых частот, здесь является индекс модуляции M. Ширина спектра узкополосной угловой модуляции такая же, как и при АМ: она равна удвоенной частоте модуляции. Несмотря на идентичность спектров, рассматриваемое колебание отличается от АМ колебания, что является следствием различия в знаках (т.е. сдвиге фаз на 180о) компонент нижней боковой частоты. Это иллюстрирует векторная диаграмма рис.3.
При широкополосной угловой модуляции M >> 1. В этом случае выражение для спектра имеет достаточно сложный вид. На рис.5 в качестве примера приведен спектр ФМ (ЧМ) сигнала при модуляции гармоническим сигналом. Практическая ширина спектра близка к удвоенной девиации частоты DwЧМ,ФМ» 2Dwд = 2 M W. (13) При модуляции гармоническим сигналом спектр ЧМ и ФМ колебаний оказывается дискретным, симметричным относительно wо и содержащим бесконечное число боковых частот вида wо± n W с амплитудами An = UoJn(M) (Jn(M) -функции Бесселя n -го порядка). В качестве примера на рис.4 приведен спектр для M =4. Соотношения между функциями Бесселя различных порядков, а следовательно, и между амплитудами различных боковых компонент определяются индексом модуляции M. При некоторых значениях M отдельные компоненты могут исчезнуть (Jn(M) =0). Это же относится к амплитуде несущей частоты, которая обращается в ноль при M =2.4; 5.6¼ Наличие бесконечно большого числа боковых компонент спектра означает, что теоретически спектр ФМ и ЧМ колебания является бесконечно широким. Однако функции Бесселя, начиная с некоторых n < M, быстро убывают с ростом n. Это позволяет ограничить полезный (практический) спектр таких сигналов определенным количеством боковых частот. При ограничении спектра необходимо учитывать влияние двух противоречивых факторов: в более узкой полосе частот ослабляется влияние помех, но одновременно увеличиваются искажения сигнала из-за отсутствия опускаемых составляющих. На практике выбирают компромиссное решение. Если ограничиться в спектре боковыми составляющими, амплитуда которых не превосходит q % от максимальной амплитуды спектральной компоненты Ux, то для каждого M можно рассчитать соответствующую ширину спектра. Она окажется несколько большей 2 М W = 2Dwд. Из рис.4 следует, что для M =4 при q =20% ширина спектра DwЧМ,ФМ= 2(M +3)W = 2(Dwд+3W). При больших индексах модуляции (порядка десятков и сотен), практическая ширина спектра, подсчитанная подобным образом, близка к удвоенной девиации частоты. При изменении амплитуды Х модулирующего сигнала спектры ФМ и ЧМ колебаний изменяются одинаково. При возрастании Х происходит пропорциональное увеличение индекса модуляции, спектры расширяются за счет увеличения числа спектральных компонент. Изменение частоты W модулирующего колебания по-разному влияет на изменение спектров ФМ и ЧМ колебаний. При ФМ изменение частоты W не влияет на величину индекса модуляции, а следовательно, и на число спектральных составляющих (рис.5). При ЧМ с уменьшением W индекс модуляции увеличивается, что приводит к увеличению числа спектральных компонент (рис.5). В итоге ширина спектра ЧМ колебания от частоты почти не зависит, а при ФМ изменяется пропорционально W. На практике часто используется фазовая манипуляция, при которой фаза несущей изменяется на 180о. Графики изменения фазы Dj(t) и фазоманипулированного сигнала показаны на рис.6. Амплитудный спектр такого сигнала приведен на рис.7. Он содержит только боковые частоты вида wо± n W (с нечетными n).
13.4Схемная реализация частотной модуляции Для получения частотной модуляции нужно, чтобы частота колебаний автогенератора изменялась под действием первичного сигнала u W. На рис.8 приведена схема автогенератора (обведена пунктирной линией), вырабатывающей синусоидальное напряжение
Рассмотрим случай, когда в качестве сопротивления Xу используется емкость С' = C1 + D C(t). Частота генерируемых колебаний определяется формулой
где Cо = С + C1; Изменение общей емкости контура на величину D C вызывает изменение частоты на Dw = w - wо. Разлагая правую часть (14) в ряд Тейлора и ограничивая для D C/Cо << 1 первыми двумя членами разложения, получаем Dw/wо = -D C/(2Cо). (15) Если изменить индуктивность контура L = Lo + D L(t) так, чтобы D L/Lо << 1, относительное изменение частоты будет Dw/wо = -D L/(2Lо). (16)
В рассмотренных случаях изменение частоты колебаний происходит пропорционально изменениям D C(t) и D L(t). Знак "-" в (15) и (16) является следствием того, что увеличение индуктивности или емкости контура ведет к уменьшению частоты колебаний. Из выражений (15) и (16) следует, что если D C(t) и D L(t) изменяются пропорционально первичному сигналу и притом в небольших пределах, изменение частоты также пропорционально u W, т.е. частотная модуляция будет неискаженной. В качестве управляемого сопротивления в транзисторных генераторах обычно используют варикапы. На рис.9 показана схема автогенератора с подключенным в контур варикапом. От источника постоянного напряжения на варикапе VD обеспечивается постоянное обратное напряжение смещения Ем, определяющее начальную емкость варикапа Со. На варикап относительно выбранной рабочей точки подается управляющее напряжение u W, пропорциональное модулирующей функции. Изменение управляющего напряжения приводит к изменению емкости варикапа и, следовательно, частоты генерируемых колебаний. Остальные элементы схемы имеют вспомогательное значение: емкость Ср большой величины разделяет цепи питания генератора и варикапа по постоянному току, позволяя в каждой из них установить нужные напряжения; добавочное сопротивление Rд (величиной порядка сотен килоом) включается для того, чтобы источник смещения и вторичная обмотка трансформатора не шунтировали контур генератора.
Вольт - парадная характеристика варикапа показана на рис.10.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.28.197 (0.019 с.) |
 пропорционально первичному сигналу x(t):
пропорционально первичному сигналу x(t): , (1)
, (1)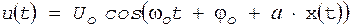 . (2)
. (2)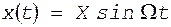 , то мгновенная фаза
, то мгновенная фаза . (3)
. (3) .
.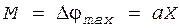 (4)
(4) . (5)
. (5) . (6)
. (6) , что позволяет рассматривать ФМ колебание как модулированное по частоте.
, что позволяет рассматривать ФМ колебание как модулированное по частоте. . (7)
. (7)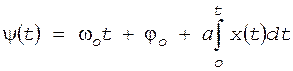 . (8)
. (8) . (9)
. (9) мгновенная частота колебания равна
мгновенная частота колебания равна  , где
, где  - девиация частоты, т.е. максимальное отклонение частоты от несущей wО, вызванное модуляцией.
- девиация частоты, т.е. максимальное отклонение частоты от несущей wО, вызванное модуляцией. . (10)
. (10)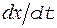 (т.к. фаза колебания представляет собой интеграл от частоты). Следует также отметить, что частотная и фазовая модуляции различаются также способами их осуществления.
(т.к. фаза колебания представляет собой интеграл от частоты). Следует также отметить, что частотная и фазовая модуляции различаются также способами их осуществления. . (12)
. (12)
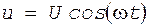 с частотой w приблизительно равной резонансной частоте контура wо. Следовательно, изменение частоты генерируемых колебаний может быть достигнуто изменением емкости или индуктивности контура. Для осуществления частотной модуляции параллельно контуру генератора подключают параметрический элемент - реактивное управляемое сопротивление Xу(t), величина которого изменяется под действием модулирующего сигнала.
с частотой w приблизительно равной резонансной частоте контура wо. Следовательно, изменение частоты генерируемых колебаний может быть достигнуто изменением емкости или индуктивности контура. Для осуществления частотной модуляции параллельно контуру генератора подключают параметрический элемент - реактивное управляемое сопротивление Xу(t), величина которого изменяется под действием модулирующего сигнала.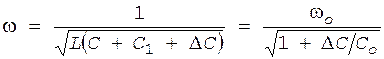 , (14)
, (14) .
.


