
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тождества логики высказываний, правильные рассуждения.Стр 1 из 2Следующая ⇒
Тождества логики высказываний, правильные рассуждения. Формула называется тавтологией (или тождественно-истинной), если на любых оценках своего списка переменных она принимает значение 1. В последнем столбце таблицы истинности этой формулы 0 нет. Формула называется выполнимой, если на некоторой оценке своего списка переменных она принимает значение 1. В последнем столбце таблицы истинности этой формулы есть хоть одна 1. Формула называется тождественно-ложной, если на любых оценках своего списка переменных она принимает значение 0. В последнем столбце таблицы истинности этой формулы 1 нет. Формула называется опровержимой, если на некоторой оценке своего списка переменных она принимает значение 0. В последнем столбце таблицы истинности этой формулы есть хоть один 0. Рассуждение называется правильным, если из конъюнкции посылок следует заключение, т.е. всякий раз, когда все посылки истинны, заключение тоже истинно.
Двойственность. Закон двойственности. Логические символы
Разрешимость для логики высказываний. Контактные схемы. Разрешимость для логики высказываний – это существует ли процедура, позволяющая для каждой формулы за конечное число шагов определить, является ли эта формула тавтологией. Логика высказываний разрешима, так как для каждой формулы можно построить её таблицу истинности. Существует и другая процедура проверки того, что формула является тавтологией: формула является тавтологией тогда и только тогда, когда для каждой её КНФ в любую из элементарных дизъюнкций (скобок) входят одновременно какая-то переменная и её отрицание.
Нормальные формы формул. Теорема о единственности СДНФ и СКНФ. Формула находится в дизъюнктивной нормальной форме (ДНФ), если она является дизъюнкцией (может быть и одночленной) элементарных конъюнкций. Например, формулы (x Из всех нормальных форм формулы выделим совершенные формы. Из ДНФ выделим Совершенную ДНФ (СДНФ). Формула находится в СДНФ относительно своего списка переменных, если каждый её дизъюнктивный член содержит по одному разу в прямом или инверсном виде все переменные формулы, и все её дизъюнктивные члены попарно различны. Например, формула в СДНФ: (x & y & z) Теорема Поста, её необходимость. Таблица Поста. Теорема Поста: для того, чтобы система булевых функций F = {F1, …, Fm} была полной, необходимо и достаточно, чтобы для каждого из классов T Доказательство необходимости: Классы T
Аксиоматические теории. Определения и свойства исчисления высказываний. Исчисление высказываний – это пример аксиоматической теории. ИВ определяется следующим образом: 1. Алфавит ИВ – это высказывательные переменные, скобки: (,) и логические символы
2. Имеется подмножество выражений, называемое формулами ИВ. Формулы ИВ: а) все высказывательные переменные – это формулы; б) если A и B формулы, то 3. Выделено некоторое подмножество формул, называемое аксиомами ИВ. Каковы бы не были формулы A, B и C, следующие формулы являются аксиомами ИВ: A1. A A2. (A A3. ( Выражения A1 – A3 называются схемами аксиом, поскольку каждое из них порождает бесконечное множество аксиом ИВ. Например, формула X 4. Имеется правило вывода ИВ, позволяющее из предыдущих формул вывода получать последующие. Выводом в ИВ называется всякая последовательность формул ИВ (шагов вывода) такая, что любая формула есть либо аксиома или теорема ИВ, либо получена из предыдущих формул вывода с помощью правила вывода ИВ. Формула T называется теоремой ИВ, если существует вывод, в которой эта формула является последней. Этот вывод называется выводом теоремы T ИВ: Правило вывода m.p.(modus ponens): если в выводе есть две формулы вида А Все аксиомы ИВ – это тавтологии, что можно проверить по их таблице истинности. По правилу m.p. из тавтологий можно получить только тавтологии. Тождества логики высказываний, правильные рассуждения. Формула называется тавтологией (или тождественно-истинной), если на любых оценках своего списка переменных она принимает значение 1. В последнем столбце таблицы истинности этой формулы 0 нет. Формула называется выполнимой, если на некоторой оценке своего списка переменных она принимает значение 1. В последнем столбце таблицы истинности этой формулы есть хоть одна 1. Формула называется тождественно-ложной, если на любых оценках своего списка переменных она принимает значение 0. В последнем столбце таблицы истинности этой формулы 1 нет. Формула называется опровержимой, если на некоторой оценке своего списка переменных она принимает значение 0. В последнем столбце таблицы истинности этой формулы есть хоть один 0. Рассуждение называется правильным, если из конъюнкции посылок следует заключение, т.е. всякий раз, когда все посылки истинны, заключение тоже истинно.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.107.241 (0.017 с.) |
 и
и  называют двойственными друг другу. Формула А
называют двойственными друг другу. Формула А 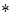 двойственна формуле А, если она получена из А одновременной заменой
двойственна формуле А, если она получена из А одновременной заменой  C) двойственна формуле F
C) двойственна формуле F  B, то A
B, то A  x
x  y
y  , T
, T  , S, L и M нашлась функция Fj из системы F, не принадлежащая этому классу.
, S, L и M нашлась функция Fj из системы F, не принадлежащая этому классу. . Любой набор символов алфавита ИВ (даже бессмысленный) – это выражение ИВ.
. Любой набор символов алфавита ИВ (даже бессмысленный) – это выражение ИВ. T. Слева от символа
T. Слева от символа  В и А, то после них в выводе можно писать формулу В. Считается, что формула В получена по правилу m.p. из формул А и А
В и А, то после них в выводе можно писать формулу В. Считается, что формула В получена по правилу m.p. из формул А и А  или А, А
или А, А 


