
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6. Показатели вариации.
Вариация признаков и причины ее порождающие. Показатели вариации и их значение в статистике. Дисперсия, ее свойства и методы расчета. Теория сложения дисперсий. Вопрос 1. Различия индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов, которые по разному сочетаются в каждом отдельном случае. Средняя величина является обобщающей характеристикой признака изучаемой совокупности, но она не показывает строение совокупности. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее. Если отдельные варианты недалеко отстоят от средней, то мы говорим, что данная средняя хорошо представляет изучаемую совокупность. Для того чтобы изучить, как велики эти отклонения, их измеряют при помощи показателей вариации.
Вопрос 2. Ряд распределения, образующийся в результате накопления статистической информации по значению варьирующего признака, является наиболее фундаментальной характеристикой совокупности. Он дает наиболее полное представление о результатах действия и взаимодействия всех факторов явления (основных и случайных) о сложившейся под их влиянием закономерностей ряда распределения, о свойствах индивидуальных значений признака и их особенностях. Изучение ряда распределения позволяет установить связь единичного и массового, частного и общего, случайного и закономерного. Для более глубокого изучения ряда распределения варьирующего признака служат следующие показатели вариации: 1. Размах вариации, которых представляет собой разность между максимальным и минимальным значением признака, т.е. амплитуду колебания вариации в ряду распределения.
2. Среднее линейное отклонение представляет собой среднюю величину из абсолютных отклонений вариант признака от средней и рассчитывается по формуле: невзвешенное
взвешенное Среднее линейное отклонение выражается в тех же единицах измерения, что и сам признак. Среднее линейное отклонение дает приблизительную оценку вариации признака в рядах распределения, т.к. не учитывает колебаний признака в ряду. Для более точной оценки вариации признака в ряду распределения служит дисперсия или средний квадрат отклонения.
3. Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины. Рассчитывается по формуле: s простая взвешенная Взвешенная дисперсия служит для расчета среднего квадратического отклонения. 4. Среднее квадратическое отклонение определяется по формуле: простое взвешенное Среднее квадратическое отклонение показывает отклонение различных индивидуальных значений признака в ряду распределения от среднего уровня. Измеряется в тех же единицах, что и сам признак. Среднее квадратическое отклонение является более точной характеристикой вариации признака в ряду распределения по сравнению со средне линейным отклонением, т.к. учитывает внутренние колебания признака в ряду распределения. Для интервального вариационного ряда распределения среднее квадратическое отклонение определяется по формуле:
где i – величина интервала; m1 - момент первого порядка m2 - момент второго порядка 5. Коэффициент вариации признака в совокупности представляет собой относительную колеблемость признака в совокупности, и рассчитывается по формуле: - по среднелинейному отклонению - по среднеквадратическому отклонению Коэффициент вариации показывает на сколько % отклоняется индивидуальное значение признака в ряду распределения от среднего уровня. Допустимые пределы колебания признака в ряду приблизительно 30-35%, тогда совокупность признается однородной. Если эти пределы превышаются то данная совокупность должна быть подвергнута преобразованию с целью приведения к нормальному распределению.
Каждый ряд распределения графически может быть представлен кривой распределения. Идеальной формой распределения является нормальное, которое изображается с помощью теоретической кривой распределения или кривой Лапласа-Гауса.(эта кривая отражает общую закономерность данного типа распределения). Кривая распределения фактических данных является полигоном распределения. Большинство фактических распределений близки к нормальному и отличаются от него нарушением симметрии или расположения вершины кривой. Причина таких смещений - ошибки наблюдения и сбора данных. Для характеристики смещений фактического ряда распределения использую показатели асимметрии и эксцесса.
1. Коэффициент асимметрии определяется по формуле: где m3 - момент третьего порядка s3 - куб среднего квадратического отклонения. Коэффициент асимметрии для теоретических кривых нормального распределения равен 0. Если Ка больше 0, то имеет место правосторонняя асимметрия, Если Ка меньше 0 - левосторонняя асимметрия. у
2 1 3 х 1- нормальное распределение 2- левосторонняя асимметрия 3- правосторонняя асимметрия 2. Коэффициент эксцесса определяет степень крутизны распределения и определяется на основе соотношения момента четвертого порядка и среднего квадратического отклонения в 4 -й степени:
При Е больше 0 распределение островершинно, при Е меньше 0 - имеет место плосковершинное распределение.
Вопрос 3. Дисперсия обладает рядом свойств: 1. Если из всех значений вариант отнять какое-то постоянное число А, то дисперсия от этого не изменится: s
2. Если все значения вариант разделить на какое-то по постоянное число А, то дисперсия уменьшится от этого в А2 раз, а среднее квадратическое отклонение - в А раз:
3. Если исчислить дисперсию от любой величины А, которая отличается от средней арифметической Исходя из этих свойств, дисперсия для интервального вариационного ряда с равными интервалами определяется по формуле:
где i - величина интервала; m12 - момент первого порядка в квадрате; m2- момент второго порядка. Изучая дисперсию интересующего нас признака, мы не можем определить влияние отдельных факторов, которые характеризуют колеблемость варианта признака. Это можно сделать, разделив изучаемую совокупность на группы, однородные по признаку-фактору, и определив три показателя колеблемости признака в совокупности: 1. Общая дисперсия – она характеризует вариацию признака, которая зависит от всех условий данной совокупности:
где 2. Межгрупповая дисперсия - она отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых (частных) средних около общей средней:
где
fi - численность отдельных групп. 3. Средняя внутригрупповых дисперсий - характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием других, не учитываемых факторов и не зависит от признака-фактора, положенного в основу группировки:
Правило сложения дисперсий: общая дисперсия равна сумме величин межгрупповой дисперсии и средней из внутригрупповых дисперсий:
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.37.68 (0.017 с.) |

 ,
, .
. ,
, .
. ,
, .
. ,
, ;
; .
. ;
; .
. ,
, ;
;






 , где m4 – момент четвертого порядка
, где m4 – момент четвертого порядка .
.
 y
y


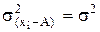 .
. .
. , то эта дисперсия всегда будет больше дисперсии, исчисленной от средней арифметической
, то эта дисперсия всегда будет больше дисперсии, исчисленной от средней арифметической 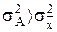 . При этом больше на вполне определенную величину - квадрат разности между средней и условно взятой величиной А, т.е. на
. При этом больше на вполне определенную величину - квадрат разности между средней и условно взятой величиной А, т.е. на  :
: 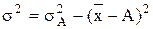 .
. ,
, ,
, - общая средняя для всей изучаемой совокупности.
- общая средняя для всей изучаемой совокупности.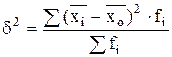 ,
, - средняя по отдельным группам;
- средняя по отдельным группам; .
. .
.


