
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обычно говорят, что при этом функция g(n) является асимптотически точной оценкой функции f(n), Т. К. По определению функция f(n) не отличается от функции g(n) с точностью до постоянного множителя.
Отметим, что из f(n) = Примеры: 1) f(n)=4 2) f(n)= 2. Оценка О (О большое) В отличие от оценки
Вообще, запись O(g(n)) обозначает класс функций, таких, что все они растут не быстрее, чем функция g(n) с точностью до постоянного множителя, поэтому иногда говорят, что g(n) мажорирует функцию f(n). Например, для всех функций: f(n)=1/n, f(n)= 12, f(n)=3*n+17, f(n)=n*Ln(n), f(n)=6* Указывая оценку О есть смысл указывать наиболее «близкую» мажорирующую функцию, поскольку например для f(n)= 3. Оценка В отличие от оценки О, оценка
Например, запись Асимптотическое обозначение О восходит к учебнику Бахмана по теории простых чисел (Bachman, 1892), обозначения Отметим, что не всегда для пары функций справедливо одно из асимптотических соотношений, например для f(n)= В асимптотическом анализе алгоритмов разработаны специальные методы получения асимптотических оценок, особенно для класса рекурсивных алгоритмов. Очевидно, что 8. Элементарные операции в языке записи алгоритмов. Достаточно распространенным способом представления алгоритма является его запись на алгоритмическом языке, представляющем в общем случае систему обозначений и правил для единообразной и точной записи алгоритмов и исполнения их. Отметим, что между понятиями «алгоритмический язык» и «языки программирования» есть различие; прежде всего, под исполнителем в алгоритмическом языке может подразумеваться не только компьютер, но и устройство для работы «в обстановке». Программа, записанная на алгоритмическом языке, не обязательно, предназначена компьютеру. Практическая же реализация алгоритмического языка - отдельный вопрос в каждом
конкретном случае. Как и каждый язык, алгоритмический язык имеет свой словарь. Основу этого словаря составляют слова, употребляемые для записи команд, входящих в систему команд исполнителя того или иного алгоритма. Такие команды называют простыми командами. В алгоритмическом языке используют слова, смысл и способ употребления которых задан раз и навсегда. Эти слова называют служебными. Использование служебных слов делает запись алгоритма более наглядной, а форму представления различных алгоритмов – единообразной. Алгоритм, записанный на алгоритмическом языке, должен иметь название. Название желательно выбирать так, чтобы было ясно, решение какой задачи описывает данный алгоритм. Для выделения названия алгоритма перед ним записывают служебное слово АЛГ (АЛГоритм). За названием алгоритма (обычно с новой строки) записывают его команды. Для указания начала и конца алгоритма его команды заключают в пару служебных слов НАЧ (НАЧало) и КОН (КОНец). Команды записывают последовательно. Приведем последовательность записи алгоритма: АЛГ название алгоритма НАЧ Серия команд алгоритма КОН Например, алгоритм, определяющий движение исполнителя-робота, может иметь вид: АЛГ в_склад НАЧ ВПЕРЕД ВПРАВО ВПРАВО ВПЕРЕД ВПЕРЕД КОН При построении новых алгоритмов могут использоваться алгоритмы, составленные ранее. Алгоритмы, целиком используемые в составе других алгоритмов, называют вспомогательными алгоритмами. Вспомогательным может оказаться любой алгоритм из числа ранее составленных. Не исключается также, что вспомогательным в определенной ситуации может оказаться алгоритм, сам содержащий ссылку на вспомогательные алгоритмы. Очень часто при составлении алгоритмов возникает необходимость использования в качестве вспомогательного одного и того же алгоритма, который к тому же может быть весьма сложным и громоздким. Было бы нерационально, начиная работу, каждый раз заново составлять и запоминать такой алгоритм для его последующего использования. Поэтому в практике широко используют так называемые встроенные (или стандартные) вспомогательные алгоритмы, т.е. такие алгоритмы, которые постоянно имеются в распоряжении исполнителя. Обращение к таким алгоритмам осуществляется так же, как и к «обычным» вспомогательным алгоритмам. У исполнителя-робота встроенным вспомогательным алгоритмом может быть перемещение в склад из любой точки рабочего поля; у исполнителя - язык программирования Бейсик - это, например, встроенный алгоритм «SIN».
Алгоритм может содержать обращение к самому себе как вспомогательному и в этом случае его называют рекурсивным. Если команда обращения алгоритма к самому себе находится в самом алгоритме, то такую рекурсию называют прямой. Возможны случаи, когда рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение. Такая рекурсия называется косвенной. Пример прямой рекурсии: АЛГ движение НАЧ вперед вперед вправо движение КОН Алгоритмы, при исполнении которых порядок следования команд определяется в зависимости от результатов проверки некоторых условий, называют разветвляющимися. Для их описания в алгоритмическом языке используют специальную составную команду - команду ветвления. Она соответствует блок-схеме "альтернатива" и также может иметь полную или сокращенную формуй. Применительно к исполнителю-роботу условием может быть проверка нахождения робота у края рабочего поля (край не_край); проверка наличия объекта в текущей клетке (есть/нет) и некоторые другие: ЕСЛИ условие ТО серия 1 ИНАЧЕ серия 2 ВСЕ ЕСЛИ условие ТО серия ВСЕ ЕСЛИ край ТО вправо ИНАЧЕ вперед ВСЕ Ниже приводится запись на алгоритмическом языке команды выбора, являющейся развитием команды ветвления: ВЫБОР ПРИ условие 1: серия 1 ПРИ условие 2: серия 2 ..... ПРИ условие N: серия N ИНАЧЕ серия N+1 ВСЕ Алгоритмы, при исполнении которых отдельные команды или серии команд выполняются неоднократно, называют циклическими. Для организации циклических алгоритмов в алгоритмическом языке используют специальную составную команду цикла. Она соответствует блок-схемам типа "итерация" и может принимать следующий вид: ПОКА условие НЦ серия 1 КЦ или НЦ серия 1 ДО условие КЦ В случае составления алгоритмов работы с величинами можно рассмотреть и другие возможные алгоритмические конструкции, например, цикл с параметром или выбор. Подробно эти конструкции будут рассматриваться при знакомстве с реальными языками программирования. В заключение приведем алгоритм, составленный для исполнителя-робота, по которому робот переносит все объекты со склада в левый нижний угол рабочего поля (поле может иметь произвольные размеры): АЛГ до_края НАЧ ПОКА не_край НЦ вперед
КЦ КОН АЛГ в_угол3 НАЧ до_края вправо до_края вправо КОН АЛГ перенос НАЧ в_угол3 ЕСЛИ есть ТО взять в_угол3 установить перенос ИНАЧЕ в_угол3 ВСЕ КОН 9. Трудоемкость алгоритмов и временные оценки. Под трудоемкостью алгоритма А на входе D будем понимать количество элементарных операций, которые учитываются при анализе алгоритма. Под худшим случаем трудоемкости понимают наибольшее количество операций, задаваемых алгоритмом А на всех входах D определенной размерности n. Определим лучший случай трудоемкости, как наименьшее количество операций в аналогичном алгоритме и при той же размерности входа. Средний случай трудоемкости определяется средним количеством операций рассматриваемого алгоритма и входных данных. Зависимость трудоемкости алгоритма А от значения параметров на входе D определяет функцию трудоемкости алгоритма А для входа D. Классический анализ алгоритмов в данном контексте связан, прежде всего, с оценкой временной сложности. Большинство алгоритмов имеют основной параметр, который в значительной степени влияет на время выполнения операций. Если же определяющих параметров несколько, то, как правило, один их них выражается как функция от остальных. Иногда используют и такой подход: рассматривают только один параметр, считая остальные константами. Результатом анализа является асимптотическая оценка выполняемых алгоритмом операций в зависимости от длины входа, которая указывает порядок роста функции и результаты сравнения работы алгоритмов для больших данных. При этом оценка на реальных данных отличается от асимптотической тем, что она ориентирована на конкретные длины входов и число выполняемых алгоритмом операций. Временная сложность алгоритма определяется асимптотической оценкой функции трудоемкости алгоритма для худшего случая, обозначается O(f(n)) и читается как "О большое" или "О-нотация". Асимптотический класс функций О включает в себя как средний, так и лучший случай, потому что запись O(f(n)) обозначает класс функций, скорость роста которых не более, чем f(n) с точностью до некоторой положительной константы. В зависимости от вида функции f(n) выделяют следующие классы сложности алгоритмов.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.125.171 (0.026 с.) |
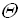 (g(n)) следует, что g(n) =
(g(n)) следует, что g(n) =  +nlnN+174 – f(n)=
+nlnN+174 – f(n)=  : f(n) = 7+1/n =
: f(n) = 7+1/n = 
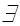 c > 0, n0 > 0: 0 =< f(n) =< c * g(n),
c > 0, n0 > 0: 0 =< f(n) =< c * g(n), 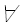 n > n0
n > n0
 (Омега)
(Омега)
 и g(n)=n не выполняется ни одно из асимптотических соотношений.
и g(n)=n не выполняется ни одно из асимптотических соотношений.


