
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гипотеза де-Бройля. Опыт Дэвиссона и Джермера
В 1924 г. французский физик Луи де-Бройль выдвинул гипотезу о том, что дуализм не является особенностью одних только оптических явлений, а имеет универсальный характер. Каждой движущейся микрочастице он поставил в соответствие волновую функцию в виде монохроматической плоской волны. Такая волна характеризуется двумя величинами: частотой w (длиной волны
где Е – полная энергия частицы. Поскольку импульс фотона равен
где р – импульс материальной частицы. Длина волны де-Бройля
Таким образом, волну де-Бройля можно записать в виде
где А – амплитуда; i – мнимая единица; r – радиус-вектор, задающий положение материальной частицы. Функция (9.2) получила название волновой функции,или пси-функции ( Гипотеза де-Бройля вскоре была подтверждена экспериментально. Дэвиссон и Джермер в 1927 г. исследовали отражение электронов от монокристалла никеля, имеющего кристаллическую решетку, принадлежащую к кубической системе. Узкий пучок электронов с одинаковой энергией направлялся на поверхность монокристалла, шлифованную перпендикулярно большей диагонали кристаллической ячейки. Отраженные электроны улавливались цилиндрическим электродом, присоединенным к гальванометру. Интенсивность отраженного пучка оценивалась по силе тока, текущего через гальванометр. Скорость электронов (или ускоряющее напряжение) и угол j варьировались. На рис. 9.1 показаны результаты эксперимента.
Рис. 9.1 Вертикальная ось на графиках определяет направление падающего луча. Сила тока численно равна длине отрезка, проведенного от начала координат до пересечения с кривой. Рассеяние оказалось особенно интенсивным при определенном значении угла j. Этот угол соответствовал отражению от атомных плоскостей, расстояние между которыми d было известно из рентгенографических исследований. При данном j сила тока оказалась особенно значительной при ускоряющем напряжении, равном 54 В.
Вычисленная по формуле (9.1) длина волны, отвечающая этому напряжению, равна 1,67 нм. Полученные результаты совпадали с расчетами, проведенными по формуле Вульфа – Брэгга
Таким образом, опыт Дэвиссона и Джермера подтверждает гипотезу де‑Бройля. Г. П. Томсон (1927 г.) и независимо от него П. С. Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Штерн и сотрудники его лаборатории показали, что дифракционные явления обнаруживаются также у атомных и молекулярных пучков. Во всех перечисленных случаях дифракционная картина соответствует длине волны, определяемой соотношением (9.1). Таким образом, экспериментально было доказано, что все микрочастицы обладают волновыми свойствами.
10. Вероятностный характер волн де-Бройля. Микрочастицами называют элементарные частицы (электрон, протон, фотон и др.), а также сложные частицы, образованные из сравнительно небольшого числа элементарных частиц (молекулы, атомы и др.). Своеобразие свойств микрочастиц отчетливо обнаруживается в следующем мысленном эксперименте.
Рис. 10.1 Направим на преграду с двумя узкими щелями параллельный пучок моноэнергетических (т. е. обладающих одинаковой кинетической энергией) электронов (рис. 10.1). Сначала закроем щель 2, получим изображение 1, затем закроем щель 1, получим изображение 2 (рис. 10.1, б). Если оставить оба отверстия открытыми, получаем картину (рис. 10.1, в). Она оказывается аналогичной картине, получающейся при интерференции двух когерентных световых волн. Характер картины свидетельствует о том, что на движение электрона оказывают влияние оба отверстия. Такой результат несовместим с представлением о траектории. Если бы электрон в каждый момент времени находился в определенной точке пространства и двигался по определенной траектории, он проходил бы через определенное отверстие, первое или второе. Картина, показанная на рис. 10.1, в, указывает на наличие волновых свойств у микрочастиц. Интерференция электронов на двух щелях наблюдалась в эксперименте, проведенном К. Иенссоном в 1961 г.
Немецкий физик Макс Борн предложил рассматривать интенсивность световой волны, или волны де-Бройля, как меру вероятности обнаружения частицы в данном месте пространства. Пусть dV – некоторый объем в пространстве, в котором находится частица, dP – вероятность нахождения частицы в этом объеме, тогда
где Движущейся микрочастице ставится в соответствие волновая функция Рассмотрим принцип суперпозиции волновых функций. Если событие может произойти несколькими взаимно исключающими способами (например, двумя), то вероятность этого события представляет собой сумму вероятностей каждого из способов – принцип суперпозиции. В этом случае результирующая волновая функция
Воспользуемся стандартным обозначением: величина со звездочкой обозначает комплексно сопряженную величину. Тогда плотность вероятности равна
Этот формализм составляет основу волновой и квантовой механики. Приведенное выражение совпадает с правилом сложения амплитуд волн в оптике. При такой вероятностной интерпретации поведения микрочастиц понятие траектории теряет свой строгий смысл. С помощью Y‑функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. Вероятностный смысл волновой функции иной, чем в статистической физике. Там предполагается, что частица находится в определенном месте, но из-за большого числа частиц можно составить лишь вероятностное суждение о ее координатах и вычислить вероятность распределения частиц. В доквантовой физике «понять» означало составить себе наглядный образ объекта или процесса. Квантовую физику нельзя понять в таком смысле слова. Всякая наглядная модель неизбежно будет действовать по классическим законам, и поэтому самое правильное, что можно сделать, это отказаться от попыток строить наглядные модели поведения квантовых объектов. Сочетая в себе свойства частицы и волны, микрочастицы «не ведут себя ни как волны, ни как частицы». Отличие микрочастицы от привычной для нас макрочастицы заключается в том, что она не обладает одновременно определенными значениями координаты и импульса, вследствие чего понятие траектории применительно к микрочастице утрачивает смысл. Здесь уместно сформулировать общее правило квантовой физики: всякая попытка узнать что-либо о свойствах микрочастиц, всякий эксперимент с ними обязательно меняют их состояние и их волновую функцию.
Ричард Фейман, удостоенный в 1965 г. Нобелевской премии за приложение квантовой механики к электродинамике, писал: «Быть может, вам все еще хочется выяснить: “А почему это? Какой механизм прячется за этим законом?” Так вот: никому никакого механизма отыскать не удалось. Никто в мире не сможет вам “объяснить” ни на капельку больше того, что “объяснили” мы. Никто не дает вам никакого более глубокого представления о положении вещей. У нас их нет, нет представлений о более фундаментальной механике, из которой можно вывести эти результаты».
Принцип неопределенности В классической механике состояние материальной точки определяется заданием значений координат и импульса. Своеобразие свойств микрочастиц проявляется в том, что не для всех переменных при измерениях получаются определенные значения. Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты х и компоненты импульса
Из (11.1) следует, что, чем меньше неопределенность одной из переменных (х или Соотношение, аналогичное (11.1), имеет место для у и
Соотношение (11.2) называется принципом неопределенности для величин А и В. Это соотношение сформулировал В. Гейзенберг в 1927 г. Утверждение о том, что произведение неопределенностей значений двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка, называется принципом неопределенности. Энергия и время также являются канонически сопряженными величинами
Это соотношение означает, что определение энергии с точностью D Е должно занять интервал времени, равный по меньшей мере Соотношение неопределенности можно проиллюстрировать следующим примером. Попытаемся определить значение координаты х свободно летящей микрочастицы, поставив на ее пути щель шириной D х, расположенную перпендикулярно к направлению движения частицы. До прохождения частицы через щель ее составляющая импульса
Краю центрального дифракционного максимума (первому минимуму), получающемуся от щели шириной D х, соответствует угол j, для которого
Следовательно,
Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени. Подставив в (11.1) вместо
Очевидно, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости и, следовательно, с тем большей точностью применимо понятие траектории. Уже для макрочастицы размером 1 мкм неопределенности значений х и Принцип неопределенности является одним из фундаментальных положений квантовой механики.
Уравнение Шредингера В развитие идеи де-Бройля о волновых свойствах вещества австрийский физик Э. Шредингер получил в 1926 г. уравнение, названное впоследствии его именем. В квантовой механике уравнение Шредингера играет такую же фундаментальную роль, как законы Ньютона в классической механике и уравнения Максвелла в классической теории электромагнетизма. Оно позволяет найти вид волновой функции частиц, движущихся в различных силовых полях. Вид волновой функции или Y-функции получается из решения уравнения, которое выглядит следующим образом
Здесь m – масса частицы; i – мнимая единица; D – оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых производных по координатам
Буквой U в уравнении (12.1) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу. Уравнение Шредингера является основным уравнением нерелятивистской квантовой механики. Оно не может быть выведено из других уравнений. Если силовое поле, в котором движется частица, стационарно (т.е. постоянно во времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера состоит из двух множителей, один из которых зависит только от координат, другой – только от времени
Здесь Е – полная энергия частицы, которая в случае стационарного поля остается постоянной;
В результате получим
Уравнение (12.3) называется уравнением Шредингера для стационарных состояний. В дальнейшем мы будем иметь дело только с этим уравнением и для краткости будем называть его просто уравнением Шредингера. Уравнение (12.3) часто записывают в виде
В квантовой механике большую роль играет понятие оператора. Под оператором подразумевается правило, посредством которого одной функции, обозначим ее
здесь
В этом уравнении символом
Оператор
где
или в векторном виде В разд. 10 мы уже обсуждали физический смысл Y-функции: квадрат модуля Y -функции (волновой функции) определяет вероятность dP того, что частица будет обнаружена в пределах объема dV:
Поскольку квадрат модуля волновой функции равен произведению волновой функции на комплексно сопряженную величину
Тогда вероятность обнаружения частицы в объеме V
Для одномерного случая
Интеграл от выражения (12.5), взятый по всему пространству от
Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, т. е. вероятность достоверного события, которая равна 1. В квантовой механике принимается, что волновая функция допускает умножение на отличное от нуля произвольное комплексное число С, причем
Условие (12.6) называется условием нормировки. Функции, удовлетворяющие этому условию, называются нормированными. В дальнейшем мы всегда будем полагать, что рассматриваемые нами Y-функции являются нормированными. В случае стационарного силового поля справедливо соотношение
т. е. плотность вероятности волновой функции равна плотности вероятности координатной части волновой функции и от времени не зависит. Свойства Y -функции: она должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек) и иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий. В уравнение Шредингера в качестве параметра входит полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения вида
Частица в потенциальной яме Найдем собственные значения энергии и соответствующие им собственные волновые функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме (рис. 13.1, а). Предположим, что частица
Рис. 13.1 может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U = 0 внутри ямы (при 0 £ х £ l) и Рассмотрим стационарное уравнение Шредингера. Поскольку Y-функция зависит только от координаты х, то уравнение имеет вид
За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Следовательно, и функция y за пределами ямы равна нулю. Из условия непрерывности следует, что y должна быть равна нулю и на границах ямы, т. е.
Этому условию должны удовлетворять решения уравнения (13.1). В области II (0 £ х £ l), где U = 0 уравнение (13.1) имеет вид
Используя обозначение
Решение такого уравнения имеет вид
Условию (14.2) можно удовлетворить соответствующим выбором постоянных k и a. Из равенства Далее из равенства
n = 0 исключено, поскольку при этом Из (13.4) получаем
Таким образом получаем, что энергия частицы в потенциальной яме может принимать только дискретные значения. На рис.13.1, б изображена схема энергетических уровней частицы в потенциальной яме. На этом примере реализуется общее правило квантовой механики: если частица локализована в ограниченной области пространства, то спектр значений энергии частицы дискретен, при отсутствии локализации спектр энергии непрерывен. Подставим значения k из условия (13.4) в (13.3) и получим
Для нахождения константы а воспользуемся условием нормировки, которое в данном случае имеет вид
На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно получить, умножив среднее значение
Графики собственных значений функций при различных n изображены на рис. 13.2. На этом же рисунке показана плотность вероятности yy* обнаружения частицы на различных расстояниях от стенок ямы.
Рис. 13.2 Графики показывают, что в состоянии с n = 2 частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, несовместимо с представлением о траектории. Отметим, что, согласно классическим представлениям, все положения частицы в яме равновероятны.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.35 (0.092 с.) |
 В результате развития представлений о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм (двойственность). Наряду с явлениями, которые самым непосредственным образом свидетельствуют о волновой природе света (интерференция, дифракция), имеются и другие явления, столь же непосредственно обнаруживающие его корпускулярную природу (фотоэффект, эффект Комптона).
В результате развития представлений о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм (двойственность). Наряду с явлениями, которые самым непосредственным образом свидетельствуют о волновой природе света (интерференция, дифракция), имеются и другие явления, столь же непосредственно обнаруживающие его корпускулярную природу (фотоэффект, эффект Комптона).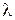 ) и волновым вектором k. Частоту волны для материальной частицы де-Бройль предложил находить из соотношения Эйнштейна
) и волновым вектором k. Частоту волны для материальной частицы де-Бройль предложил находить из соотношения Эйнштейна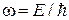 ,
,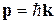 , то волновой вектор можно определить соотношением
, то волновой вектор можно определить соотношением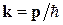 ,
,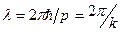 . (9.1)
. (9.1)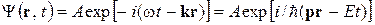 , (9.2)
, (9.2) -функции). Физический смысл волновой функции в идее де-Бройля оставался неясным.
-функции). Физический смысл волновой функции в идее де-Бройля оставался неясным.
 ;
; 

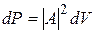 ,
, является плотностью вероятности обнаружения частицы. Отметим, что в оптике под
является плотностью вероятности обнаружения частицы. Отметим, что в оптике под 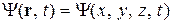 , которая представляет собой функцию координат и времени. Вероятность обнаружить частицу в произвольный момент времени t в любой точке с координатами (х, у, z) пропорциональна
, которая представляет собой функцию координат и времени. Вероятность обнаружить частицу в произвольный момент времени t в любой точке с координатами (х, у, z) пропорциональна 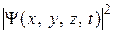 . Квадрат модуля используется потому, что
. Квадрат модуля используется потому, что 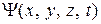 – комплексная функция. Формально она обладает свойствами классической волны, поэтому ее называют волновой функцией.
– комплексная функция. Формально она обладает свойствами классической волны, поэтому ее называют волновой функцией.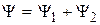 .
.
 . Неопределенности значений х и
. Неопределенности значений х и  . (11.1)
. (11.1) , z и
, z и  , а также для ряда других пар величин (такие пары величин называются канонически сопряженными). Обозначив канонически сопряженные величины буквами А и В, можно написать
, а также для ряда других пар величин (такие пары величин называются канонически сопряженными). Обозначив канонически сопряженные величины буквами А и В, можно написать . (11.2)
. (11.2) .
. .
. , зато координата х частицы является совершенно неопределенной (рис. 11.1).
, зато координата х частицы является совершенно неопределенной (рис. 11.1). В момент прохождения частицы через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность D х, но это достигается ценой утраты определенности значения
В момент прохождения частицы через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность D х, но это достигается ценой утраты определенности значения 
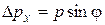 .
. .
.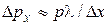 , и получаем
, и получаем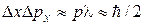 .
. , получим соотношение
, получим соотношение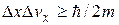 .
.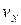 оказываются за пределами точности измерения этих величин, так что ее движение будет практически неотличимо от движения по траектории.
оказываются за пределами точности измерения этих величин, так что ее движение будет практически неотличимо от движения по траектории.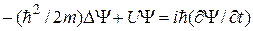 .
.  .
. . (12.2)
. (12.2) – координатная часть волновой функции. Чтобы убедиться в справедливости (12.2), подставим его в (12.1):
– координатная часть волновой функции. Чтобы убедиться в справедливости (12.2), подставим его в (12.1): .
.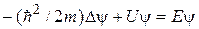 . (12.3)
. (12.3)
 .
. сопоставляется другая функция, обозначим ее f. Символически это записывается следующим образом
сопоставляется другая функция, обозначим ее f. Символически это записывается следующим образом ,
, – символическое обозначение оператора (можно было взять любую другую букву со «шляпкой» над ней, например
– символическое обозначение оператора (можно было взять любую другую букву со «шляпкой» над ней, например  и т. д.). В формуле (12.1) роль
и т. д.). В формуле (12.1) роль  , а роль f – правая часть формулы. Например, символ D означает двукратное дифференцирование по трем координатам, х, у, z, с последующим суммированием полученных выражений. Оператор может, в частности, представлять собой умножение исходной функции
, а роль f – правая часть формулы. Например, символ D означает двукратное дифференцирование по трем координатам, х, у, z, с последующим суммированием полученных выражений. Оператор может, в частности, представлять собой умножение исходной функции  на некоторую функцию U. Тогда
на некоторую функцию U. Тогда  , следовательно,
, следовательно,  . Если рассматривать функцию U в уравнении (12.3) как оператор, действие которого на Y-функцию сводится к умножению
. Если рассматривать функцию U в уравнении (12.3) как оператор, действие которого на Y-функцию сводится к умножению  . (12.4)
. (12.4)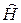 обозначен оператор, равный сумме операторов
обозначен оператор, равный сумме операторов  и U:
и U: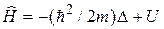 .
.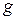 составляется уравнение, аналогичное (12.4). Оно имеет вид
составляется уравнение, аналогичное (12.4). Оно имеет вид ,
, – оператор, сопоставляемый g. Так, например, оператор импульса определяется соотношениями
– оператор, сопоставляемый g. Так, например, оператор импульса определяется соотношениями ;
;  ;
; 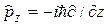 ,
,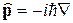 , где Ñ – градиент.
, где Ñ – градиент. , (12.5)
, (12.5)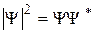 , то
, то .
. .
. .
. до
до  , равняется единице:
, равняется единице:

 (12.6)
(12.6) ,
,
 вне ямы (при х < 0 и х > l).
вне ямы (при х < 0 и х > l). . (13.1)
. (13.1) . (13.2)
. (13.2) .
. , придем к известному из теории колебаний волновому уравнению
, придем к известному из теории колебаний волновому уравнению .
. . (13.3)
. (13.3) получаем
получаем 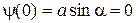 Þ a = 0.
Þ a = 0.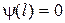 получаем
получаем  . Это условие выполняется при
. Это условие выполняется при (n = 1, 2, 3,...), (13.4)
(n = 1, 2, 3,...), (13.4) (n = 1, 2, 3,...), следовательно,
(n = 1, 2, 3,...), следовательно,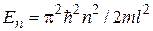 (n = 1, 2, 3,...).
(n = 1, 2, 3,...). .
. .
.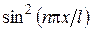 (равное, как известно, 1/2) на длину промежутка. Таким образом, получаем
(равное, как известно, 1/2) на длину промежутка. Таким образом, получаем 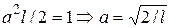 . Окончательно собственные волновые функции имеют вид
. Окончательно собственные волновые функции имеют вид (n = 1, 2, 3,...).
(n = 1, 2, 3,...).



