
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вейвлет-разложение как способ представления речевого сигнала
Рассмотрим сигнал как значения непрерывной функции времени Если конструировать базис функционального пространства
то на его основе можно записать интегральное вейвлет-преобразование
Результатом вейвлет-преобразования сигнала является двумерный массив амплитуд - значений коэффициентов W (a, b) [102-104, 106]. Распределение этих значений в пространстве (a, b) = (временной масштаб, временная локализация) дает информацию об эволюции относительного вклада компонент разного масштаба во времени и называется вейвлет-спектром. Введя аналог частоты Если вейвлет
также нормированы на единицу, т. е.
Вейвлет Вейвлеты покрывают все пространство, используя смещение по-разному сжатых вариантов единственной функции, следовательно, любую функцию из
Признаки вейвлета Для практического применения важно знать признаки, которыми обязательно должна обладать функция, чтобы быть вейвлетом: Локализация. Вейвлет должен быть локализован и во временном пространстве, и по частоте. Нулевое среднее:
Часто для приложений оказывается необходимым, чтобы первые
Такой вейвлет называется вейвлетом Ограниченность:
Опишем сигнал в терминах вейвлет-преобразования при помощи его средних (по некоторым интервалам) значений и изменений вокруг этих средних (флуктуациями). Это позволит вскрыть флуктуационную структуру сигнала на разных масштабах, что приводит к понятию многомасштабного анализа.
Многомасштабный анализ Многомасштабное приближение 1. 2. 3. 4. С учетом многомасштабного анализа разложение функции в вейвлет-ряд имеет вид:
при этом Возвращаясь к вейвлетам, отметим, что Вейвлет-коэффициенты
Первая сумма в (1) со скейлинг-функциями
Представление (2.14) взаимно однозначно для любой функции из Вейвлеты Добеши Свяжем функцию
Величина масштабирующего множителя определяет размер ячеек выбранной решетки, число
Если
В практических приложениях используются только вейвлет-коэффициенты Общие свойства скейлинг-функций и вейвлетов однозначно определяют коэффициенты Из свойства ортогональности масштабных функций:
Из ортогональности вейвлетов масштабным функциям:
Отсюда получим
т. е. Условие ортогональности вейвлетов полиномам до степени
Вообще говоря, чем больше моментов равны нулю, тем больше вейвлет-коэффициентов для гладких функций близки к нулю. Очевидно, число нулевых моментов важно для достижения более сильного сжатия сигнала. Условие нормировки:
Набор всех возможностей (2.17) - (2.20) задает полную систему вейвлетов данного порядка из известного семейства ортонормальных вейвлетов Добеши. Вейвлеты Добеши с компактным носителем определяются однозначно для данного многомасштабного анализа с точностью до сдвига аргумента (смещения). После того, как выбран определенный вейвлет, т. е. коэффициенты Быстрое вейвлет-преобразование В реальных ситуациях с оцифрованным сигналом мы имеем дело с конечным набором цифр (точек). Поэтому всегда существует наилучший уровень разрешения, когда каждый интервал содержит по одному числу. Припишем значение Многомасштабный анализ приводит естественным путем к иерархической и быстрой схеме вычисления вейвлет-коэффициентов заданной функции. В общем случае итерационные формулы быстрого вейвлет-преобразования имеют вид:
с Эти уравнения обеспечивают быстрые (так называемые пирамидальные) алгоритмы вычисления вейвлет-коэффициентов. Начав с Лекция 3 Тема. Способы параметризации речевого сигнала (продолжение) На лекции будет рассмотрено: Основы теории речеобразования. Гомоморфная обработка сигналов. Кодирование речевых сигналов на основе линейного предсказания. Перцептуальное кодирование.
|
|||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 57; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.63.87 (0.023 с.) |
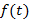 . Очевидно, что
. Очевидно, что  - локализована, т. е. f Î
- локализована, т. е. f Î 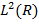 .
.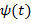 с произвольными значениями базисных параметров – масштабного коэффициента a и параметра сдвига b:
с произвольными значениями базисных параметров – масштабного коэффициента a и параметра сдвига b: , a,b Î R, y Î
, a,b Î R, y Î 
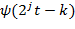 , где j и k – целые числа, с помощью дискретных масштабных преобразований
, где j и k – целые числа, с помощью дискретных масштабных преобразований 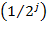 и сдвигов
и сдвигов 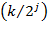 мы можем описать все частоты и покрыть всю ось, имея единственный базисный вейвлет
мы можем описать все частоты и покрыть всю ось, имея единственный базисный вейвлет 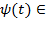
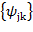 вида
вида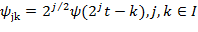


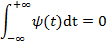
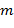 моментов были равны 0:
моментов были равны 0: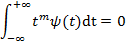
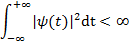
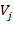 замкнутых линейных пространств
замкнутых линейных пространств 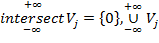 всюду плотно в
всюду плотно в 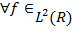 и
и 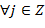
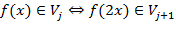 ;
;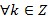
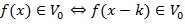 ;
;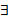 такая функция
такая функция 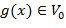 что последовательность
что последовательность 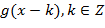 является ортонормальным базисом Рисса в пространстве
является ортонормальным базисом Рисса в пространстве 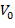 .
.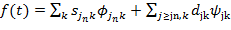 (2.14)
(2.14)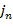 является уровнем детализации,
является уровнем детализации, 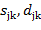 - коэффициенты вейвлет-разложения,
- коэффициенты вейвлет-разложения, 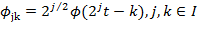 ,
, 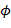 - скейлинг-функция или масштабная функция,
- скейлинг-функция или масштабная функция, 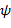 - базисный или «материнский» вейвлет. Эти коэффициенты зачастую называют суммами (
- базисный или «материнский» вейвлет. Эти коэффициенты зачастую называют суммами (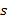 ) и разностями (
) и разностями (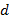 ), связывая со средними значениями и флуктуациями соответственно.
), связывая со средними значениями и флуктуациями соответственно.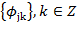 образуют ортонормированный базис
образуют ортонормированный базис 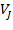 ;
; 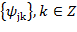 образуют ортонормированный базис в
образуют ортонормированный базис в 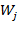 , где
, где 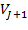 . Полный набор
. Полный набор 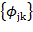 и
и 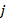 образуют ортонормированный базис в
образуют ортонормированный базис в 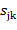 и
и 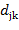 можно вычислить по формулам:
можно вычислить по формулам: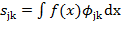 (2.15)
(2.15)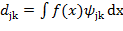 (2.16)
(2.16)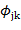 содержит средние значения
содержит средние значения 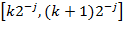 (усреднение проводится с весовыми функциями
(усреднение проводится с весовыми функциями  -том отрезке). Второй член содержит все флуктуации
-том отрезке). Второй член содержит все флуктуации  , где
, где 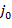 - начальный уровень с наименьшими интервалами, число членов в каждой сумме зависит от выбранного уровня разрешения. На
- начальный уровень с наименьшими интервалами, число членов в каждой сумме зависит от выбранного уровня разрешения. На 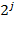
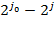
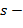 коэффициенты и получается представление скейлинг-функцией, конечное представление улавливает все флуктуации, имеющиеся в сигнале. При практическом анализе сигналов скейлинг- и вейвлет-функции называют широкополосными и узко-полосными фильтрами, т. к. они отфильтровывают компоненты сигнала на больших и малых масштабах.
коэффициенты и получается представление скейлинг-функцией, конечное представление улавливает все флуктуации, имеющиеся в сигнале. При практическом анализе сигналов скейлинг- и вейвлет-функции называют широкополосными и узко-полосными фильтрами, т. к. они отфильтровывают компоненты сигнала на больших и малых масштабах.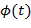 с ее сдвинутыми и сжатыми модификациями. Простейшее линейное соотношение с числом коэффициентов
с ее сдвинутыми и сжатыми модификациями. Простейшее линейное соотношение с числом коэффициентов 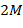 можно записать в виде:
можно записать в виде: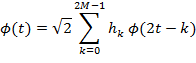
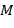 - число коэффициентов
- число коэффициентов 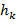 и длину области задания вейвлета. Для ортонормированных базисов
и длину области задания вейвлета. Для ортонормированных базисов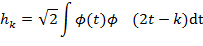
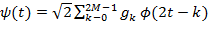 , где
, где 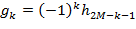 . Связь
. Связь 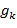 и
и 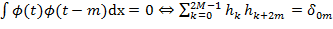 (2.17)
(2.17)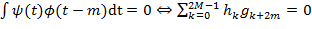
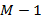 :
: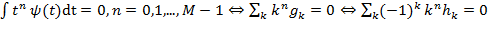 (2.19)
(2.19)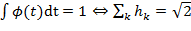 (2.20)
(2.20) и
и  , можно проводить вейвлет-преобразование сигнала
, можно проводить вейвлет-преобразование сигнала  этому уровню разрешения.
этому уровню разрешения.
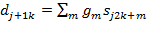
 .
. , мы вычислим все другие вейвлет-коэффициенты при известных
, мы вычислим все другие вейвлет-коэффициенты при известных  из доступного набора данных в виде коэффициентов
из доступного набора данных в виде коэффициентов 


