Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
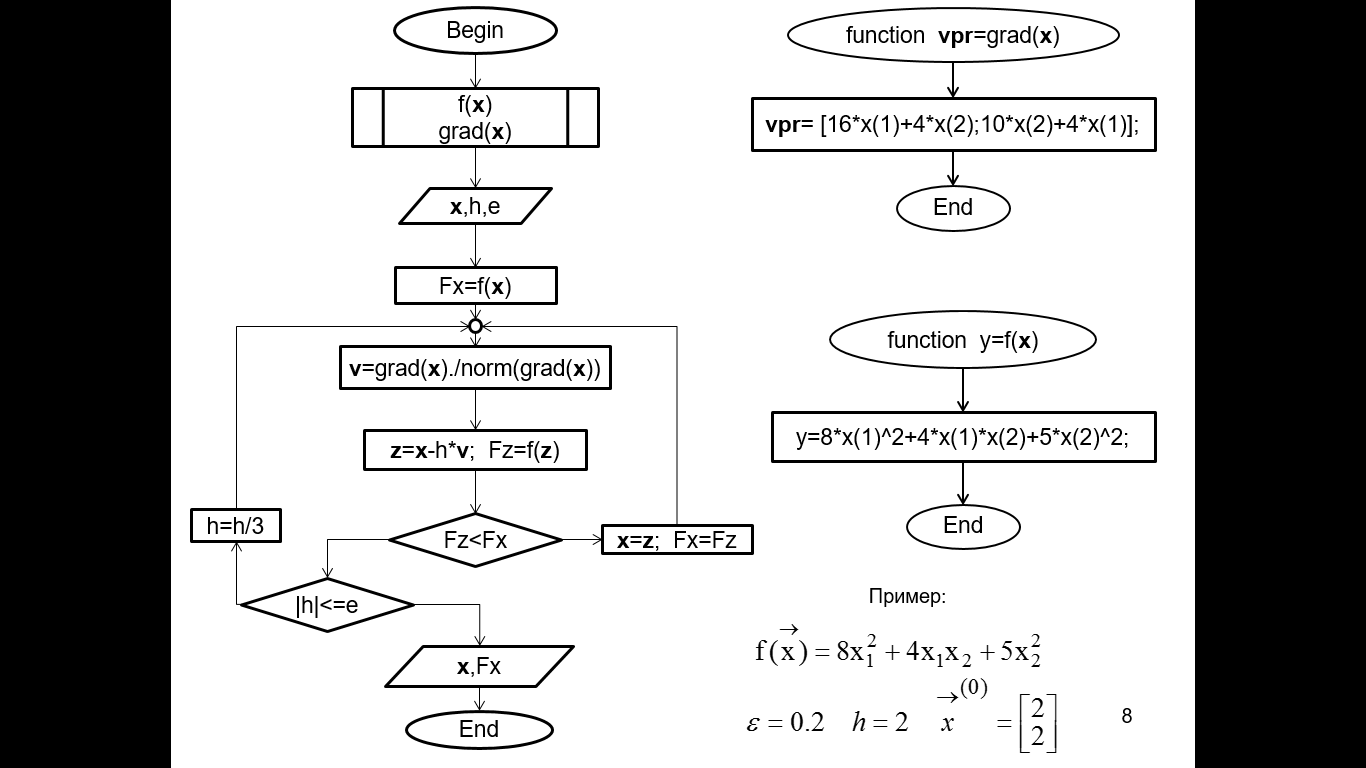
Блок-схема. Многомерная оптимизация. Градиентный метод.
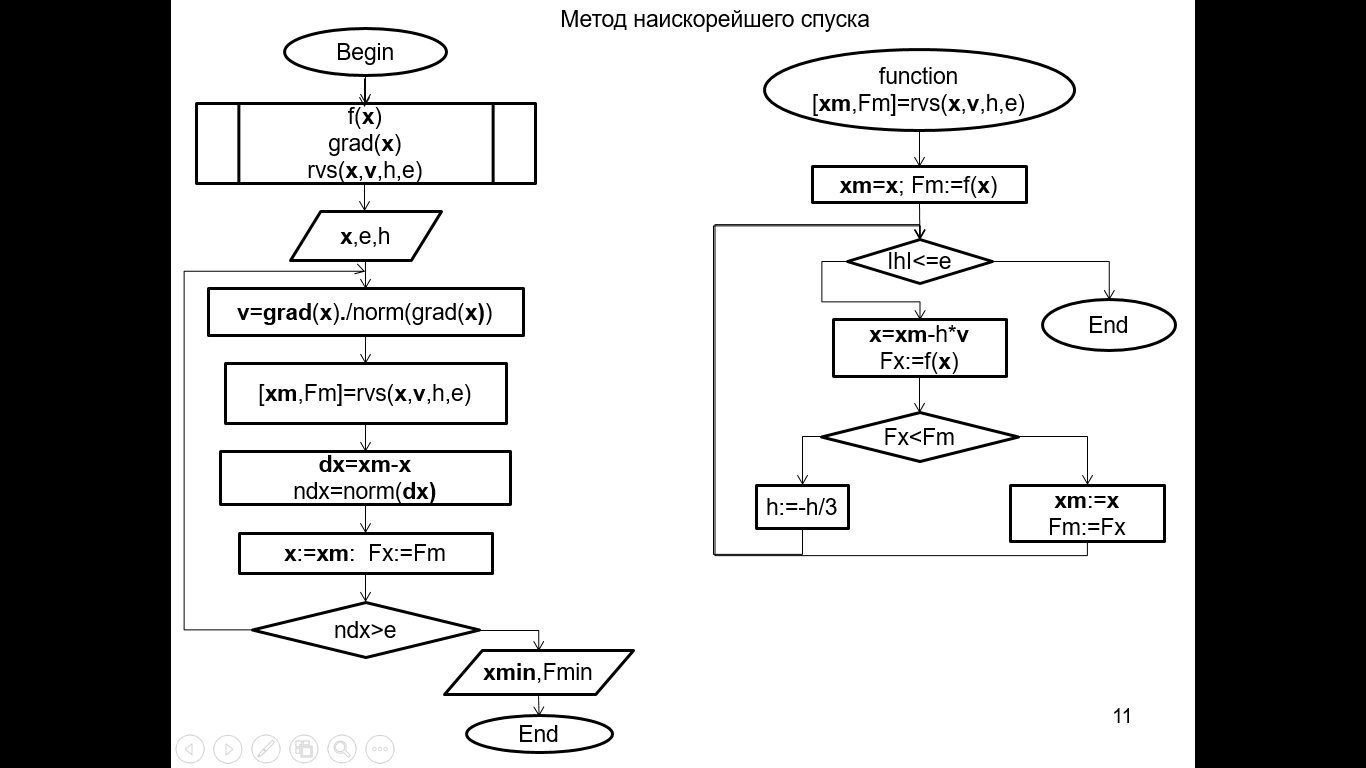
Блок-схема. Многомерная оптимизация. Метод наискорейшего спуска.
Симплексный метод. Симплексом в n-мерном пространстве называется выпуклый многоугольник с n+1 вершиной. n=2 треугольник n=3 тетраэдр. Рис. 2.10.5. Тетраэдр.
Алгоритм 1) Дана функция 2x переменных 2) Вычисляем координаты вершин симплекса
3) Вычисляем значения функции 4) Определяем (рис.2.10.6) худшую вершину
Рис.2.10.6. Переход от худшей вершины к отраженной. 5) Сравниваем значения функции 6) Условие выполняется. За новый симплекс принимаем симплекс с вершиной 7) Условие не выполняется. Проверяем условие окончания h< ε 8) Условие окончания выполняется. Выводим координаты и значение функции лучшей вершины 9) Условие не выполняется. За
Операторы МАТЛАБа позволяют это сделать так: fxx=inline(‘8*x(1)^2+5*x(2)^2+4x(1)*x(2)') [x,y,opt]=fminsearch(fxx,[0;0])
Метод сканирования. В области исследуемой функции двух переменных выбирается значение одной из переменных, соответствующее краю области поиска. По другой переменной интервал поиска разбивается на равные участки, длина каждого из которых равна шагу поиска. Далее значение функции последовательно определяется во всех точках разбиения и на краях отрезка, наименьшее из них запоминается. Затем увеличивают переменную, значение которой было постоянным, на шаг поиска и повторяют процедуру. И так до тех пор, пока не будет исследована вся область поиска с заранее выбранным шагом по каждой из переменных. Минимальное из всех сохраненных значений минимумов и есть глобальный минимум. Для повышения точности повторяют сканирование в области, края которой отстоят от найденной точки минимума на величину шага предыдущего сканирования. Новое значение шага сканирования будет многократно меньше.
Метод Гаусса-Зейделя. Движение к оптимуму происходит поочередно по каждой из осей до нахождения частного экстремума (ниже на рис.2.10.2). После нахождения частного экстремума по одной из осей начинается поиск экстремума по другой оси до частного минимума при условии, что значение первой переменной равно найденному минимуму (максимуму) на первой оси. И так поочередно. Процесс последовательно продолжается до тех пор, пока не будет достигнута заданная точность локализации экстремума, т. е. если шаг по каждой из осей приводит к возрастанию (уменьшению) функции, а величина шага меньше или равна заданной точности поиска, то расчет закончен.
Рис.2.10.7. Движение до достижения экстремума по одной оси. Метод пробных движений. По каждой из переменных: · из исходной точки делается маленький пробный шаг; · находится значение функции; · шаг делается обратно, чтобы вернуться в исходную точку. Из всех опробованных направлений выбирается то, в котором уменьшение (увеличение) целевой функции наибольшее. Делается шаг (возможно, больше пробного) в выбранном таким образом направлении. Процедура повторяется до достижения заданной точности поиска.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 34; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.197.164 (0.005 с.) |
||||||||||||||||
 точность ε, параметр h, начальное приближение
точность ε, параметр h, начальное приближение 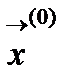
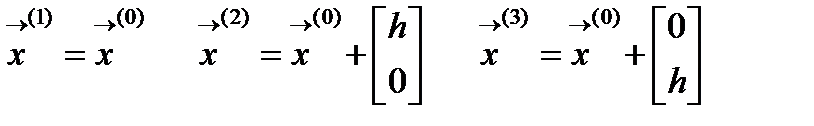
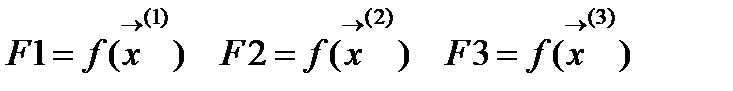
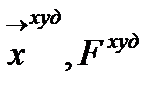 и координаты отраженной вершины, она будет лежать на прямой исходящей из худшей вершины и проходящей через середину противоположной грани
и координаты отраженной вершины, она будет лежать на прямой исходящей из худшей вершины и проходящей через середину противоположной грани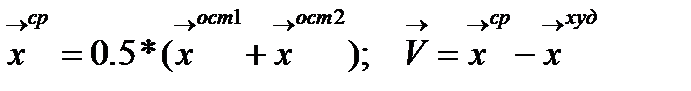
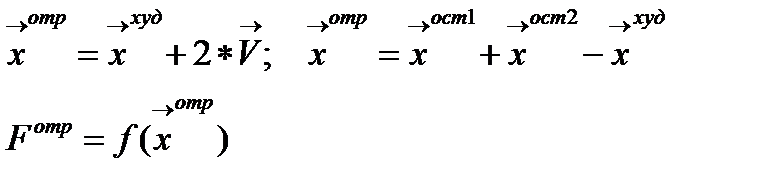
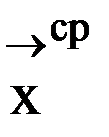

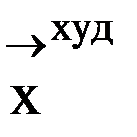
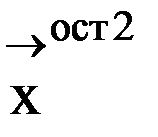
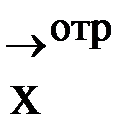
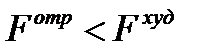
 и повторяем с пункта 3
и повторяем с пункта 3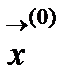 принимаем лучшую вершину последнего симплекса, уменьшаем длину грани h=h/3 и повторяем с пункта 2.
принимаем лучшую вершину последнего симплекса, уменьшаем длину грани h=h/3 и повторяем с пункта 2.