
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мэ. Решения. 11 класс. 2017год ⇐ ПредыдущаяСтр 5 из 5
1. Из первого равенства получаем f((x+2017)+2017) = f(2017 – (x+2017)) = f(-x), а из второго f((x+2018)+2018) = f(2018 – (x+2018)) = f(-x). При произвольном x правые части приведённых равенств совпадают, следовательно, равны и левые: f(x + 4034) = f(x+4036). Заменив переменную x = y – 4034, получим, что при произвольном действительном y выполнено равенство f(y) = f(y+2). Поскольку функция f(y) определена при всех действительных y, из этого равенства следует, что число 2 является её периодом. 2. Для x допустимы значения
Поскольку левая часть полученного равенства не отрицательна, правая тоже должна быть не отрицательной. Таким образом, равенство может быть выполнено, только если Ответ: [1; 2]. 3. Проведём описанную окружность треугольника АВС и зафиксируем направление её обхода при движении A → B → C → A. При перемещении одной из шайб в противоположную полуплоскость относительно прямой, проходящей через две другие точки, направление обхода такой окружности меняется: если сначала направление обхода было по часовой стрелке, то после перемещения одной шайбы оно становится против часовой стрелки и наоборот. За 25 ходов произойдёт 25 смен направления. Так как число 25 нечётное, в результате направление обхода описанной окружности изменится. Следовательно, шайбы не могут вернуться на свои места. Ответ: нет.
Ответ: Да. 5. Покажем, что число братьев должно равняться числу сестёр. Пусть имеется m братьев и n сестёр. Поскольку сейчас все братья в ссоре с разным числом сестёр, значит, есть хотя бы одна пара, которая всё ещё находится в ссоре. Поскольку сейчас каждая сестра находится в ссоре с одним и тем же числом братьев, значит каждая в ссоре хотя бы с одним из них, и час назад она с этим братом тоже была в ссоре. Но час назад сёстры были в ссоре с разным числом братьев. Обозначим ai число братьев, бывших в ссоре с i-й сестрой час назад. Все числа a1, …, an – это различные натуральные числа, не превосходящие m., следовательно, n ≤ m (число сестёр не больше, чем число братьев).
С другой стороны, час назад каждая сестра была в ссоре с разным числом братьев, следовательно, одна из сестёр не была в ссоре хотя бы с одним братом. Братья же были в ссоре с одинаковым числом сестёр, значит, каждый не был в ссоре хотя бы с одной из них. После примирения число ссорящихся пар уменьшилось, и теперь по-прежнему каждый из братьев не в ссоре хотя бы с одной из сестёр. Обозначим bj число сестёр, с которыми находится в ссоре брат с номером j. Числа b1, …, bm – различные целые не отрицательные числа, не превосходящие n – 1, следовательно, m ≤ n (число братьев не больше, чем число сестёр). Утверждение доказано, равенство m = n является истинным. Осталось найти возможные значения для числа m = n. Как видно из предыдущего рассуждения, час назад была сестра, которая была в ссоре ровно с одним братом. Значит, после примирения каждая из сестёр находится в ссоре ровно с одним братом. Общее число ссорящихся пар равно n. И при этом число ссорящихся пар равно n = 0 + 1 + … + (n – 1), откуда n = 3. Приведём пример, показывающий, что такая ситуация возможна. Обозначим братьев буквами A, B, C, а сестёр – цифрами 1, 2, 3. Запись вида A3 будет означать, что брат A в ссоре с сестрой 3. Пусть множество пар в ссоре час назад было {A1, A3, B2, B3, C2, C3}, а после примирения – {A1, C2, C3}. Легко видеть, что в этом примере условия выполняются. Замечание. Если дан только ответ без обоснования, 0 баллов. Если приведён пример без доказательства равенств m = n = 3, 1 балл.
|
|||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 36; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.138.123 (0.006 с.) |
 . Обозначим
. Обозначим 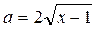 . Возводя в квадрат обе части уравнения и выполняя преобразования, получим:
. Возводя в квадрат обе части уравнения и выполняя преобразования, получим: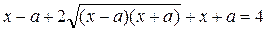 ;
;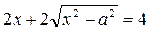 ;
;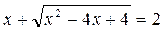 ;
;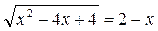 .
.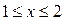 . Вновь, возводя в квадрат, получим равенство:
. Вновь, возводя в квадрат, получим равенство:  , истинное при всех допустимых значениях x.
, истинное при всех допустимых значениях x.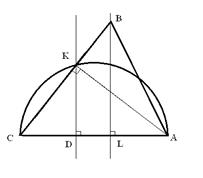 4. Покажем, как можно построить требуемый треугольник. Построим на плоскости произвольно отрезок CA, на нём выберем точку L так, что выполнено равенство
4. Покажем, как можно построить требуемый треугольник. Построим на плоскости произвольно отрезок CA, на нём выберем точку L так, что выполнено равенство 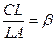 , и на отрезке CL выберем точку D так, что
, и на отрезке CL выберем точку D так, что 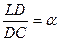 . В точках L и D построим перпендикуляры к AC: прямую p ^ AC через точку L и прямую q ^ AC через точку D. Окружность w с диаметром AC пересекает прямую q в двух точках. Обозначим одну из них K. Пусть B – точка пересечения прямых p и CK. По теореме Фалеса
. В точках L и D построим перпендикуляры к AC: прямую p ^ AC через точку L и прямую q ^ AC через точку D. Окружность w с диаметром AC пересекает прямую q в двух точках. Обозначим одну из них K. Пусть B – точка пересечения прямых p и CK. По теореме Фалеса 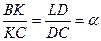 . Угол AKC – прямой, как вписанный угол, опирающийся на диаметр. Отрезок AK является высотой. Поскольку точка пересечения высот треугольника ABC находится внутри треугольника, он – остроугольный. Следовательно, треугольник ABC – искомый.
. Угол AKC – прямой, как вписанный угол, опирающийся на диаметр. Отрезок AK является высотой. Поскольку точка пересечения высот треугольника ABC находится внутри треугольника, он – остроугольный. Следовательно, треугольник ABC – искомый.


