
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числові характеристики неперервних випадкових величин.
Математичне сподівання (очікування) неперервної величини
M(x)= Де f(x) – щільність розподілу.
Дисперсія.
Середнє квадратичне відхилення
Нормальний закон розподілу Ймовірність того,що випадкова величина прийме значення, що належить інтервалу (α;β), обчислюється за формулою:
Де Ф(х)- функція Лапласа, дивись додаток 2 Ф(-х)=-Ф(х)
а – математичне сподівання, тобто середнє значення.
1.9 Ймовірність того, що абсолютна величина відхилення менше додатного числа ξ (епсілон), обчислюється за формулою:
Р(│х-а│<ξ)=2Ф( Розв’язування типових задач 2.1 Пристрій складається з трьох елементів, ймовірність відмови кожного елемента в одному іспиті дорівнює 0,1. Скласти закон розподілу числа елементів в одному іспиті. Розв'язання Дискретна випадкова величина Х має слідуючи можливі значення: Х1=0 (ні один з елементів пристрою не відмовив) Х2=1 (відмовив один елемент) Х3=2 (відмовили два елементи) Х4=3 (відмовили три елементи) Ймовірність відмови кожного елемента дорівнює 0,1, тоді q=1-0,1=0,9. За формулою Бернулі розрахуємо ймовірність всіх можливих випадків:
Запишемо біноміальний закон розподілу:
Таблиця 2.1.1 Біноміальний закон розподілу:
Контроль: 0,729+0,243+0,027+0,001=1 Знайдемо математичне сподівання:
Знайдемо дисперсію випадкової величини:
М(х2)= 02 0,729+12 0,243+22 0,027+32 0,001 = 0,243+4 0,027+9 0,001= 0,243+0,108+0,009=0,360
Д(х)=0,36-(0,4)2=0,36-0,16=0,2
Знайдемо середнє квадратичне відхилення:
Побудуємо полігон ймовірності:
Малюнок 1 Полігон ймовірності Задача 2.2 Знайти дисперсію випадкової величини Х, заданої функцією розподілу:
F(х)
Розв’язання
D(Х)
Знайдемо щільність розподілу
f(x)=
Знайдемо математичне очікування:
М(х)
Знайдемо дисперсію:
Відповідь: Задача 2.3
0, якщо х £ -1 F(х) = Ах +В, якщо –1 < х £ 3 1, якщо х > 3 2.3.1 Знайти параметри А і В 2.3.2 Накреслити графік у = F(х) 2.3.3 Визначити ймовірність, що випадкова величина Х Î [1;5]
2.3.4 Обчислити математичне сподівання і дисперсію заданої випадкової величини. Розв’язання: 2.3.1 Користуючись властивістю інтегральної функції:
Тоді
2.3.2 Графік F(x)
2.3.3 Р(1 £ х £ 5) = F(5) - F(1) = 1- 2.3.4 Знайдемо щільність розподілу
f(x) = F¢(x)=
Математичне сподівання: М(х)=
Дисперсія: D (х) =
Задача 2.4
Середня вага риби однієї породи та одного віку 375 гр., відхилення ваги характеризується середнім квадратичним відхиленням 2.4.1 ймовірність того, що вага спійманої риби однієї породи буде обмежена від 325 гр. до 425 гр.; 2.4.2 вагу, яка не перевищує спіймана риба із ймовірністю р=0,9960 Розв’язання: 2.4.1 Р α = 325 см β = 425 см σ =25 см а =375-математичне сподівання
Підставимо значення у формулу Р(325 < х < 425) = Ф( = Ф( Відповідь: р = 0,95
2.4.2 Знайти вагу, яка не перевищує спіймана риба із ймовірністю р=0,9960, тобто треба із формули ймовірності того, що абсолютна величина відхилення менша числа x (епсілон).
Розв’язання
Знайдемо x. за формулою Р маємо: 0,9960= 2Ф поділимо обидві частини на 2, отримаємо: 0,4980=Ф
Питання до самоконтролю 3.1 Дайте означення випадкової величини. 3.2 Сформулюйте закон розподілення випадкової величини. 3.3 Дайте визначення математичного сподівання та дисперсії. 3.4 Дайте означення функції розподілу випадкової величини. 3.5 Запишіть формули за допомогою яких обчислюються числові характеристики неперервних випадкових величин. 3.6 Запишіть формулу обчислення ймовірності того, що випадкова величина прийме значення з інтервалу ( Індивідуальні завдання до самостійної роботи №3 Задача №1 Задано закон розподілення випадкової величини Х. Знайти: 1.1 математичне сподівання М(х); 1.2 дисперсію D(x); 1.3 Середнє квадратичне відхилення. 1.4 Побудувати полігон.
Таблиця 1 Індивідуальні завдання до задачі №1
Задача №2 Задана інтегральна функція розподілу випадкової неперервної величини.
Знайти: 2.1 знайти параметри А і В; 2.2 визначити ймовірність,що випадкова величина належить х є (m1;m2); 2.3 обчислити математичне сподівання і дисперсію заданої випадкової величини.
Таблиця 2 Індивідуальні завдання до задачі №2
Задача №3 Середня вага риби однієї породи та одного віку Визначити: 3.1 Ймовірність того, що вага спійманої риби однієї пороли буде обмежена від m1 до m2 3,2 Вагу, яку не перевищує спіймана риба з ймовірністю р.
Таблиця №3 Індивідуальні завдання до задачі №3
Самостійна робота №4 (10 годин)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 680; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.229.113 (0.055 с.) |
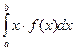 , 1.6.1
, 1.6.1 1.6.2
1.6.2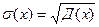 1.7.1
1.7.1 1.8.1
1.8.1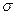 - середнє квадратичне відхилення,
- середнє квадратичне відхилення,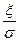 ) 1.9.2
) 1.9.2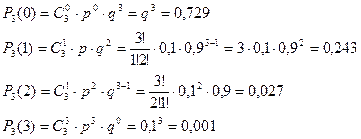
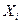
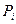
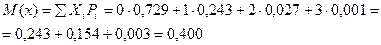
 2.1.1
2.1.1

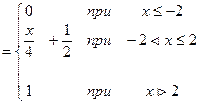



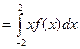 =
= 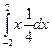 =
= 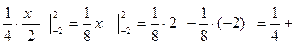
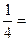
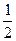
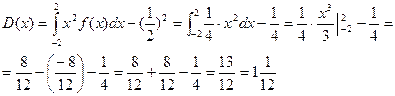
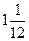
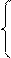 Задана інтегральна функція розподілу випадкової неперервної величини
Задана інтегральна функція розподілу випадкової неперервної величини ,
, 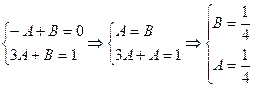


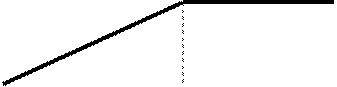

 -1 3 х
-1 3 х =
= 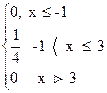
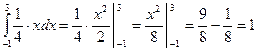
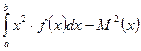
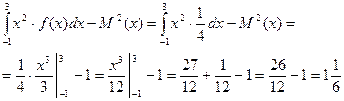
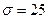 .Визначити:
.Визначити:
 )-Ф(
)-Ф( ) =
) =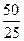 ) - Ф(
) - Ф( ) = Ф(2)+Ф(2) = 0,4772+0,4772 = 0,9544
) = Ф(2)+Ф(2) = 0,4772+0,4772 = 0,9544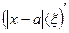 = 2 Ф
= 2 Ф 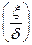 ,
,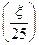 ,
,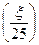 , із таблиці “додаток 2”, знайдемо
, із таблиці “додаток 2”, знайдемо 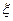 .
.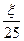 = 2,88,
= 2,88, 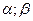 ).
).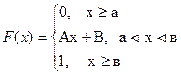
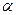 , відхилення ваги характеризується середнім квадратичним відхиленням
, відхилення ваги характеризується середнім квадратичним відхиленням 


