
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила. Система сил. Равновесие тела.Стр 1 из 6Следующая ⇒
Сила. Система сил. Равновесие тела. Равновесие – состояние покоя по отношению к другим телам, например к Земле. Равновесие жидких и газообразных тел рассматривается в курсах гидростатики и аэростатики. Прямая, по которой направлена сила, назыв. линией действия силы. Система сил – совокупность сил, действующих на рассматриваемое тело. Если линии действия всех сил лежат в одной плоскости, система сил называется плоской, а если линии действия сил лежат не в одной плоскости, - пространственной. Существуют сходящиеся и параллельные линии действия сил. Тело, которому из данного положения можно сообщить любое перемещение в пространстве – свободное. Если заменить систему сил другой, при этом не изменяя состояние покоя или движения, - эквивалентная система сил. Если под действием сил тело находится в покое, то система сил называется уравновешенной или эквивалентной 0. Если система сил = одной силе, то она равнодействующая. Имеющая противоположное направление – уравновешивающая. Внешние силы – силы со стороны других тел, внутренние – силы, с которыми части данного тела действуют друг на друга. Сила, приложенная к одной точке – сосредоточенная. Уравновешенные силы: Система сил, под действием которой свободное твердое тело может находится в покое, называется уравновешенной.
Система сходящихся сил. Сходящимися называются силы, линии действия которых пересекаются в одной точке. Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в точке их пересечения
Проекции равнодействующей системы сходящихся сил на координатные оси равна алгебраическим суммам проекций этих сил на соответствующие оси: Rx=åFix; Ry=åFiy; Rz=åFiz; Условия равновесия сист. сходящихся сил: геометрическое:
Проекция силы на ось – алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси. Проекция вектора суммы на какую-нибудь ось равна алгебраической проекций слагаемых векторов на ту же ось.
Система двух параллельных сил, равных по модулю и направленных в разные стороны, назыв. парой сил. Кратчайшее расстояние между линиями действия этих сил назыв. плечом пары "h". Действия пары сил характеризуется ее моментом. Момент пары сил M = F×h – произведение модуля одной из сил пары на ее плечо. Момент пары сил
Момент силы относительно точки – вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся повернуться против хода час.стрелки. Плечо "h"– кратчайшее расстояние от точки до линии действия силы.
Главный вектор – векторная сумма всех сил, приложенных к телу. Главный момент относительно центра –векторная сумма моментов всех сил, приложенных к телу относительно того же центра. Теорема (лемма) о параллельном переносе силы: сила приложенная в какой-либо точке тверд. тела, эквивалента такой же силе, приложенной в любой др. точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Основная теорема статики. Любую систему сил можно свести к 2м векторам, к главному вектору всех сил F0 и к главному моменту М0 всех сил. Оба вектора можно разложить на составляющие.
Чистый сдвиг
При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг, g» δ/а — относительный сдвиг или угол сдвига. Закон Гука при сдвиге:γ=τ/G или τ=Gγ. G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге.G=E/2(1+µ) (Е — модуль упругости, m— коэффициент Пуассона).
Потенциальная энергия при сдвиге: U=δQ/V=Q2a/2GF. Удельная потенциальная энергия деформации при сдвиге: u=U/V=Q2a/2GFaF,где V=а×F — объем элемента. Учитывая закон Гука, u=τ2/2G. Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю. напряженность τ=P/ℓδ τ =Mвн/2πR2δ σα= τ ABsinα+ τ BCcosα σ τ α= τ ABcosα- τ BCsinα AB=AC cos α, BC=AC sin α. Отсюда следует, что: σα= τ sin2α τ α= τ cos2α
15. Центртяжести твердого тела – точка, неизменно связанная с этим телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела при любом положении тела в пространстве. При этом поле тяжести считается однородным, т.е. силы тяжести частиц тела параллельны друг другу и сохраняют постоянную величину при любых поворотах тела. Координаты центра тяжести:
Статический момент площади плоской фигуры – сумма произведений элементарных площадей, входящих в состав площади фигуры, на алгебраические значения расстояний до некоторой оси. Sx=åyi×DFi= F×yc; Sy=åxi×DFi= F×xc. Вспомогательные теоремы для определения положения центра тяжести: Т.1. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Т.2. Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости. Т.3. Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести, V=2pxcF.
Определяя положение центра тяжести плоской фигуры с вырезанной из нее частью, можно считать площадь этой части отрицательной и тогда:
24.Теорема о сложении скоростей:
25.Теорема о сложении ускорений (теорема Кориолиса):
3) 4) получаем:
23.Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки А откладываем под углом 20.Движение твердого тела. При сложении двух поступательных движений результирующее движение также является поступательным и скорость результирующего движения равна сумме скоростей составляющих движений. Сложение вращений тв. тела вокруг пересекающихся осей. Ось вращения, положение которой в пространстве изменяется со временем назыв. мгновенной осью вращения тела. Вектор угловой скорости – скользящий вектор, направленный вдоль мгновенной оси вращения. Абсолютная угловая скорость тела = геометрической сумме скоростей составляющих вращений – правило параллелограмма угловых скоростей.
27.Теорема об изменении количества движения матер. точки.
28. Теорема об изменении момента количества движения матер. точки.
29.Работа силы. Мощность. Элементарная работа dA = Ftds, Ft – проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscosa. Если a – острый, то dA>0, тупой – <0, a=90o: dA=0. dA=
Теорема о работе силы: Работа равнодействующей силы равна алгебраической сумме работ составляющих сил на том же перемещении А=А1+А2+…+Аn. Работа силы тяжести: Работа силы упругости: Работа силы трения: если сила трения const, то Работа силы тяготения. Сила притяжения (тяготения): Мощность – величина, определяющая работу в единицу времени, = 1000 Вт, 1л.с.(лошадиная сила) = 75 кгс×м/с = 736 Вт].
30.Теорема об изменении кинетической энергии точки. В диффер-ной форме: Силовое поле – область, в каждой точке которой на помещенную в ней матер.точку действует сила, однозначно определенная по величине и направлению в любой момент времени, т.е. должно быть известна 1) Работа сил стац. поля зависит в общем случае от начального М1 и конечного М2 положений и траектории, но не зависит от закона движения матер. точки. 2) Имеет место равенство А2,1= – А1,2. Для нестационарных полей эти свойства на выполняются. Примеры: поле силы тяжести, электростатическое поле, поле силы упругости. Стационарные силовые поля, работа сил которых не зависит от траектории (пути) движения матер. точки и определяется только ее начальным и конечным положениями назыв. потенциальными (консервативными).
Моменты инерции сечения
Полярный момент инерции сечения относительно некоторой точки (полюса) — сумма произведений элементарных площадок на квадраты их расстояний от этой точки. Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: Jmax + Jmin= Jx + Jy. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям: Jx1=Jmaxcos2a + Jminsin2a; Jy1=Jmaxcos2a + Jminsin2a; Jx1y1= Конечной целью вычисления геометрических характеристик сечения является определение главных центральных моментов инерции и положения главных центральных осей инерции. Радиус инерции —
Интеграл Мора Универсальный метод определения перемещений (линейных и углов поворота) – метод Мора. К системе прикладывают единичную обобщенную силу в точке, для которой ищется обобщенное перемещение. Если определяется прогиб, то единичная сила представляет собой безразмерную сосредоточенную силу, если определяется угол поворота, то – безразмерный единичный момент. В случае пространственной системы действуют шесть компонентов внутренних усилий. Обобщенное перемещение определяется Сила. Система сил. Равновесие тела. Равновесие – состояние покоя по отношению к другим телам, например к Земле. Равновесие жидких и газообразных тел рассматривается в курсах гидростатики и аэростатики. Прямая, по которой направлена сила, назыв. линией действия силы. Система сил – совокупность сил, действующих на рассматриваемое тело. Если линии действия всех сил лежат в одной плоскости, система сил называется плоской, а если линии действия сил лежат не в одной плоскости, - пространственной. Существуют сходящиеся и параллельные линии действия сил. Тело, которому из данного положения можно сообщить любое перемещение в пространстве – свободное. Если заменить систему сил другой, при этом не изменяя состояние покоя или движения, - эквивалентная система сил. Если под действием сил тело находится в покое, то система сил называется уравновешенной или эквивалентной 0. Если система сил = одной силе, то она равнодействующая. Имеющая противоположное направление – уравновешивающая. Внешние силы – силы со стороны других тел, внутренние – силы, с которыми части данного тела действуют друг на друга. Сила, приложенная к одной точке – сосредоточенная. Уравновешенные силы: Система сил, под действием которой свободное твердое тело может находится в покое, называется уравновешенной.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.61.142 (0.066 с.) |
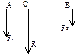 Сила – мера механического взаимодействия тел. Сила векторная величина, характеризуется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Ед.измерения – ньютон,
Сила – мера механического взаимодействия тел. Сила векторная величина, характеризуется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Ед.измерения – ньютон,  , 1кН (килоньютон)= 103Н.
, 1кН (килоньютон)= 103Н.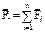 . Равнодействующая может быть найдена геометрич. способом – построением силового (векторного) многоугольника или аналитич. способом, проектируя силы на оси координат. Проекции силы на оси координат (для плоской сист.): Fx=F×cosa; Fy=F×cosb=F×sina; проекция >0, если направление составляющей силы совпадает с направл. оси. Модуль силы:
. Равнодействующая может быть найдена геометрич. способом – построением силового (векторного) многоугольника или аналитич. способом, проектируя силы на оси координат. Проекции силы на оси координат (для плоской сист.): Fx=F×cosa; Fy=F×cosb=F×sina; проекция >0, если направление составляющей силы совпадает с направл. оси. Модуль силы: 
 ; направляющие косинусы:
; направляющие косинусы: 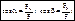 разложение силы на составляющие:
разложение силы на составляющие:  , где
, где  – орт (единичный вектор) соответствующей оси.
– орт (единичный вектор) соответствующей оси.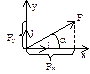 Для пространственной системы:
Для пространственной системы:  ,
, Fx=Fcosa; Fy=Fcosb; Fz=Fcosg;
Fx=Fcosa; Fy=Fcosb; Fz=Fcosg; 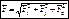 ;
; 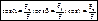 .
. .
.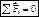
 аналитические: åFix=0; åFiy=0; åFiz=0. Теорема о трех непараллельных силах: Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
аналитические: åFix=0; åFiy=0; åFiz=0. Теорема о трех непараллельных силах: Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.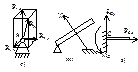 5. Сложение параллельных сил.
5. Сложение параллельных сил.
 Теория пар сил. Сложение двух параллельных сил: равнодейст-ющая двух парал-ых сил F1 и F2 одного направления имеет такое же направление, ее модуль равен сумме модулей слагаемых сил, а точка приложения делит отрезок между точками приложения сил на части обратно пропорциональные модулям сил: R=F1 + F2; АС/ВС=F2/F1. Равнодействующая двух противоположно направленных паралл-ных сил имеет направление силы большей по модулю и модуль, равный разности модулей сил.
Теория пар сил. Сложение двух параллельных сил: равнодейст-ющая двух парал-ых сил F1 и F2 одного направления имеет такое же направление, ее модуль равен сумме модулей слагаемых сил, а точка приложения делит отрезок между точками приложения сил на части обратно пропорциональные модулям сил: R=F1 + F2; АС/ВС=F2/F1. Равнодействующая двух противоположно направленных паралл-ных сил имеет направление силы большей по модулю и модуль, равный разности модулей сил. – вектор, направленный перпендикулярно плоскости сил, так, что, если смотреть ему навстречу, то видим вращение пары против хода час.стр. M>0, если против час.стр., M<0 – по час.стр (на рис М>0).
– вектор, направленный перпендикулярно плоскости сил, так, что, если смотреть ему навстречу, то видим вращение пары против хода час.стр. M>0, если против час.стр., M<0 – по час.стр (на рис М>0).
 Теоремы о парах. 1) Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар.
Теоремы о парах. 1) Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. 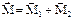 . 2) Две пары, имеющие геометрически равные моменты, эквиваленты. 3) Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее действия. Т.е. момент пары сил является свободным вектором. 4) Система нескольких пар сил эквивалента одной паре, момент которой равен векторной сумме моментов данных пар. Т.е. система пар приводится к одной паре, момент которой равен сумме моментов всех пар. Условие равновесия пар сил:
. 2) Две пары, имеющие геометрически равные моменты, эквиваленты. 3) Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее действия. Т.е. момент пары сил является свободным вектором. 4) Система нескольких пар сил эквивалента одной паре, момент которой равен векторной сумме моментов данных пар. Т.е. система пар приводится к одной паре, момент которой равен сумме моментов всех пар. Условие равновесия пар сил:  – геометрическая сумма их моментов равна 0. Пары сил, расположенные в одной плоскости, взаимно уравновеш-тся, если алгебраическая сумма их моментов åМi=0.
– геометрическая сумма их моментов равна 0. Пары сил, расположенные в одной плоскости, взаимно уравновеш-тся, если алгебраическая сумма их моментов åМi=0.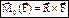 – момент силы равен векторному произведению вектора
– момент силы равен векторному произведению вектора 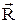 на вектор
на вектор  . Модуль векторного произведения:
. Модуль векторного произведения:  R×F×sina= F×h. Для плоской сист. сил обычно находят не вектор момента, а только его модуль:
R×F×sina= F×h. Для плоской сист. сил обычно находят не вектор момента, а только его модуль:  ±F×h, >0 – против час.стр.; <0 – по час.стр. Свойства момента силы: 1) момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия; 2) момент силы относит. точки =0 только тогда, когда сила =0 или когда линия действия силы проходит через точку (т.е. плечо =0). Если x,y,z – координаты точки приложения силы, Fx, Fy, Fz – проекции силы на оси координат и точка 0 – начало координат, то
±F×h, >0 – против час.стр.; <0 – по час.стр. Свойства момента силы: 1) момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия; 2) момент силы относит. точки =0 только тогда, когда сила =0 или когда линия действия силы проходит через точку (т.е. плечо =0). Если x,y,z – координаты точки приложения силы, Fx, Fy, Fz – проекции силы на оси координат и точка 0 – начало координат, то =(yFz – zFy)
=(yFz – zFy)  +(zFx – xFz)
+(zFx – xFz)  +(xFy – yFx)
+(xFy – yFx)  , откуда проекции момента силы на оси коорд.: М0x(
, откуда проекции момента силы на оси коорд.: М0x(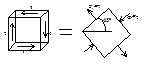 Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения τ=Q/F, где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: σ1=-σ3 σ2=0 Главные площадки составляют с площадками чистого сдвига угол 45о.
Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения τ=Q/F, где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: σ1=-σ3 σ2=0 Главные площадки составляют с площадками чистого сдвига угол 45о. ;
; 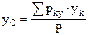 ;
;  , где Р=åрk, xk,yk,zk – координаты точек приложения сил тяжести рk. Центр тяжести – геометрическая точка и может лежать и вне пределов тела (например, кольцо). Центр тяжести плоской фигуры:
, где Р=åрk, xk,yk,zk – координаты точек приложения сил тяжести рk. Центр тяжести – геометрическая точка и может лежать и вне пределов тела (например, кольцо). Центр тяжести плоской фигуры:
 , DFk – элементарная площадка, F – площадь фигуры. Если площадь нельзя разбить на несколько конечных частей, то
, DFk – элементарная площадка, F – площадь фигуры. Если площадь нельзя разбить на несколько конечных частей, то 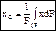 . Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Центр тяжести: дуги окружности с центральным углом 2a:
. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Центр тяжести: дуги окружности с центральным углом 2a: 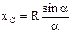 ; кругового сектора:
; кругового сектора: 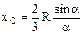 ; треугольник: в точке пересеч. медиан (1/3 медианы от основания).
; треугольник: в точке пересеч. медиан (1/3 медианы от основания). Т.4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести, F=2pxcL.
Т.4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести, F=2pxcL.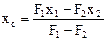 и т.д. — способ отрицательных площадей (объемов).
и т.д. — способ отрицательных площадей (объемов).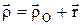 ,
, 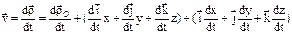 ; рчастныепоэтому скорость его конца
; рчастныепоэтому скорость его конца  и т.д., Þ:
и т.д., Þ:  ,
, ;
;  – относительная скорость.
– относительная скорость. ; переносная скорость:
; переносная скорость:  , поэтому абсолютная скорость точки = геометрической сумме ее переносной (ve) и относительной (vr) скоростей
, поэтому абсолютная скорость точки = геометрической сумме ее переносной (ve) и относительной (vr) скоростей  , модуль:
, модуль:  .
.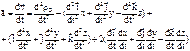
 и т.д. Слагаемые выражения, определяющего ускорения
и т.д. Слагаемые выражения, определяющего ускорения  : 1)
: 1) 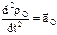 – ускорение полюса О;
– ускорение полюса О;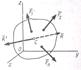
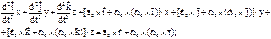
 – относительное ускорение точки;
– относительное ускорение точки;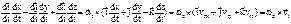 ,
,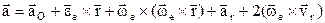 .
.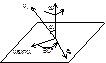 Первые три слагаемых представляют собой ускорение точки в переносном движении:
Первые три слагаемых представляют собой ускорение точки в переносном движении: 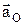 – ускорение полюса О;
– ускорение полюса О;  – вращательное уск.,
– вращательное уск.,  – осестремительное уск., т.е.
– осестремительное уск., т.е. 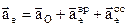 .
.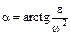 к ускорению аА отрезок
к ускорению аА отрезок  , при этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол
, при этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол  :
: 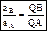 . Мгновенный центр скоростей Р и мгновенный центр ускорений Q являются различными точками плоской фигуры.
. Мгновенный центр скоростей Р и мгновенный центр ускорений Q являются различными точками плоской фигуры.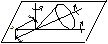
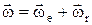 . Если тело участвует одновременно в мгновенных вращениях вокруг нескольких осей, пересекающихся в одной точке, то
. Если тело участвует одновременно в мгновенных вращениях вокруг нескольких осей, пересекающихся в одной точке, то
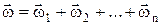 . При сферическом движении твердого тела, одна из точек которого во все время движения остается неподвижной, имеем уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Угловая скорость прецессии
. При сферическом движении твердого тела, одна из точек которого во все время движения остается неподвижной, имеем уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Угловая скорость прецессии 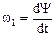 , угл. скорость нутации
, угл. скорость нутации 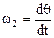 , угл. ск. собственного вращения
, угл. ск. собственного вращения 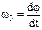 .
.  ,
, – модуль угловой скорости тела вокруг мгновенной оси. Через проекции на неподвижные оси координат:
– модуль угловой скорости тела вокруг мгновенной оси. Через проекции на неподвижные оси координат: 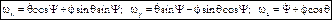 – кинематические уравнения Эйлера.
– кинематические уравнения Эйлера.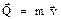 – количество движения материальной точки,
– количество движения материальной точки,  – элементарный импульс силы.
– элементарный импульс силы. 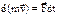 – элементарное изменение количества движения материальной точки равно элементарному импульсу силы, приложенной к этой точке (теорема в дифференц-ной форме) или
– элементарное изменение количества движения материальной точки равно элементарному импульсу силы, приложенной к этой точке (теорема в дифференц-ной форме) или  – производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке. Проинтегрируем:
– производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке. Проинтегрируем:  – изменение количества движения материальной точки за конечный промежуток времени равно элементарному импульсу силы, приложенной к этой точке, за тот же промежуток времени.
– изменение количества движения материальной точки за конечный промежуток времени равно элементарному импульсу силы, приложенной к этой точке, за тот же промежуток времени. 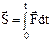 – импульс силы за промежуток времени [0,t]. В проекциях на оси координат:
– импульс силы за промежуток времени [0,t]. В проекциях на оси координат: 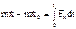 и т.д.
и т.д.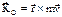 - момент количества движения матер. точки относительно центра О.
- момент количества движения матер. точки относительно центра О. 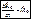 – производная по времени от момента количества движения матер. точки относительно какого-либо центра равна моменту силы, приложенной к точке, относительно того же центра. Проектируя векторное равенство на оси координат. получаем три скалярных уравнения:
– производная по времени от момента количества движения матер. точки относительно какого-либо центра равна моменту силы, приложенной к точке, относительно того же центра. Проектируя векторное равенство на оси координат. получаем три скалярных уравнения: 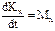 и т.д. - производная от момента кол-ва движения матер. точки относительно какой-либо оси равна моменту силы, приложенной к точке, относительно той же оси. При действии центральной силы, проходящей через О, МО= 0, Þ
и т.д. - производная от момента кол-ва движения матер. точки относительно какой-либо оси равна моменту силы, приложенной к точке, относительно той же оси. При действии центральной силы, проходящей через О, МО= 0, Þ  =const.
=const.  =const, где
=const, где 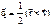 – секторная скорость. Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью, т.е. радиус-вектор точки описывает ("ометает") равные площади в любые равные промежутки времени (закон площадей) Этот закон имеет место при движении планет и спутников – один из законов Кеплера.
– секторная скорость. Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью, т.е. радиус-вектор точки описывает ("ометает") равные площади в любые равные промежутки времени (закон площадей) Этот закон имеет место при движении планет и спутников – один из законов Кеплера. – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= Fxdx+Fydy+Fzdz – аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М0М1:
– скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= Fxdx+Fydy+Fzdz – аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М0М1: 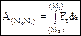 . Если сила постоянна, то
. Если сила постоянна, то  = F×s×cosa. Единицы работы:[1 Дж (джоуль) = 1 Нм].
= F×s×cosa. Единицы работы:[1 Дж (джоуль) = 1 Нм].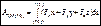 , т.к. dx=
, т.к. dx=  dt и т.д., то
dt и т.д., то 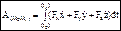 .
. , >0, если начальная точка выше конечной.
, >0, если начальная точка выше конечной.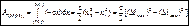 –работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.
–работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.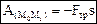 - всегда отрицательна, Fтр=fN, f – коэфф.трения, N – нормальная реакция поверхности.
- всегда отрицательна, Fтр=fN, f – коэфф.трения, N – нормальная реакция поверхности.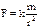 , из mg=
, из mg= 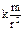 , находим коэфф. k=gR2.
, находим коэфф. k=gR2. 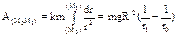 – не зависит от траектории.
– не зависит от траектории.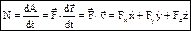 . Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) =
. Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) =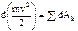 – полный дифференциал кинетической энергии мат.точки = элементарной работе всех действующих на точку сил.
– полный дифференциал кинетической энергии мат.точки = элементарной работе всех действующих на точку сил.  – кинетическая энергия матер.точки. В конечном виде:
– кинетическая энергия матер.точки. В конечном виде: 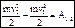 – изменение кинетической энергии мат.точки, при переходе ее из начального в конечное (текущее) положение равно сумме работ на этом перемещении всех сил, приложенных к точке.
– изменение кинетической энергии мат.точки, при переходе ее из начального в конечное (текущее) положение равно сумме работ на этом перемещении всех сил, приложенных к точке.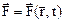 . Нестационарное силовое поле, если
. Нестационарное силовое поле, если  и Fx=Fx(x,y,z) и т.д. Свойства стационар. силовых полей:
и Fx=Fx(x,y,z) и т.д. Свойства стационар. силовых полей: , где I и II – любые пути, А1,2 – общее значение работы. В потенциальных силовых полях существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так:
, где I и II – любые пути, А1,2 – общее значение работы. В потенциальных силовых полях существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так: . Функция U=U(x1,y1,z1,x2,y2,z2,…xn,yn,zn) назыв. силовой функцией. Элементарная работа сил поля: dА=ådАi= dU. Если силовое поле является потенц-ным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции. Работа сил на конечном перемещении
. Функция U=U(x1,y1,z1,x2,y2,z2,…xn,yn,zn) назыв. силовой функцией. Элементарная работа сил поля: dА=ådАi= dU. Если силовое поле является потенц-ным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции. Работа сил на конечном перемещении 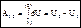 , т.е. работа сил в потенц-ном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергия П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П0= 0. П=П(x1,y1,z1,x2,y2,z2,…xn,yn,zn). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А1,2= П1– П2. Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U0: А1,0= П =U0 – U. Потенциальная энергия поля силы тяжести: П= mgz. Потенц.энерг.поля центральных сил. Центральная сила – сила, которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра:
, т.е. работа сил в потенц-ном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергия П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П0= 0. П=П(x1,y1,z1,x2,y2,z2,…xn,yn,zn). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А1,2= П1– П2. Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U0: А1,0= П =U0 – U. Потенциальная энергия поля силы тяжести: П= mgz. Потенц.энерг.поля центральных сил. Центральная сила – сила, которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра: 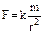 ,
,  . Центральной является гравитационная сила
. Центральной является гравитационная сила 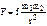 ,
,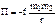 , f = 6,67×10-11м3/(кгс2) – постоянная тяготения. Первая космическая скорость v1=
, f = 6,67×10-11м3/(кгс2) – постоянная тяготения. Первая космическая скорость v1=  » 7,9 км/с, R = 6,37×106м – радиус Земли; тело выходит на круговую орбиту. Вторая космическая скорость: v11=
» 7,9 км/с, R = 6,37×106м – радиус Земли; тело выходит на круговую орбиту. Вторая космическая скорость: v11=  » 11,2 км/с, траектория тела парабола, при v >v11– гипербола. Потенц. энергия восстанавливающей силы пружин:
» 11,2 км/с, траектория тела парабола, при v >v11– гипербола. Потенц. энергия восстанавливающей силы пружин: , l – модуль приращения длины пружины. Работа восстанавливающей силы пружины:
, l – модуль приращения длины пружины. Работа восстанавливающей силы пружины:  , l1 и l2 – деформации, соответствующие начальной и конечной точкам пути.
, l1 и l2 – деформации, соответствующие начальной и конечной точкам пути.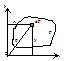 Осевой (экваториальный) момент инерции сечения — сумма произведений элементарных площадок dF на квадраты их расстояний до оси.
Осевой (экваториальный) момент инерции сечения — сумма произведений элементарных площадок dF на квадраты их расстояний до оси.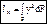 ;
;  [см4, м4, т.д.].
[см4, м4, т.д.]. ; [см4, м4, т.д.]. Jy + Jx = Jp.
; [см4, м4, т.д.]. Jy + Jx = Jp. , если a0>0 Þ оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:
, если a0>0 Þ оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей: 
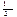 (Jmax — Jmin)sin2a;
(Jmax — Jmin)sin2a;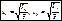 ; Jx=F×ix2, Jy=F×iy2.
; Jx=F×ix2, Jy=F×iy2. Если Jx и Jy главные моменты инерции, то ix и iy — главные радиусы инерции. Эллипс, построенный на главных радиусах инерции как на полуосях, называется эллипсом инерции. При помощи эллипса инерции можно графически найти радиус инерции ix1 для любой оси х1. Для этого надо провести касательную к эллипсу, параллельную оси х1, и измерить расстояние от этой оси до касательной. Зная радиус инерции, можно найти момент инерции сечения относительно оси х1:
Если Jx и Jy главные моменты инерции, то ix и iy — главные радиусы инерции. Эллипс, построенный на главных радиусах инерции как на полуосях, называется эллипсом инерции. При помощи эллипса инерции можно графически найти радиус инерции ix1 для любой оси х1. Для этого надо провести касательную к эллипсу, параллельную оси х1, и измерить расстояние от этой оси до касательной. Зная радиус инерции, можно найти момент инерции сечения относительно оси х1: 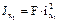 . Для сечений, имеющих более двух осей симметрии (например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех центральных осей равны между собой, Jxy=0, эллипс инерции обращается в круг инерции.
. Для сечений, имеющих более двух осей симметрии (например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех центральных осей равны между собой, Jxy=0, эллипс инерции обращается в круг инерции.


