Объединительная классификация

Любое суждение имеет и количественную, и качественную характеристики. Поэтому в логике применяется объединенная классификация суждений по количеству и качеству.

1. Общеутвердительное суждение - общее по объему субъекта и утвердительное по качеству связки. Его структура: «Все S есть Р». Символом служит латинская буква «А», первая гласная слова УТВЕРЖДАЮ – Affirmo.

Объем Р шире объема S и является подчиняющим понятием.

Р

Объемные отношения субъекта и предиката в таких суждениях можно изобразить в виде указанной круговой схемы.

S

S, Р

 

 

Пример: «Всякое определение является суждением».

Во многих «А» (во всех определениях) Sи Р - равнозначные понятия – и объемы терминов полностью совпадают.

Пример: «Все равносторонние прямоугольники – квадраты».

2. Частноутвердительное суждение - частное по объему субъекта и утвердительное по качеству связки. Его структура: «Некоторые S есть Р». Символом служит латинская буква «I» вторая гласная слова УТВЕРЖДАЮ – Affirmo.

Р

S

В этих суждениях Sи Р- перекрещивающиеся понятия, их объемы, частично совпадают.

Пример: «Некоторые суждения – истинные».

В некоторых «I» объем S шире объема Р, и Р - является подчиняющим понятием.

Пример: « Среди животных есть хищники».

Р

S

3. Общеотрицательное суждение - общее по объему субъекта и отрицательное по качеству связки. Его структура: «Ни одно S не есть Р». Символом служит латинская буква «Е» - первая гласная слова ОТРИЦАЮ – Nego.

 

Характерна полная несовместимость Sи Р, т.е. их объемы полностью исключают друг друга.

Пример: «Киты не дышат жабрами».

4. Частноотрицательное суждение - частное по объему субъекта и отрицательное по качеству связки. Его структура: «Некоторые S не есть Р». Символом служит латинская буква «О» - вторая гласная слова ОТРИЦАЮ – Nego.

Пример: «Некоторые грибы не являются ядовитыми».

Пример: «Некоторые цветы не являются гвоздиками».

Объемные отношения Sи Р напоминают аналогичные схемы в частноутвердительных суждениях с той лишь разницей, что в утвердительных - речь идет о совпадающей части объемов терминов, а в отрицательных - о несовпадающей части.

S

Р

S

Р

 

 

Распределенность терминов в атрибутивном суждении

Получение достоверных выводов и построение убедительных доказательств, зависит от правильности

оперирования в рассуждениях различными видами суждений, что предполагает знание распределенности терминов - соотношения их объемов. Термин считается распределенным, (развернутым, взятым в полном объеме)если он полностью входит в объем другого термина или же полностью из него исключается. Распределённый термин обозначается знаком «+». В случае частичного совпадения объемов терминов они считаются нераспределенными (неразвернутыми, неисчерпанными). Нераспределённый термин обозначается знаком «-».

Субъекты распределены в общих суждениях и не распределены в частных. Предикаты распределены в отрицательных суждениях и не распределены в утвердительных.

Отношения между простыми суждениями

Человек сталкивается с различными мнениями, суждениями, для верного анализа - необходимо иметь четкое представление о тех отношениях, в которых они могут находиться между собой. Выделяют отношения: сравнимые, имеющие одинаковые термины и различающиеся по качеству или количеству (делятся на совместимые и несовместимые), и несравнимые, имеющие различные субъекты или предикаты.

Пример: «Земля - планета» и «Адвокаты - юристы».

Эти суждения не соотносятся не по истинности не по ложности.

Совместимые суждения - различают три вида.

1.Равнозначащие (эквивалентность) суждения, выражающие одну и ту же мысль, но их логическое построение различно.

Пример: «Ю. Гагарин – первый в мире космонавт» и «Первый человек, полетевший в космос».

Если истинно одно, то истинно и другое.

2.Частичная совместимость (субконтрарность) характерна для «I» и «О» суждений.

Пример: «Некоторые юристы - адвокаты» (истинное) и «Некоторые адвокаты – не юристы» (ложное).

Могут быть одновременно истинными, но не могут быть одновременно ложными.

3.Отношения подчинения характерны для суждений, которые одинаковы по качеству и различны по количеству.

Пример: «Большинство из нашей группы учатся хорошо» и «Все студенты нашей группы хорошо учатся».

В данном случае подчиняющим являются «А» и «Е», а подчиненным «I» и «О». При истинности подчиняющего - подчиненное всегда будет истинным.

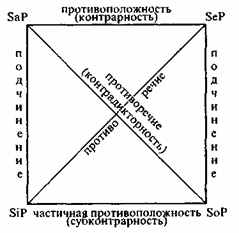
Несовместимые суждения – не могут быть одновременно истинными.

1.Противоположные (контрарность) - общие суждения, выражающие противоположные мысли.

Пример: «Все деревья - хвойные» и «Ни одно дерево – не хвойное».

Не могут быть одновременно истинными, но могут быть одновременно ложными. Истинность одного из противоположных суждений определяет ложность другого.

2.Противоречащие (контрадикторность) - суждения, которые взаимно исключают друг друга.

Пример: «Все обитатели моря - рыбы» и

«Некоторые обитатели моря - никакие не рыбы».

Не могут быть одновременно ни истинными, ни ложными. При истинности одного - другое ложно и наоборот.

Отношения между простыми суждениями рассматриваются с помощью схемы, называемой логическим квадратом.

Его вершины - простые категорические суждения - А, Е, I, О;а стороны и диагонали - отношения между суждениями.

СЛОЖНЫЕ СУЖДЕНИЯ

Сложные суждения образуются из простых путем их соединения. Структурообразующими элементами выступают не понятия-термины, а самостоятельные суждения. Связь между ними осуществляется не с помощью связки «есть» («не есть»), а посредством логических союзов (логических связок).

Они могут бытьистинными или ложными, что зависит, от истинности или ложности составляющих их простых и иных суждений.

1.Конъюнктивные (соединительные) «L» - суждения, объединяемые связками «и», «но», «да», «а», «а так же», «хотя», «однако». Р L q

Пример: «Ночи бывают лунные и безлунные».

Состоит из суждений: «Ночи бывают лунные» и «Ночи бывают безлунные». Суждение истинно тогда и только тогда, когда истинны всесоставляющие его простые суждения.

2.Дизъюнктивные (разделительные ) - суждения, включающее в качестве составных частей суждения-дизъюнкты.

Две разновидности:

Слабая (нестрогая) «V» образуется логическими союзами «или», «либо». Объединяемые суждения не исключают друг друга. Р V q

Пример: «Солнце светит или дождь».

Суждение истинно в тех случаях, когда истинно, хотя бы одно из составляющих ее суждений, и ложно, когда оба - ложны.

Сильная (строгая) «V» образуется логическими союзами «либо...либо», «или...или», «то… то». Составляющие ее суждения исключают друг друга. Р V q

Пример: «Будет либо дождь, либо снег».

Суждение истинно лишь тогда, когда одно из составляющих ее суждений истинно, а другое ложно.

3.Импликативные (условные) «→» - суждения, включающее в качестве составных два суждения - основание и следствие, объединяемые связками «если..., то...», «тем..., где...», «тогда..., когда...», «поскольку..., постольку...», «в случае если…то…». P → q

Пример: «Если Мария - жена, то она замужем».

Суждение ложно тогда и только тогда, когда основание истинно, а следствие ложно.

4. Эквивалентные (двойная импликация) «↔» - суждения, связанные двойной условной зависимостью, выражаемые связками «если и только если..., то...», «тогда и только тогда…, когда…», «лишь в том случае, если…то…».

P ↔ q

Пример: «Если и только если вы медленно потянете полоску за свешивающийся край в направлении от стола, то стакан двинется вместе с полоской».

Суждение истинно тогда и только тогда, когда составляющие его простые суждения либо одновременно истинны, либо одновременно ложны.

5. Отрицание «┐» -суждение выраженное словами «неверно что…», «неправда, что…», «не».

Пример: «Все судьи неподкупны». «Неверно, что все судьи неподкупны». Или «Не все судьи не подкупны».

Исходное суждение истинно, двойное ложно.

Таблица 2.1.

р	┐р	┐ ┐р
И Л	Л И	И Л

Истинность и ложность сложных суждений отразим в таблице истинности 2.2.

Р	g	P L g	P V g	P V g	P → g	P ↔ g
И	И	И	И	Л	И	И
И	Л	Л	И	И	Л	Л
Л	И	Л	И	И	И	Л
Л	Л	Л	Л	Л	И	И

Логические операции с суждениями

Преобразование простых атрибутивных суждений

Для раскрытия всей гаммы содержания суждения используют операции преобразования.

I. Обращение (конверсия) – это преобразование путём перестановки его S и Р. По количеству суждение может изменяться, а по качеству – всегда постоянно.

«S есть Р» → «Р есть S»

ЗАКОНОМЕРНОСТИ:

1. А→I, обусловлено тем, что S – распределён, а Р – нераспределён (обращение с ограничением).

Формула обращения:

«Все S есть Р» → «Некоторые Р есть S»

Пример: «Все россияне имеют право на социальную защиту» → «Некоторые имеющие право на социальную защиту – россияне».

2. А→А, чистое обращение. S и Р – распределёны.

Формула чистого обращения:

«Все S есть Р» → «Все Р есть S»

Пример: «Равносторонний треугольник - это треугольник, у которого все стороны равны». «Треугольник, у которого все стороны равны - это равносторонний треугольник

3. I→I, - обусловлено тем, что S и Р – нераспределёны.

Формула обращения:

«Некоторые S есть Р» → «Некоторые Р есть S»

Пример: «Некоторые студенты - спортсмены» → «Некоторые спортсмены - студенты».

4. I→А, обусловлено тем, что S – распределён, а Р – нераспределен.

Формула обращения:

«Некоторые S есть Р» → «Все Р есть S»

Пример: «Некоторые преступники - убийцы» → «Все убийцы - преступники».

5. Е→Е, обусловлено тем, что S и Р – распределёны.

Формула обращения:

«Ни одно S не есть Р» → «Ни одно Р не есть S»

Пример: «Ни один идеалист не является материалистом» → «Ни один материалист не является идеалистом».

6. Частноотрицательные «О» – не обращаются,т.к. S – нераспределён, а следовательно он не может стать Р нового отрицательного суждения, где он – распределён.

 

Пример: «Некоторые ученные – не академики» → «Ни один академик – не ученный».

«Некоторые мужчины – не женаты» → «Ни один женатый – не мужчина».

Эти выводы – бессмысленные.

II. Превращение ( обверсия ) - это преобразование путём изменения его качества на противоположное - Р→не-Р. Характерно двойное отрицание – что бы смысл ни менялся. Количество - постоянно, а S и Р при этом не меняются местами.

«S есть Р» → «S не есть не-Р»

ЗАКОНОМЕРНОСТИ:

1. А → Е.

Формула превращения:

«Все S есть Р» → «Ни одно S не есть не-Р»

Пример: «Все студенты нашей группы являются успевающими» → «Ни один студент нашей группы не является не успевающим».

2. Е → А.

Формула превращения:

«Ни одно S не есть не-Р» → «Все S есть Р»

Пример: «Ни одно преступление не остаётся не раскрытым» → «Все преступления раскрываются».

3. I → О.

Формула превращения:

«Некоторые S есть Р» → «Некоторые S не есть не-Р»

Пример: «Многие люди получают пенсию» → «Некоторые люди не получает не пенсии».

4. О → I.

Формула превращения:

«Некоторые S не есть Р» → «Некоторые S есть не-Р»

Пример: «Некоторые животные не являются кошками» → «Некоторые животные являются не кошками».

III. Противопоставление субъекту - это преобразование вначале путём обращения (качество не меняется, а количество Р и S - меняются), а затем путём превращения (качество меняется на противоположное).

Пример: 1. Обратим - А → I:

«Все S есть Р» → «Некоторые Р есть S».

«Все адвокаты юристы» → «Некоторые юристы – адвокаты».

2. Превратим - I → О:

«Некоторые Р есть S» → «Некоторые Р не есть не-S».

«Некоторые юристы – адвокаты» → «Некоторые юристы не есть не адвокаты».

IV. Противопоставление предикату - это преобразование вначале путём превращения, а затем путём обращения.

Пример: 1. Превратим – А → Е:

«Все S есть Р» → «Ни одно S не есть не-Р».

«Все адвокаты юристы» → «Ни один адвокат не является не юристом».

2. Обратим - Е → Е:

«Ни одно S не есть не-Р»→«Ни одно не-Р не есть S».

«Ни один адвокат не является не юристом». → «Ни один не юрист не является адвокатом».

Значение преобразований:

1. раскрывает, новый более богатый смысл;

2. позволяет извлечь дополнительную информацию.

Ограничение простых атрибутивных суждений

Ограничение - это логическая операция, при которой S и Р ограничиваются путем прибавления одного и того же признака по схеме:

S есть Р → aS есть аР

Пример: «Все кошки - хищники» → «Все домашние кошки - домашние хищники».

Как правило, ограничения в целом неправомерны, не всегда суждения, полученные с помощью прибавление признаков, являются состоятельными.

Пример: «Черепаха – животное» → «Быстрая черепаха - быстрое животное» - это не так, но если «Все черепахи – животные», то «Все морские черепахи - морские животные».

Почему в одном случае суждение правомерно, а в другом случае - нет? Логика ставит условия, при выполнении которых суждения являются правомерными. В качестве такого правила для общеутвердительных суждений (А) может быть сформулировано следующее: ограничивающий признак не может иметь никаких количественных градаций, т. е. этот признак должен быть точечным свойством. Этим свойством предмет может или обладать, или не обладать, но не может обладать в какой-то степени. В примерах «хищник», «домашний», «морской» представляют собой точечные свойства. Свойство «быстрый» - не точечное, а линейное. Такие свойства не должны выступать в качестве ограничивающих признаков.

В суждениях общеутвердительных, S - распределен, Р - нераспределен. Если же S и Р, тождественны по объему, или же суждения общеотрицательные, когда S и Р распределены, то операция ограничения всегда правомерна, независимо от характера ограничивающего признака.

Пример: «Квадраты являются равносторонними прямоугольниками» → «Значит, большие квадраты являются большими равносторонними прямоугольниками».

Вывод: ограничение простых атрибутивных суждений будут правомерны в том случае, когда S и Р - распределены.

Отрицание суждения - это операция, состоящая в преобразовании логического содержания отрицаемого суждения, конечным результатом которой является формулирование нового суждения, находящегося в отношении противоречия к исходному суждению. Отрицание атрибутивного суждения производится по закономерностям: А = О ;

Е = I ;

I = Е ;

О = А

2.3. УМОЗАКЛЮЧЕНИЕ

Умозаключение – основной, центральный элемент рассуждения - форма мышления, посредством которой получают новое суждение на основе одного или более известных суждений.

Значение умозаключения в том, что оно не только связывает знания в комплексы, но и обогащает, усиливает их. Умозаключение используется как способ познания прошлого, которое нельзя наблюдать непосредственно и для понимания будущего, которое еще нельзя наблюдать, т.е. это предвидение, прогнозы, тенденции развития.

Оно состоит из двух элементов: посылок - исходных суждений, на основании которых получается новое суждение и заключения, которое является следствием.

Суждение – выполняет функцию либо посылки, либо заключения. Понятие – выступает в роли S, либо Р.

Пример: «Все научные сведения полезны.

Химические сведения научны.

Химические сведения полезны».

Заключение подобно суждению может быть либо истинным, либо ложным, оно истинно, если выполняются два условия: посылки истинны по содержанию и вывод правильный по строению.

Если заключение находится после посылок, то перед ним ставятся слова «Следовательно», «Значит», Итак». Если перед посылками, то после него ставятся слова «Потому что», «Так как», «Ибо», «От того, что», «То». Если между посылками, то перед ним и после него употребляются соответствующие слова одновременно.

Умозаключений выделяют по разным признакам: по числу посылок; по видам и типам суждения; по степени вероятности. Исходя из сущности формы мышления, т.е. в зависимости от направления хода мысли можно выделить три коренных типа: дедукцию – заключение от более общего знания к менее общему; индукцию – от менее общего знания к более общему; традукцию – посылки и заключение одной степени общности.

Дедуктивные выводы, делятся на непосредственные и опосредованные, в зависимости от числа посылок: в первом случае заключение получается из одной посылки, во втором - из двух или более посылок.

ДЕДУКЦИЯ. НЕПОСРЕДСТВЕННЫЙ ВЫВОД