
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы фазового пространства
Методы фазового пространства относятся к наиболее ранним точным аналитическим методам теории нелинейных систем. К ним относится метод фазовой плоскости и метод точечных отображений или преобразований. Фазовым пространством называется пространство, по осям координат которого отложены переменные, характеризующие состояние динамической системы. Если движение системы описывается дифференциальным уравнением n-го порядка, то состояние этой системы в любой момент времени можно характеризовать некоторой точкой n-мерного фазового пространства, по осям которого отложены одна из координат системы и (n-1) ее производных. Точка, характеризующая состояние системы, называется изображающей точкой. При движении системы изображающая точка описывает в фазовом пространстве некоторую кривую, называемую фазовой траекторией. Каждому определенному переходному процессу в фазовом пространстве соответствует определенная фазовая траектория. Начальное положение изображающей точки определяется начальными условиями. В установившемся равновесном состоянии системы все производные рассматриваемой переменной равны нулю; соответствующие этому точки фазового пространства находятся в покое и называются особыми точками. Совокупность фазовых траекторий для всевозможных начальных отклонений называется фазовым портретом системы. Имея фазовый портрет системы, определяют по нему особые точки и траектории, исследуют устойчивость системы и оценивают качество процесса управления. Метод фазовой плоскости используется для исследования систем второго порядка и заключается в построении фазовых портретов на плоскости. Для этого из уравнений состояния исключается время и определяются уравнения фазовых кривых. Задача становится достаточно простой, если рассматривается система с кусочно-линейной характеристикой нелинейного элемента. В этом случае в разных областях фазовой плоскости система описывается линейными уравнениями, в соответствии с которыми строятся фазовые траектории, которые в дальнейшем “сшиваются” по линиям переключения, определяемым видом нелинейной характеристики. При исследовании нелинейных систем высокого порядка их аппроксимируют системами второго порядка с эквивалентным запаздыванием.
Для изображения процессов на фазовой плоскости нелинейное уравнение, описывающее систему, заменяют эквивалентными уравнениями первого порядка вида
где x, y - координата системы и ее первая производная; f(x, y) - нелинейная функция. Разделив первое из уравнений (6.39) на второе, получим дифференциальное уравнение, из которого исключено время t:
Решение данного уравнения y = F (x) (6.41) определяет уравнение фазовой траектории, которая графически изображается на фазовой плоскости (x, y). Каждой совокупности начальных условий (x0, y0) соответствует свое решение и своя фазовая траектория. Семейство фазовых траекторий характеризует все возможные виды переходных процессов в данной системе управления при любых начальных условиях и образует ее фазовый портрет. Основные свойства фазовых траекторий вытекают из выражения (6.40): 1) если f(x, y) определена и непрерывна в некоторой области и имеет непрерывные частные производные по своим аргументам, то через всякую точку фазовой плоскости, за исключением особых точек, проходит единственная фазовая траектория. Это означает, что фазовые траектории не пересекаются между собой; 2) так как при y>0 производная dx/dt>0 и x только возрастает, то в верхней фазовой полуплоскости при возрастании времени t изображающая точка движется слева направо. Соответственно в нижней полуплоскости движение происходит справа налево. Направление движения на траекториях показывают стрелками; 3) в точках, где y=0, f(x, y)¹0 (неособых точках на оси абсцисс), фазовые траектории пересекают ось под прямым углом. В тех случаях, когда решение уравнения (6.40) аналитическими методами затруднительно или невыполнимо, фазовые траектории можно построить приблизительным графическим методом изоклин. Изоклины представляют собой геометрическое место всех точек фазовой плоскости, для которых наклон фазовой траектории равен постоянному значению сi, то есть dy/dx=ci. Тогда вместо (6.40) можно написать уравнение
из которого получается уравнение изоклины
y = j(x, ci ). Задавая различные значения сi наклона касательных к фазовым траекториям, пересекающим эти изоклины, строят семейство изоклин, которые используются для построения фазовых траекторий (рис. 6.11). Фазовая траектория в точке пересечения с изоклиной имеет угол наклона arctg сi . В качестве примера на
Рис. 6.11
Рассмотрим фазовые траектории линейной системы второго порядка, переходный процесс в которой описывается уравнением
Введя обозначение для скорости изменения регулируемой величины y =
откуда, исключив время t, находим дифференциальное уравнение для определения фазовых траекторий
Решение y = F (x) этого уравнения определяет уравнения фазовых траекторий на фазовой плоскости (x, y). Возможные виды фазовых портретов системы, соответствующие корням характеристического уравнения p2 + a1p + a2 = 0, приведены в таблице.
Т а б л и ц а Виды фазовых портретов для линейных систем второго порядка
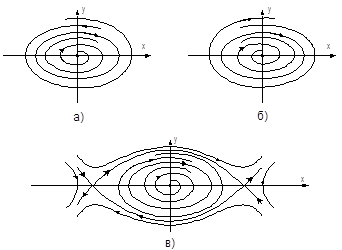
Вид и расположение фазовых траекторий, а также направление движения по ним изображающей точки дают возможность судить о характере движения системы и его устойчивости при различных начальных отклонениях. Особые точки и их характер определяют состояние равновесия исходной системы. Реальные автоматические системы можно считать линейными в предположении малости отклонений переменных от их установившихся значений. За пределами указанной области картина фазовых траекторий может стать качественно иной. В частности, если по линейной теории система неустойчивая и процесс расходится, то может оказаться, что из-за фактической нелинейности характеристик он не будет расходящимся неограниченно. Картина фазовых траекторий для такой системы изображена на рис. 6.12,а. Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе, но далее они приближаются асимптотически к замкнутому контуру ограниченных размеров. К нему же приближаются и все спирали, находящиеся вне контура. Такого рода замкнутый контур представляет собой особый вид линий на фазовой плоскости и называется устойчивым предельным циклом. Устойчивый предельный цикл соответствует автоколебаниям системы. Размеры предельного цикла представляют амплитуды колебаний самой величины x и скорости ее изменения y. Для определения периода автоколебаний необходимо решить уравнение системы во времени.
Рис. 6.12
Замкнутые фазовые траектории на фазовой плоскости называются предельными циклами, которые могут быть как устойчивыми (рис. 6.12,а), так и неустойчивыми (рис. 6.12,б). К этим предельным циклам стремятся изображающие точки при различных начальных отклонениях по различным фазовым траекториям. В различных частях фазовой плоскости фазовые траектории нелинейной системы могут быть различными (рис. 6.12,в). Линии, разделяющие фазовую плоскость на участки с различными фазовыми траекториями, называются сепаратрисами. Поведение системы в каждой области фазовой плоскости описывается своим дифференциальным уравнением.
Кроме того, для фазового портрета нелинейных систем с разрывными характеристиками характерно наличие линий переключения, которые также разделяют фазовую плоскость на ряд областей с различными фазовыми траекториями. При этом начальные значения переменных на каждом участке определяются через их конечные значения на предыдущем участке. Линии переключения характеризуются узловыми точками разрывных характеристик нелинейных элементов. Замечание: координатами (x, y) фазовой плоскости могут служить не обязательно отклонение (ошибка) управляемой величины системы и ее скорость. Для этой цели могут быть взяты любые две переменные, однозначно характеризующие состояние системы второго порядка в произвольный момент времени. Пример. Изобразим на фазовой плоскости переходный процесс и автоколебания в автоматической системе (рис. 6.1), линейная часть которой задана передаточной функцией
где k - коэффициент передачи; T - постоянная времени, а нелинейный элемент - статической характеристикой yн = F(x). Решение. В качестве координат фазовой плоскости выбираем отклонение управляемой величины x и скорость ее изменения y = dx/dt. Запишем для ошибки x дифференциальное уравнение системы, описывающее ее свободное движение
которое заменяем эквивалентными уравнениями первого порядка
Разделив первое из уравнений (6.43) на второе, получаем дифференциальное уравнение фазовых траекторий
решение, которого определяется характеристикой нелинейного элемента. Рассмотрим фазовые портреты системы для некоторых типов нелинейных элементов. 1. Идеальное двухпозиционное реле (рис. 6.4, а) со статической характеристикой F(x) = c sign (x). Дифференциальное уравнение (6.44) фазовых траекторий в этом случае примет вид
Переключение идеального реле происходит при x = 0. Следовательно, линия переключения на фазовой плоскости (рис. 6.13, а) совпадает с осью ординат. Справа от линии переключения при x > 0 дифференциальное уравнение фазовых траекторий будет
Его интегрирование дает уравнение фазовой траектории [2]
x = kcT ln ½y + kc½ - Ty + c0, (6.47)
где c0 - постоянная интегрирования, определяемая начальными условиями. Каждому конкретному c0 соответствует определенная кривая на фазовой плоскости справа от линии переключения. Эти кривые имеют асимптоту y = -kc.
Слева от линии переключения при x < 0 дифференциальное уравнение (6.45) фазовых траекторий принимает вид
что дает решение x = -kcT ln ½y - kc½ - Ty + c0, (6.49) согласно которому наносится семейство фазовых траекторий с асимптотой y = kc в левой фазовой полуплоскости. На рис. 6.13, а изображены фазовые траектории системы для начальных условий (x0, 0).
Рис. 6.13 2. Двухпозиционное реле с гистерезисом (рис. 6.4, в) со статической характеристикой
Переключение реле с гистерезисом происходит при x = +b, если y > 0 (линия AB на рис. 6.13, б); если же y < 0, то при x = -b (линия CD). Соответственно, линия переключения ABCD на фазовой плоскости (рис. 6.13, б) имеет разрыв. Справа от линии переключения ABCD справедливо дифференциальное уравнение фазовых траекторий (6.46), а слева - (6.48). Следовательно, фазовые траектории рассматриваемой системы (рис. 6.13, б) строятся аналогично предыдущему случаю. В данной системе будут наблюдаться устойчивые автоколебания, к которым сходится переходный процесс с обеих сторон, т.е. при любых начальных условиях. Амплитуда автоколебаний изображена на рис. 6.16, б отрезком a; отрезок yM изображает амплитуду скорости. Период автоколебаний определяется решением уравнений во времени. 3. Трехпозиционное реле с зоной нечувствительности (рис. 6.4, б) со статической характеристикой
Переключение трехпозиционного реле с зоной нечувствительности происходит при x = -b (линия AB фазовой плоскости на рис. 6.14, а) и при x = +b (линия CD). Соответственно, линии переключения AB и CD разделяют фазовую плоскость на на три области (рис. 6.14, а). Справа от линии переключения CD справедливо дифференциальное уравнение фазовых траекторий (6.46), а слева от линии переключения AB - (6.48). Следовательно, для рассматриваемой системы фазовые траектории в этих областях фазовой плоскости (рис. 6.14, а) строятся аналогично предыдущим случаям. В средней области при -b £ x £ +b, соответствующей зоне нечувствительности реле, дифференциальное уравнение (6.44) фазовых траекторий принимает вид
откуда
согласно которому семейство фазовых траекторий образуется отрезками прямых линий с отрицательным угловым коэффициентом -1/T.
Рис. 6.14
На рис. 6.14, а изображены фазовые траектории системы для начальных условий (x0, 0). Система приходит в положение равновесия при значениях ошибки, определяемой зоной нечувствительности реле. 4. Усилитель с насыщением (рис. 6.3, а) со статической характеристикой
Для построения фазовых траекторий нелинейной системы с кусочно-линейной характеристикой нелинейного элемента фазовую плоскость разделяем на области линиями AB и CD (рис. 6.14,б). Как следует из сравнения статических характеристик нелинейных элементов, фазовые траектории в правой и левой областях фазовой плоскости рассматриваемой системы строятся аналогично предыдущему случаю.
В средней области при -b £ x £ +b, соответствующей линейному участку характеристики, система становится линейной и дифференциальное уравнение (6.44) фазовых траекторий принимает вид
На рис. 6.14, б приведена фазовая траектория системы для начальных условий (x0, 0) в случае ее устойчивости в линейной области. Метод точечных преобразований (метод Пуанкаре-Андронова) позволяет установить существование автоколебаний в нелинейной системе второго порядка без построения фазовых траекторий. Сущность метода заключается в том, что для исследования динамики системы необходимо выяснить, как в зависимости от начальных условий перемещаются точки пересечения фазовой траектории с некоторой полупрямой, например, отрезком 0X фазовой плоскости (рис. 6.15).
Рис. 6.15
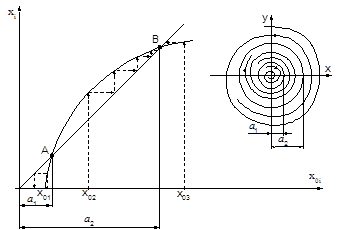
Возьмем начальное положение изображающей точки (x0, 0) где-нибудь на полуоси 0X. После обхода вокруг начала координат изображающая точка пересекает полуось 0X в точках x1, x2 и т.д. Последовательность точек пересечения фазовой траектории с выбранной полупрямой представляет точечное преобразование полупрямой самой в себя. Задавая различные начальные положения x0i изображающей точки на полуоси 0X, согласно уравнениям системы определяют соответствующие им точки xi на той же полуоси после обхода начала координат. Полученная таким образом зависимость xi = f (x0i) (6.53) называется функцией соответствия и используется для исследования периодических режимов в нелинейных системах.
Рис. 6.16
Для исследования возможных автоколебаний в координатах функции соответствия (рис. 6.16) проводится прямая из начала координат под углом 450 к координатным осям, для которой xi = x0i, что соответствует отображению каждой точки полуоси 0X самой в себя, т.е. после обхода вокруг начала координат точка возвращается в исходное положение. Пересечение кривой xi = f (x0i) с прямой Чтобы определить, какому типу предельного цикла это соответствует, надо взять на оси абсцисс начальную точку x0 сначала слева, а затем справа от точки пересечения и проследить ход точечного преобразования, как показано стрелками на рис. 6.16. Рис. 6.16 соответствует двум предельным циклам, из которых меньший (точка A) неустойчив, а больший (точка B) устойчив. Следовательно, при начальных условиях (x0, y0), расположенных внутри меньшего предельного цикла, система устойчива, а при всяких других начальных условиях она стремится к установившемуся автоколебательному процессу. Пересечение кривой xi = f (x0i) с прямой xi = x0i (точки A и B) определяют существование предельного цикла. Если указанная кривая и прямая не пересекаются, то автоколебания невозможны, а если касаются, то имеет место один предельный цикл. Чтобы определить, какому типу предельного цикла это соответствует, надо взять на оси абсцисс начальную точку x0 сначала слева, а затем справа от точки пересечения и проследить ход точечного преобразования, как показано стрелками на рис. 6.16. Рис. 6.16 соответствует двум предельным циклам, из которых меньший (точка A) неустойчив, а больший (точка B) устойчив. Следовательно, при начальных условиях (x0, y0), расположенных внутри меньшего предельного цикла, система устойчива, а при всяких других начальных условиях она стремится к установившемуся автоколебательному процессу. Коррекция нелинейных систем
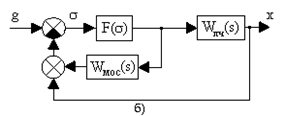
При коррекции нелинейных автоматических систем обычно решаются две основные задачи: обеспечение устойчивости системы; получение автоколебаний с заданной амплитудой и частотой. Коррекция осуществляется с помощью включения линейных или нелинейных корректирующих устройств, а также компенсацией влияния нелинейностей. Корректирующие устройства. В качестве линейных корректирующих устройств используются главным образом неединичные главные обратные связи (рис. 6.17, а) и местные обратные связи, охватывающие нелинейные элементы (рис. 6.17, б). Нелинейные корректирующие устройства включаются либо последовательно, либо в обратные связи. При расчете корректирующих устройств структурную схему нелинейной системы необходимо привести к эквивалентной одноконтурной схеме с нелинейным элементом и эквивалентной линейной частью с передаточной функцией для схемы, приведенной на рис. 6.17, а, Wэлч(s) = Wлч(s) ´Wос(s) и для схемы, приведенной на рис. 6.17, б, Wэлч(s) = Wлч(s) + Wмос(s).
Рис. 6.17
Влияние линейного корректирующего устройства на фазовый портрет системы. Рассмотрим систему, представленную на рис. 6.17, а, линейная часть которой задана передаточной функцией
где k - коэффициент передачи; T - постоянная времени, а нелинейный элемент - статической характеристикой F(s); у которой в качестве линейного корректирующего устройства включено в главную обратную связь форсирующее звено с передаточной функцией Wос(s) = (Tос s + 1), где Tос - постоянная времени. Передаточная функция эквивалентной линейной части системы будет
На основании структурной схемы (рис. 6.20,а) и выражения (6.54) свободное движение нелинейной системы (g = 0) можно описать дифференциальным уравнением относительно отклонения s (Ts2 + s)s + k(Tос s + 1)F(s) = 0, где s=d/dt. (6.55) Учитывая, что s = -(Tос s + 1)x, (6.56) получим дифференциальное уравнение относительно управляемой величины x системы
Для построения фазового портрета в качестве координат фазовой плоскости выбираем управляемую величину x и скорость ее изменения y = dx/dt и уравнение (6.57) заменяем эквивалентными уравнениями первого порядка
откуда дифференциальное уравнение фазовых траекторий будет
Если нелинейным элементом является усилитель с насыщением (рис. 6.3, а), то для линейного участка характеристики ½s½£ b F(s) = kу s = - kу(Tос s + 1)x и, следовательно,
Поскольку для участков насыщения F(s) = ±c, то вместо (6.59) аналогично (6.46) и (6.48) получим уравнения:
Так как линейная область на фазовой плоскости определяется неравенством ½s½£ b и зависимостью (6.56), то уравнения граничных линий можно записать в виде:
Следовательно, граничные линии проходят через точки на оси абсцисс a = arctg На рис. 6.18, а изображены фазовые траектории и граничные линии для системы при начальных условиях (x0, 0). Таким образом, при неединичной обратной связи фазовый портрет в зонах насыщения, определяемый уравнениями (6.61) и (6.62), будет таким же, как и при единичной обратной связи. В области линейной части характеристики фазовый портрет системы определяется уравнением (6.60), в котором имеется дополнительный член, обусловленный постоянной времени звена обратной связи Tос. Кроме того, наличие производной в главной обратной связи поворачивает граничные линии, разделяющие фазовую плоскость на области, против часовой стрелки навстречу движению изображающей точки. Угол поворота этих линий тем больше, чем больше постоянная времени Tос; в случае единичной обратной связи (Tос = 0) угол поворота равняется нулю, при этом угол наклона a = 900.
Рис. 6.18 Если нелинейный элемент обладает релейной характеристикой, то фазовые траектории в зонах насыщения и нечувствительности определяются такими же уравнениями, как и в случае единичной обратной связи. Однако наличие члена Tосs в передаточной функции звена обратной связи обуславливает поворот линий переключения реле влево соответственно уравнениям (6.63); при этом угол наклона a определяется по формуле (6.64). На рис. 6.18, б показана фазовая траектория и линии переключения для нелинейной системы с трехпозиционным реле с зоной нечувствительности (рис. 6.4, б) при начальных условиях (x0, 0). Поворот линий переключения реле навстречу движению изображающей точки фазовой траектории обеспечивает работу системы с упреждением. Путем подбора постоянной времени Tос можно обеспечить перевод релейной системы в новое состояние за одно включение реле, как показано на рис. 6.4, б, при угле наклона линий переключения, равном В том случае, когда система имеет неединичную жесткую главную обратную связь вида Wос(s) = 1 + kос, (6.65) имеет место s = -(1 + kос)x. (6.66) Граничные линии и линии переключения для такой главной обратной связи определяются уравнениями:
Отсюда следует, что неединичная жесткая главная обратная связь вызывает перемещение граничных линий и линий переключения без изменения угла их наклона, что позволяет изменять соотношения между областями с различными фазовыми траекториями на фазовой плоскости, например, изменять область нечувствительности системы при неизменности зоны нечувствительности реле или усилителя. Компенсация влияния нелинейности. При компенсации нелинейностей нелинейную систему можно рассматривать как линейную относительно определенных входных воздействий. Компенсирующие нелинейности. Линеаризация заданной нелинейности F(s) заключается во включении последовательно или параллельно компенсирующего нелинейного элемента с обратной нелинейной характеристикой F-1(s). При этом получаем эквивалентный линейный элемент. На рис. 6.19 приведен пример линеаризации усилителя с зоной нечувствительности путем включения параллельно с ним усилителя с насыщением.
Рис. 6.19
Если нелинейность F(s) присутствует в объекте управления ОУ, то линеаризация системы может быть осуществлена путем параллельного включения объекту управления компенсирующей нелинейности F-1(s) и модели его линейной части Wм лч оу(s) (рис. 6.20).
Рис. 6.20 Вибрационная компенсация нелинейностейзаключается в том, что нелинейный элемент приобретает свойства пропорциональности, если на его вход вместе с полезным медленно изменяющимся сигналом g(t) подается высокочастотная периодическая составляющая u(t) (рис. 6.21). Если на входе нелинейного элемента (рис. 6.21, а, б) с характеристикой F(x) действует полезный медленно изменяющийся сигнал g(t) совместно с несмещенным периодическим сигналом u(t), частота w которого достаточно велика, чтобы можно было приближенно считать функцию g(t) постоянной в пределах периода T = 2p/w (рис. 6.21, б), т.е. x(t) = g(t) + u(t), (6.68) то выходной сигнал можно представить в виде суммы средней, медленно изменяющейся составляющей F1(g) и колебательной функции F2(u), близкой к периодической с частотой w
yн = F(x) = F[g(t) + u(t)] = F1(g) + F2(u). (6.69)
Среднюю составляющую приближенно можно представить как среднее значение выходного сигнала нелинейного элемента за период
В случае g = const формула (6.70) точная и определяет постоянный член ряда Фурье, составленного относительно выходного сигнала нелинейного элемента, а колебательная функция F2(u) есть сумма гармонических составляющих этого ряда.
Рис. 6.21 Формула (6.70) тем точнее, чем больше частота w и чем меньше g(t) изменяется в пределах периода T. На рис. 6.21, в представлена характеристика F1(g) для идеального двухпозиционного реле при компенсирующей периодической функции u(t) треугольного вида частоты w и амплитуды A. Статическая характеристика является линейной для полезного сигнала g(t), изменяющегося в пределах ±A. Коэффициент передачи линейной части определяется как
Таким образом, чем больше амплитуда компенсирующих колебаний A, тем шире зона линейности нелинейного элемента. Однако при этом уменьшается коэффициент передачи линеаризованного элемента. Статическая характеристика F1(g) может быть получена экспериментальным путем, что позволяет определить значения kу и A. Выходной сигнал нелинейного элемента yн (6.69) поступает на вход линейной части системы. При достаточно большой частоте w периодического сигнала u(t) линейная часть из-за инерционности не пропускает компенсирующие колебания, поэтому составляющей F2(u) можно пренебречь. Следовательно, для разомкнутой системы (рис. 6.21, а) можно определить передаточную функцию
W(s) = kу Wлч(s). (6.72) Это значит, что при задающем воздействии g(t) < A (рис. 6.24, в) для частоты w компенсирующих колебаний u(t), превышающих частоту среза линейной части системы, нелинейная система может рассматриваться как линейная. Для формирования высокочастотного сигнала u(t) используется или специальный генератор или собственные колебания системы.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 997; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.124.232 (0.128 с.) |
 (6.39)
(6.39) . (6.40)
. (6.40)

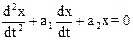 .
.
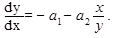


















 ,
,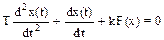 , (6.42)
, (6.42) (6.43)
(6.43) (6.44)
(6.44)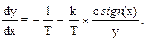 (6.45)
(6.45)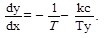 (6.46)
(6.46) (6.48)
(6.48)



 (6.50)
(6.50) , (6.51)
, (6.51)


 . (6.52)
. (6.52)

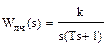 ,
, . (6.54)
. (6.54) . (6.57)
. (6.57) (6.58)
(6.58)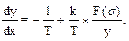 (6.59)
(6.59) . (6.60)
. (6.60) при s < -b и (Tос s + 1)x > +b; (6.61)
при s < -b и (Tос s + 1)x > +b; (6.61) при s > +b и (Tос s + 1)x < -b. (6.62)
при s > +b и (Tос s + 1)x < -b. (6.62) (6.63)
(6.63) . (6.64)
. (6.64)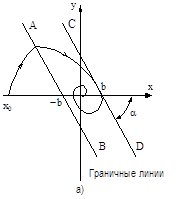

 .
. (6.67)
(6.67)

 . (6.70)
. (6.70)

 (6.71)
(6.71)


