
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ориентированные графы непрерывных САУ
Наряду со структурными схемами для графического изображения моделей САУ широко используются ориентированные графы, которые в ряде случаев благодаря своим наглядности и прозрачности позволяют легче, чем структурные схемы, провести необходимые преобразования, значительно упрощающие решение задач анализа и синтеза САУ. Ориентированным графом называется множество точек, называемых вершинами и множества самонепересекающихся ориентированных кривых, называемых дугами, которые подчиняются следующим трем правилам: 1) каждая незамкнутая дуга содержит только две вершины; 2) каждая замкнутая дуга содержит только одну вершину; 3) дуги не имеют общих точек, кроме вершин. Ориентированный граф САУ имеет кроме того следующие свойства: 1) каждая дуга соответствует звену модели САУ и характеризуется оператором изображаемого его звена; 2) каждая вершина соответствует какой-либо переменной структурной схемы. Граф системы управления может быть построен по структурной схеме. При переходе от структурной схемы к ориентированному графу необходимо следовать следующим правилам: 1) знаки суммирования сигналов в элементах суммирования учитываются в операторах соответствующих дуг; 2) каждый элемент суммирования заменяется вершиной, которой ставится в соответствие выходная переменная звена; 3) каждое звено структурной схемы заменяется дугой с оператором звена; 4) каждой переменной внешних воздействий соответствует своя вершина. Так структурной схеме (рис. 3.13, а) соответствует граф, показанный на рис. 3.13, б.
g y g 1 W 1 -1 W 2 y
- W 3
a) б) Рис. 3.13 При построение графа, эквивалентного структурной схеме дискретной системы, дополнительно к четырем выше сформулированным правилам пользуется специфическим правилом: дискретные элементы изображаются как и на структурной схеме ключами с учетом, что передаточные функции формирующих звеньев объединены с операторами других непрерывных звеньев (рис. 3.14, где W 1(s)= W ф3(s) W (s)).
g e e *(t) y g 1 e e * W 1(s) y
- W ос(s) a) б) Ориентированные графы могут быть преобразованы с использованием следующих правил: 1) параллельные дуги можно заменить одной дугой с передачей равной сумме передач исходных дуг;
2) путь, не содержащий не принадлежащих ему дуг, можно заменить одной дугой с передачей равной произведению передач отдельных дуг этого пути. Для упрощения сложного графа и вычисления по нему передачи между двумя любыми вершинами используется правило Мэйсона, выражаемое следующей формулой: Wx,y =
Здесь Wi – передача i -го пути от вершины x к вершине y, равная произведению передач дуг, входящих в этот путь; m - число таких путей;
где W 0 j, W o k , W o l – передачи j -го, k -го или l -го контуров, равные произведению передач входящих в них дуг; в первой сумме суммируются передачи всех контуров, во второй сумме – произведения передач несоприкасающихся (не имеющих общих вершин) контуров; в третьей сумме суммируются произведения трех передач трех несоприкасающихся контуров и так далее;
В качестве примера рассмотрим использование формулы Мэйсона для графа, изображенного на рис. 3.15. W 9
1 W 1 W 3 W 5 1 W 7 g - W 4 y - W 8
Представленный граф содержит: 1) два пути от вершин G к вершине Y W п1 = W 1 W 3 W 5 W 7, W п2= W 5 W 7 W 9; 2) пять простых контуров: W 01 = – W 1 W 2, W 02 = – W 3 W 4, W 03 = – W 5 W 6, W 04 = – W 7, W 05 = – W 1 W 3 W 5 W 7 W 8 3) четыре пары несоприкасающихся контуров: W 01 W 03, W 01 W 04, W 02 W 04, W 03 W 04; 4) одну тройку несоприкасающихся контуров W 01 W 03 W 04;
5) определитель подграфа первого пути 6) определитель подграфа второго пути: определитель всего графа
+ (W 01 W 03 + W 01 W 04 + W 02 W 04 + W 03 W 04) – W 01 W 03 W 04. Передача всего графа от вершин G к вершине Y: Wg,y =
Описание систем управления моделями пространства состояний Уравнения состояния САУ
Пространство состояний САУ это бесконечная совокупность временных моментов состояния системы, описанная конечной совокупностью переменных состояния. Число переменных состояния обычно принимается равным порядку общего дифференцированного уравнения системы, т.е. числу дифференцированных уравнений 1-го порядка.
Уравнения состояния записываются обычно в нормальной форме Коши и имеют вид:
В левой части уравнения состояния всегда производная переменной состояния, а в правой части сумма всех переменных состояния и внешних воздействий со своими коэффициентами. Полное описание в пространстве состояния будет представлять систему из n дифференцированных уравнений 1-го порядка в форме Коши. Существует три способа записи уравнений состояния подобной формы: 1) запись уравнения в форме Коши на этапе первичного поэлементного описания системы управления; например, уравнение напряжений цепи якоря двигателя постоянного тока
где r яц и L яц – сопротивление и индуктивность якорной цепи соответственно,
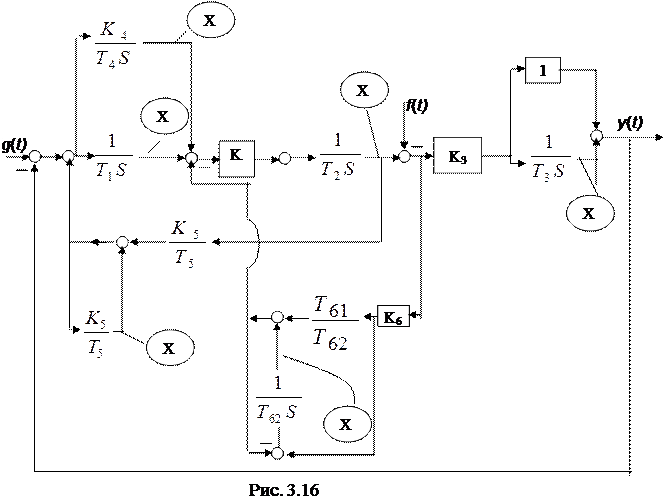
2) Запись уравнений состояний по передаточным функциям звеньев; например для передаточной функции W (s) = В случае сложной передаточной функции порядка n > 1 прибегают к разложению ее на сумму слагаемых 1-го порядка, либо к представлению в виде произведения сомножителей 1-го порядка. 3) Универсальным способом записи уравнений состояния является их составление на основе детализированной структурной схемы системы. Процесс записи уравнений включает в себя 2 этапа: - выбор переменных состояния; в качестве переменных состояния выбираются выходные переменные интегрирующих звеньев ДСС; - запись уравнений для входных переменных интегрирующих звеньев. Для иллюстрации процесса записи уравнений состояния по ДСС покажем систему нормальных уравнений для ДСС, представленной на рис. 3.16. В кружках на схеме показаны переменные состояния.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.21 (0.014 с.) |
 f f
f f
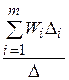 .
. - определитель графа, вычисляемый по формуле:
- определитель графа, вычисляемый по формуле: +
+  –
–  +…,
+…, - W 2 - W 6 -1
- W 2 - W 6 -1 = 1, так как нет контуров, несоприкасающихся с первым путем;
= 1, так как нет контуров, несоприкасающихся с первым путем; = 1 + W 1 W 2;
= 1 + W 1 W 2; .
. = ai 1 x 1 + ai 2 +… + ainxn + bi 1 u 1 + bi 2 u 2 + … + bimum, i = 1, 2, …, n.
= ai 1 x 1 + ai 2 +… + ainxn + bi 1 u 1 + bi 2 u 2 + … + bimum, i = 1, 2, …, n. =
=  –
–  +
+  .
. =
=  можно записать уравнение TsY (s) + Y (s) = kU (s) и после перехода во временную область T
можно записать уравнение TsY (s) + Y (s) = kU (s) и после перехода во временную область T 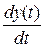 + y (t) = ku (t), и уравнение состояния
+ y (t) = ku (t), и уравнение состояния  .
.
 =
= 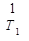 (-(
(-(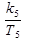 x 2 - x 5) + g - x 3 - k 3(x 3 - f)),
x 2 - x 5) + g - x 3 - k 3(x 3 - f)), =
=  (x 2 - f))),
(x 2 - f))), 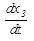 =
=  (x 2 - f),
(x 2 - f), =
=  (g - x 3 - k 3(x 2 - f) - (x 5 +
(g - x 3 - k 3(x 2 - f) - (x 5 +  =
=  (- x 5 +
(- x 5 +  =
=  (k 6(x 2 - f) - x 6 - k 6
(k 6(x 2 - f) - x 6 - k 6 


