Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение функции одной переменнойСтр 1 из 5Следующая ⇒
Определение функции одной переменной Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f (x) с областью определения X = D (f) и областью значения Y = E (f). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией. Частным значением функции y = f (x) при фиксированном значении аргумента x = x0 называют y0 = f (x0). Графиком функции y = f (x) называют геометрическое место точек M (x;f (x)) на плоскости Oxy, где x Î D (f) и f (x) Î E (f). Определение Пусть функция y = f (U) определена на множестве D (f), а функция U = g (x) определена на D (g), причём E (g) Тогда функция y = F (x) = f (g (x)) называется сложной функцией (или функцией от функции, или суперпозицией функций f и g). Определение Пусть задана функция y = f (x) взаимно однозначно отображающая множество X = D (f) на множество Y = E (f). Тогда функция x = g (y) называется обратной к функции y = f (x), т. е. любому y Предел функции в точке. Определение: Число b называется пределом функции в точке при x → x0, если для любой последовательности точек {xn}∞n=1 ϵ D и стремится к точке x0, последовательность соответствующих значений функции {yn} будет стремиться к числу b.
Геометрическая интерпретация. Предел функции Односторонние пределы Определение Число А называется правым (левым) пределом функции y = f (x) в точке x 0, если для любого малого числа ε > 0 найдётся другое малое число При этом используют следующие обозначения:
Бесконечно малые и их основные свойства. Бесконечно большие функции. Ограниченные функции. Связь между бесконечно малыми и бесконечно большими функциями. Разложение функции, имеющей предел, на постоянную и бесконечно малую. Теоремы о пределах.
Бесконечно малые и бесконечно большие функции Определение. Функция a(x) называется бесконечно малой при x ® x 0или в точке Определение. Функция f (x) называется бесконечно большой в точке Определение. Функция f (x) называется ограниченной на некотором множестве X Ì D (f), если существует такое число M > 0, что для любого x Î X выполняется неравенство | f (x)| < M. 2. Теорема (о связи между бесконечно малой функцией в точке x0 и бесконечно большой функцией в точке x0) Если функция f (x ) является бесконечно большой в точке Теорема о разложении функции, имеющей предел на постоянную и бесконечно малую функцию. Теорема. Если функция ƒ(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции α(х), т. е. если limƒ(х)=А, при Х→Хо то ƒ(х)=А+а(х). Теоремы о пределах. 1) 2) 3) 4) 5)
Первый и второй замечательные пределы. Сравнение бесконечно малых функций. Эквивалентные функции. Первый замечательный предел: Предел функции Второй замечательный предел: Предел функции
Сравнение бесконечно малых функций: α(x), β(x) - бесконечно малые функции
Эквивалентные функции:
Непрерывность функции в точке и на отрезке. Точки разрыва, их классификация. Теоремы о непрерывных функциях. Функций (c u) ’ = c u’, d (c u) = c du, (c – const);
(u ± v) ’ = u’ ± v’, d (u ± v) = du ± dv; (u v) ’ = u’ v + u v’, d (u v) = v du + u dv;
Таблица производных основных элементарных функций 1. (c)' = 0 2. (x a)' = a× x a – 1 3. (ax)' = ax ×ln a, (a > 0, a ≠ 1) 4. (ex)' = ex 5. (lo ga x)' = 6. (ln x)' = 7. (sin x)' =cos x 8. (cos x)' = – sin x 9. (tg x)' = 10. (ctg x)' = – 11. (arcsin x)' = 12. (arccos x)' = – 13. (arctg x)' = (arcctg x)' = Теорема Ролля Теорема 4 (теорема Ролля). Если функция f (x) определена на отрезке [ a; b ] и выполнены следующие условия: · f (x) непрерывна на отрезке [ a; b ]; · f (x) дифференцируема на интервале (a; b); · f (a) = f (b), то внутри этого отрезка [ a; b ] найдется хотя бы одна точка х 0, в которой выполняется равенство: f '(х 0) = 0. Теорема Лагранжа Теорема 5 (теорема Лагранжа). Если функция f (x) определена на отрезке [ a; b ] и выполнены следующие условия: · f (x) непрерывна на отрезке [ a; b ], · f (x) дифференцируема на интервале (a; b), то внутри этого отрезка существует хотя бы одна точка х 0, в которой выполняется равенство: f ' (х 0) =
Теорема Коши Теорема 6 (теорема Коши). Если функции f (x) и g (x) определены на отрезке [ a; b ] и удовлетворяют условиям: · f (x) и g (x) непрерывны на отрезке [ a; b ]; · f (x) и g (x) дифференцируемы на интервале (a; b); · g '(x) ¹ 0 при любом x Î (a; b), то внутри отрезка [ a; b ] найдётся хотя бы одна точка х 0, в которой выполняется равенство:
Правило Лопиталя Теорема 7 (правило Лопиталя). Если функции f (x) и g (x) определены в некоторой окрестности точки х 0 и в этой окрестности они удовлетворяют условиям: · f (x) и g (x) дифференцируемы в каждой точке за исключением может быть самой точки х 0; · g '(x) ¹ 0 для любого x из этой окрестности; · тогда, если существует
Замечание 1. Правило Лопиталя используется для раскрытия неопределённостей типа Замечание 2. Если к условиям теоремы 7 добавить дифференцируемость функций f '(x) и g '(x) в окрестности точки х 0, то при выполнении остальных требований для f '(x) и g '(x) правило Лопиталя можно применить повторно. Асимптоты плоской кривой Определение 1. Если точка M (x; y) перемещается по кривой y = f (x) так, что хотя бы одна из координат точки стремится к ¥ и при этом расстояние от этой точки до некоторой прямой стремится к 0, то эта прямая называется асимптотой кривой y = f (x). Асимптоты бывают двух видов: вертикальные и наклонные. Определение 2. Прямая x = a называется вертикальной асимптотой кривой y = f (x), если хотя бы один из односторонних пределов Замечание. Если прямая x = a является вертикальной асимптотой кривой y = f (x), то в точке x = a функция f (x) имеет разрыв второго рода. Наоборот, если в точке x = a функция f (x) имеет разрыв второго рода, то прямая x = a является вертикальной асимптотой кривой y = f (x). Определение 3. Прямая
где Теорема 1. Для того чтобы кривая y = f (x) имела наклонную асимптоту при
Монотонность функции Определение 4. Функция y = f (x) называется возрастающей (убывающей) на промежутке (a; b), если для любых x 1 и x 2, принадлежащих этому промежутку, из условия x 2 > x 1 следует неравенство:
f (x 2) > f (x 1) (f (x 2) < f (x 1)).
Определение 5. Функция y = f (x) называется монотонной на промежутке (a; b), если она на этом промежутке является только возрастающей или только убывающей. Теорема 2 (достаточные условия монотонности). Если функция y = f (x) дифференцируема на промежутке (a; b) и f’ (x) > 0 (f’ (x) < 0) для любых x Î (a; b), то функция возрастает (убывает) на этом промежутке. Экстремумы функции Определение 6. Функция y = f (x) имеет в точке x 0Î D (f) максимум y m ax (минимум y min), если существует такая окрестность точки x 0, в которой для всех x выполняется неравенство:
f (x 0) > f (x) (f (x 0) < f (x)). Определение 7. Точки максимума и минимума функции называются точками экстремума функции. Теорема 3 (необходимое условие экстремума). Если функция y = f (x) имеет экстремум в точке x 0, то в этой точке производная функции равна нулю или не существует. Теорема 4 (достаточное условие экстремума). Если функция y = f (x) непрерывна в точке x 0, дифференцируема в некоторой её окрестности, за исключением может быть самой этой точки, f’ (x 0) = 0 или не существует и при переходе x через точку x 0 производная f '(x) изменяет знак, то точка x 0 является точкой экстремума. Если при этом знак f '(x) меняется с + на –, то x 0 – точка максимума, с – на +, то x 0 – точка минимума. Основные понятия. Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
Частные производные. Определение. Частной производной по x от функции z=f(x,y) называется предел отношения частного приращения
Частная производная обозначается одним из символов Аналогично определяется частная производная по y: Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного. Частные производные функции любого числа переменных определяют 3. Геометрическая интерпретация частных производных функции двух Переменных
Аналогично, частная производная плоскостью x=const.
13. Полный дифференциал функции нескольких переменных, его применение в приближённых вычислениях, достаточное условие дифференцируемости. Формула полного дифференциала функции нескольких переменных:
d2z=z’x’x*d2x+ z’y’y*d2y Формула приближенного вычисления: z=z(x, y); Dz = dz; dx=Dx; dy=Dy z (x, y)»z(M0)+z’x(M0)*Dx+ z’y(M0)*Dy Достаточное условие дифференцируемости: Если функция z=(x; у) имеет непрерывные частные производные 14. Уравнения касательной плоскости и нормали к поверхности. Дифференцирование сложных и неявных функций. (неявная функция) (явная функция) Уравнение касательной: F’x(M0)*(x-x0)+ F’y(M0)*(y-y0)+ F’z(M0)*(z-z0)=0 z’x(M0)*(x-x0)+ z’y(M0)*(y-y0)=(z-z0) Уравнение нормали: N̅={F’x; F’y; F’z} N̅={z’x; z’y -1} (x-x0)/ F’x(M0)= (y-y0)/ F’y(M0)= (z-z0)/ F’z(M0) (x-x0)/ z’x(M0)= (y-y0)/ z’y(M0)= (z-z0)/ (-1) Дифференцирование: (сложные функции) (неявной функции F(x, y, z)=0) 1. z=z(x, y), x=x(t) => z=z(t)) z’x= -(F’x/F’z) y=y(t) z’y= -(F’y/F’z) dz/dt=z’x*x’t+ z’y*y’t 2. z=z(x, y), y=y(x) => z=z(x) dz/dx=z’x+ z’y*y’x 3. z=z(x, y), x=x(u, v) => z=z(u, v) y=y(u, v) ∂z/∂u= z’u= z’x*x’u+ z’y*y’u ∂z/∂v= z’v= z’x*x’v+ z’y*y’v 15. Производные высших порядков функции нескольких переменных. z=z(x, y) z’x, z’y – первого порядка z’x’x, z’y’y, z’x’y, z’y’x – второго порядка z’x’y= z’y’x 16. Экстремум функции нескольких переменных. Необходимое и достаточное условия экстремума. 1. Найти частные производные z’x и z’y. Составить и решить систему уравнений z’x=0 z’y=0 Точки, координаты которых удовлетворяют указанной системе, называют стационарными. 2. Найти А=z’x’x, С=z’y’y, В=z’x’y и вычислить значение Δ=А*С-В2 в каждой стационарной точке. После этого использовать следующую схему: · Если Δ>0 и А>0, то в исследуемая точка есть точкой минимума. · Если Δ>0 и А<0, то в исследуемая точка есть точкой максимума. · Если Δ<0, то в рассматриваемой стационарной точке экстремума нет. · Если Δ=0, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование. Интегрирование дробей
1. Если степень числителя больше или равна степени знаменателя, то дробь неправильная и нужно поделить уголком, тем самым выделив целую часть:
2. Знаменатель разложить на множители и привести всю дробь к сумме простых дробей:
I. II. III. а) б) Разложить знаменатель на множители и решать, используя пределы Ао, Во. Интегрирование тригонометрии 1. Интегралы вида ∫cos(m*(x))sin(n*(x))dx находят в зависимости от четности степеней m и n следующим образом: а) если m или n нечетное, то используют замену переменной: t=sinx, при нечетном m; t=cosx, при нечетном n, и формулу sin2x+cos2x=1; б) если m и n четные, то используют формулы понижения степени:
в) Если m+n=−2k, k∈N т. е. m+n является целым четным отрицательным числом, то удобно использовать подстановки tgx=t и ctgx=t. 2. Интегралы вида ∫sin(m*(x))cos(n*(x))dx, ∫cos(m*(x))cos(n*(x))dx, ∫sin(m*(x))sin(n*(x))dx вычисляют с помощью преобразований подынтегральной функции по следующим формулам: sin(m*(x))cos(n*(x))dx = sin(m*(x))sin(n*(x))dx = cos(m*(x))cos(n*(x))dx = 4. Интегралы вида, R(sinx,cosx)dx где R(u,v)− рациональная функция двух переменных, приводят к интегралам от рациональных функций нового аргумента t подстановкой t=tg(x/2). При этом используются формулы
Если под интегралом sinx и cosx содержатся только в четных степенях, то удобнее использовать подстановку tgx=t.
Интегрирование иррациональности
Т. о среднем. Если функция f (x) непрерывна на отрезке [ a;b ], то на этом отрезке найдётся хотя бы одна точка c, в которой выполняется равенство:
Формула Ньютона–Лейбница Теорема. Пусть функция f (x) непрерывна на отрезке [ a;b ] и F(x) – какая-либо её первообразная на отрезке [ a;b ]. Тогда определённый интеграл от функции f (x) по отрезку [ a;b ] равен разности значений функции F(x) в точках b и a:
Определение функции одной переменной Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f (x) с областью определения X = D (f) и областью значения Y = E (f). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией. Частным значением функции y = f (x) при фиксированном значении аргумента x = x0 называют y0 = f (x0). Графиком функции y = f (x) называют геометрическое место точек M (x;f (x)) на плоскости Oxy, где x Î D (f) и f (x) Î E (f). Определение Пусть функция y = f (U) определена на множестве D (f), а функция U = g (x) определена на D (g), причём E (g) Тогда функция y = F (x) = f (g (x)) называется сложной функцией (или функцией от функции, или суперпозицией функций f и g). Определение Пусть задана функция y = f (x) взаимно однозначно отображающая множество X = D (f) на множество Y = E (f). Тогда функция x = g (y) называется обратной к функции y = f (x), т. е. любому y Предел функции в точке. Определение: Число b называется пределом функции в точке при x → x0, если для любой последовательности точек {xn}∞n=1 ϵ D и стремится к точке x0, последовательность соответствующих значений функции {yn} будет стремиться к числу b.
Геометрическая интерпретация. Предел функции Односторонние пределы Определение Число А называется правым (левым) пределом функции y = f (x) в точке x 0, если для любого малого числа ε > 0 найдётся другое малое число При этом используют следующие обозначения:
Бесконечно малые и их основные свойства. Бесконечно большие функции. Ограниченные функции. Связь между бесконечно малыми и бесконечно большими функциями. Разложение функции, имеющей предел, на постоянную и бесконечно малую. Теоремы о пределах.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.162.247 (0.175 с.) |
 D (f).
D (f). E (f) соответствует единственное значение x
E (f) соответствует единственное значение x 
 в точке
в точке  существует и равен
существует и равен  , если для любой
, если для любой  -окрестности точки
-окрестности точки  -окрестность точки
-окрестность точки  , что для любого
, что для любого  из этой
из этой 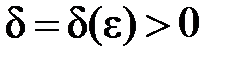 – такое, что для всех
– такое, что для всех 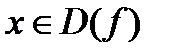 и лежащих в правой (левой) окрестности точки x 0, т.е.
и лежащих в правой (левой) окрестности точки x 0, т.е.  , справедливо неравенство:
, справедливо неравенство:  .
. – для правого предела.
– для правого предела. – для левого предела.
– для левого предела. ,если пределa(x)при x®
,если пределa(x)при x®  .
. удовлетворяющего неравенству
удовлетворяющего неравенству  , выполняется неравенство | f (x)| > M.
, выполняется неравенство | f (x)| > M. является бесконечно малой в точке
является бесконечно малой в точке 
 т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).
т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).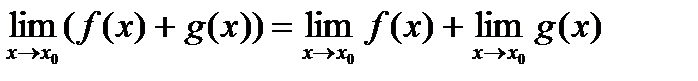

 , если g(x)≠0 в δ(x0)
, если g(x)≠0 в δ(x0)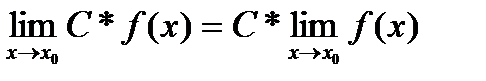 ;
; 

 в точке
в точке  существует и равен 1, т.е.
существует и равен 1, т.е. 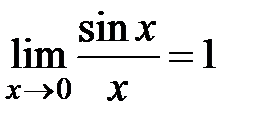 .
. при x
при x  существует и равен числу e, т.е.
существует и равен числу e, т.е. .
.


 - α
- α
 -1 ~ α
-1 ~ α
 -1 ~ α lna
-1 ~ α lna
 ~
~ 
 -1 ~
-1 ~ 
 -1 ~
-1 ~ 

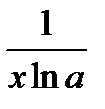 , (a > 0; a ≠ 1)
, (a > 0; a ≠ 1)


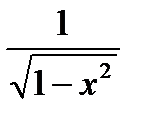



 .
. .
. или
или  ,
,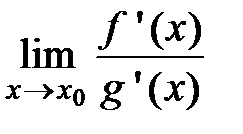 конечный или бесконечный, то выполняется равенство:
конечный или бесконечный, то выполняется равенство: =
=  .
. или
или  , возникающих при вычислении пределов. Если под знаком предела оказывается неопределённость другого типа: 0×∞,
, возникающих при вычислении пределов. Если под знаком предела оказывается неопределённость другого типа: 0×∞,  , 10, 00 или ∞0, то с помощью тождественных алгебраических преобразований такая неопределённость приводится к
, 10, 00 или ∞0, то с помощью тождественных алгебраических преобразований такая неопределённость приводится к  или
или  равен +¥ или – ¥.
равен +¥ или – ¥. называется наклонной асимптотой кривой
называется наклонной асимптотой кривой 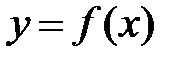 при
при 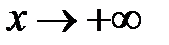 (или
(или  ), если функцию f (x) можно представить в виде:
), если функцию f (x) можно представить в виде: ,
, (x) – бесконечно малая функция при
(x) – бесконечно малая функция при 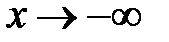 ).
). (или
(или  и
и 
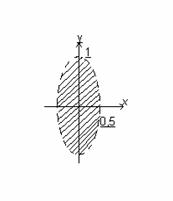 Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Функции двух переменных допускают графическую иллюстрацию. Графиком функции z = f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z = f (x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.
Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Функции двух переменных допускают графическую иллюстрацию. Графиком функции z = f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z = f (x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность. по x к приращению
по x к приращению  при стремлении
при стремлении 
 .
.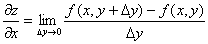 .
. Частная производная
Частная производная  численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.
численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.
 численно равна тангенсу угла наклона касательной к кривой, получающейся сечении поверхности z=f(x,y)
численно равна тангенсу угла наклона касательной к кривой, получающейся сечении поверхности z=f(x,y) или dz=z’x*dx+ z’y*dy или du=u’x*dx+ u’y*dy+ u’z*dz
или dz=z’x*dx+ z’y*dy или du=u’x*dx+ u’y*dy+ u’z*dz и
и  в точке М(х;у), то она дифференцируема в этой точке.
в точке М(х;у), то она дифференцируема в этой точке.
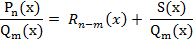
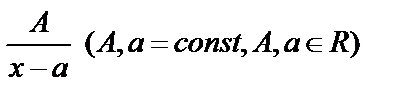 ,
, ,
, )D < 0
)D < 0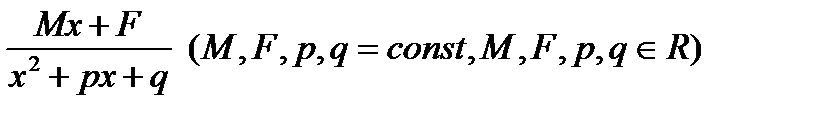 D > 0
D > 0

 ,
, .
.