
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базовые алгоритмы обработки разреженных матриц. Матричное умножение.
Прежде всего рассмотрим алгоритм умножения непосредственно по определению.
Определение предполагает, что элемент в строке i и столбце j матрицы C вычисляется как скалярное произведение i-ой строки матрицы A и j-го столбца матрицы B. Какие особенности вносит разреженное представление? Во-первых, используемая структура данных, построенная на основе формата CRS, предполагает хранение только ненулевых элементов, что усложняет программирование вычисления скалярного произведения, но одновременно уменьшает количество арифметических операций. При вычислении скалярных произведений нет необходимости умножать нули и накапливать полученный нуль в частичную сумму, что положительно влияет на сокращение времени счета. Пусть, например, в первом и втором векторах находится по 1% ненулевых элементов, при этом только десятая часть этих элементов расположена на соответствующих друг другу позициях. В этом случае расчет с использованием информации о структуре векторов может использовать в 1000 раз меньшее число умножений и сложений. Учитывая, что таких пар векторов Во-вторых, необходимо научиться выделять вектора в матрицах A и B. В соответствии с определением, речь идет о строках матрицы A и столбцах матрицы B. Выделить строку матрицы в формате CRS не представляет труда: i-я строка может быть легко найдена, так как ссылки на первый элемент poiner[i] и последний элемент (pointer[i+1]-1) известны, что позволяет получить доступ к значениям элементов и номерам столбцов, хранящихся в массивах values и cols соответственно. Таким образом, проход по строке выполняется за время, пропорциональное числу ненулевых элементов в указанной строке, а проход по всем строкам – за время, пропорциональное NZ, где NZ – количество ненулевых элементов в матрице. Проблема возникает с выделением столбца. Чтобы найти элементы столбца j необходимо просмотреть массив cols (~NZ операций) и выделить все элементы, у которых в соответствующей ячейке массива cols записано число j. Если это нужно проделать для каждого столбца, необходимо ~NZN операций, что является неэффективным.
Возможное, но не единственное решение проблемы состоит в транспонировании матрицы B: после вычисления В-третьих, необходимо научиться записывать посчитанные элементы в матрицу C. Учитывая, что C хранится в формате CRS, важно избежать перепаковок. Для этого нужно обеспечить пополнение матрицы C ненулевыми элементами последовательно, по строкам – слева направо, сверху вниз. Это означает, что часто используемый в вычислениях на бумаге метод "возьмем первый столбец матрицы B, запишем его над матрицей A и перемножим на все строки…" не подходит. Нужно делать наоборот – брать первую строку матрицы A и умножать ее по очереди на все столбцы матрицы B (строки матрицы Таким образом, для выполнения матричного умножения разреженных матриц необходимо сделать следующее: 1) Реализовать транспонирование разреженной матрицы и применить его к матрице B. 2) Инициализировать структуру данных для матрицы C, обеспечить возможность ее пополнения элементами. 3) Последовательно перемножить каждую строку матрицы A на каждую из строк матрицы Еще один непростой момент: в процессе вычисления скалярного произведения на бумаге (в точной арифметике) может получиться нуль, причем не только в том случае, когда при сопоставлении векторов соответствующих друг другу пар не обнаружилось, но и просто как естественный результат. В арифметике с плавающей точкой нуль может получиться еще и в связи с ограничениями на представление чисел и погрешностью вычислений (см. стандарт IEEE-754). Нули, получившиеся в процессе вычислений, можно как хранить в матрице C (в векторе values в соответствующей позиции), так и не хранить; оба подхода имеют право на существование.
Как следует из приведенного описания, основной операцией является скалярное произведение двух разреженных векторов (обозначим их Алгоритм подразумевает для каждой отличной от нуля компоненты вектора Заметим, что каждый умножаемый вектор является строкой матрицы и упорядочен в соответствии с выбранной структурой хранения матрицы. Это означает, что для сопоставления компонент может быть применен алгоритм, весьма похожий на слияние двух отсортированных массивов в один с сохранением упорядочивания. Алгоритм выглядит следующим образом: 1) Встать на начало обоих векторов (ks = …, ls = …) 2) Сравнить текущие элементы A.Col[ ks ], B.Col[ ls ]. Если значения совпадают, накопить в сумму произведение A.Value[ ks ] * B.Value[ ls ] и увеличить оба индекса, в противном случае – увеличить один из индексов, в зависимости от того, какое значение больше (например, A.Col[ ks ] > B.Col[ ls ] → ls++). Шаг2 выполняется до тех пор, пока не кончатся элементы хотя бы в одном из векторов. Данный алгоритм имеет линейную трудоемкость, но он не очень хорошо соответствует архитектуре компьютера, т.к. содержит очень много ветвлений.
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 898; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.162.179 (0.005 с.) |

 , получается существенное сокращение объема вычислений. К сожалению, не все так просто. Учет структуры векторов тоже требует машинного времени. Необходимо выполнить сопоставление номеров ненулевых элементов с целью обнаружения пар значений, которые необходимо перемножить и накопить в частичную сумму.
, получается существенное сокращение объема вычислений. К сожалению, не все так просто. Учет структуры векторов тоже требует машинного времени. Необходимо выполнить сопоставление номеров ненулевых элементов с целью обнаружения пар значений, которые необходимо перемножить и накопить в частичную сумму.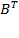 появится возможность эффективно работать со столбцами исходной матрицы B, а сам алгоритм транспонирования работает достаточно быстро. Другой вариант – для каждой CRSматрицы, которая может понадобиться в столбцовом представлении, дополнительно хранить транспонированный портрет. Сэкономив время на транспонировании, придется смириться с расходами времени на поддержание дополнительного портрета в актуальном состоянии. Есть и другие варианты решения проблемы, никак не связанные с транспонированием матрицы B. В дальнейшем мы будем использовать подход, основанный на транспонировании матрицы B.
появится возможность эффективно работать со столбцами исходной матрицы B, а сам алгоритм транспонирования работает достаточно быстро. Другой вариант – для каждой CRSматрицы, которая может понадобиться в столбцовом представлении, дополнительно хранить транспонированный портрет. Сэкономив время на транспонировании, придется смириться с расходами времени на поддержание дополнительного портрета в актуальном состоянии. Есть и другие варианты решения проблемы, никак не связанные с транспонированием матрицы B. В дальнейшем мы будем использовать подход, основанный на транспонировании матрицы B. , записывая в C полученные результаты и формируя ее структуру.
, записывая в C полученные результаты и формируя ее структуру.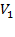 и
и 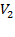 ), и к ее реализации нужно подойти с особой тщательностью.
), и к ее реализации нужно подойти с особой тщательностью.


