
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многошаговые разностные методы решения задачи Коши для обыкновенных дифференциальных уравнений
Рассмотрим задачу Коши для обыкновенного дифференциального уравнения
где Для решения задачи Коши для уравнения (1) при t >0 введем равномерную сетку с постоянным шагом t Введем понятие линейного m шагового разностного метода для решения задачи (6.10). Линейным m- шаговым методом называется система разностных уравнений
где: n=m,m +1...; Систему (6.11) будем рассматривать как рекуррентные соотношения, выражающие новое значения
Отсюда следует, что для начала расчета по формулам (6.11) надо знать m предыдущих значений функции y, причем y Отличие от одношаговых методов состоит в том, что по формулам (6.11) расчет ведется только в точках сетки.
Определение. Метод (6.11) называется явным, если коэффициент b
Обычно это уравнение решают методом Ньютона при начальном значении На практике используют частный случай методов (6.11), т.н. методы Адамса, т.е. когда производная
Это и есть методы Адамса. При b
6.2.1 Задача подбора числовых коэффициентов aк, bк
Выясним, как влияют коэффициенты ak, bk на погрешность аппроксимации уравнения (6.11), на устойчивость и сходимость.
Определение. Невязкой, или погрешностью аппроксимации методов (6.11) называется функция
где Если разложить функции
Из вида функции
где l =1,..., p. Условия (6.16) представляют собой СЛАУ относительно неизвестных Запишем систему (6.16) для методов Адамса
где l =2,..., p. Отсюда наивысший порядок аппроксимации для неявного метода p=m+ 1, для явного – p=m. 6.2.2 Устойчивость и сходимость многошаговых разностных методов
Наряду с системами уравнений (6.11) будем рассматривать т.н.
где n=m,m +1,.... Будем искать его решение в виде функции
где q -число подлежащее определению. Подставив
Уравнение (6.19) принято называть характеристическим уравнением для разностных методов (6.11). Говорят, что разностный метод (6.11) удовлетворяет условию корней, если все корни уравнения (6.19) Разностный метод (6.11), удовлетворяющий условию корней, называется устойчивым методом. Теорема. Пусть разностный метод (6.11) удовлетворяет условию корней и выполнено условие
где: Методы Адамса удовлетворяют условию корней, т.к. a0=-a1= 1, следовательно, q=q1= 1.
6.2.3 Примеры m -шаговых разностных методов Адамса для различных m
Явные методы. При m= 1 порядок точности p= 1. Тогда метод описывается формулой
В этом случае получаем метод Эйлера. При m= 2 порядок точности p= 2. Тогда метод описывается формулой
При m= 3 порядок точности p= 3. Тогда метод описывается формулой
При m= 4 порядок точности p= 4. Метод описывается формулой
Неявные формулы Адамса.
m= 1, p= 2, m= 2, p= 3, m= 3, p= 4,
Неявные методы содержат искомое значение
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.95.244 (0.013 с.) |
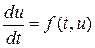 ,
,
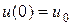 .
.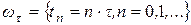 .
.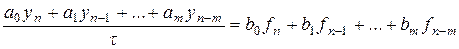 ,
,
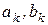 -числовые коэффициенты не зависящие от n; k =0,1,…, m.
-числовые коэффициенты не зависящие от n; k =0,1,…, m.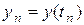 через ранее найденные значения
через ранее найденные значения 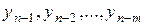 , причем расчет начинают с индекса n=m, т.е. с уравнения
, причем расчет начинают с индекса n=m, т.е. с уравнения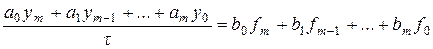 .
.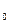 =u
=u 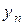 легко выражается через
легко выражается через 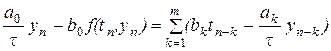 .
.
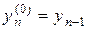 . Коэффициенты уравнения (6.11) определены с точностью до множителя, тогда, чтобы устранить этот произвол, вводят условие
. Коэффициенты уравнения (6.11) определены с точностью до множителя, тогда, чтобы устранить этот произвол, вводят условие 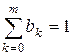 , с тем условием, что правая часть (6.11) аппроксимирует правую часть уравнения (6.10).
, с тем условием, что правая часть (6.11) аппроксимирует правую часть уравнения (6.10).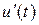 аппроксимируется разностным отношением, включающим две соседние точки
аппроксимируется разностным отношением, включающим две соседние точки 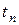 и
и 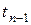 . Тогда
. Тогда 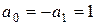 ;
; 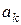 =0, k =2,..., m и
=0, k =2,..., m и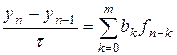 .
.
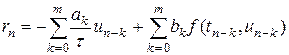 ,
,
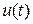 -точное решение дифференциального уравнения (6.10).
-точное решение дифференциального уравнения (6.10).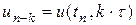 в ряд Тейлора в точках
в ряд Тейлора в точках 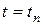 равномерной сетки, окончательно получим функцию
равномерной сетки, окончательно получим функцию
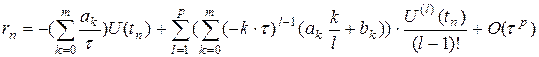 .
.
 следует, что порядок аппроксимации будет равен p, если выполнены условия
следует, что порядок аппроксимации будет равен p, если выполнены условия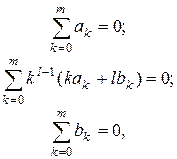
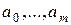 ,
, 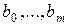 . Их количество равно 2(m +1). Решив систему (6.16), получаем неизвестные числовые коэффициенты. Для неявных методов наивысшим порядком аппроксимации p=2m, а для неявных – p=2m- 1.
. Их количество равно 2(m +1). Решив систему (6.16), получаем неизвестные числовые коэффициенты. Для неявных методов наивысшим порядком аппроксимации p=2m, а для неявных – p=2m- 1.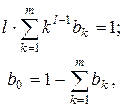
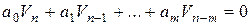 ,
,
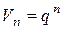 ,
,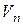 в (6.18) получаем уравнение для нахождения q
в (6.18) получаем уравнение для нахождения q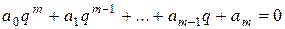 .
.
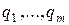 лежат внутри или на границе единичного круга комплексной плоскости, причем на границе нет кратных корней.
лежат внутри или на границе единичного круга комплексной плоскости, причем на границе нет кратных корней.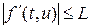
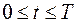 . Тогда при
. Тогда при 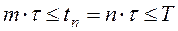 , n³m и достаточно малых t будет выполнена оценка
, n³m и достаточно малых t будет выполнена оценка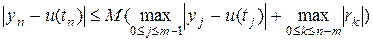 ,
,
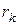 -погрешность аппроксимации;
-погрешность аппроксимации; 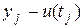 -погрешность в задании начальных условий; M=const.
-погрешность в задании начальных условий; M=const.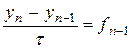 .
.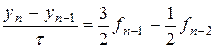 .
.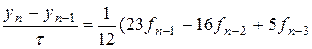 .
. 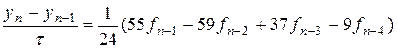 .
.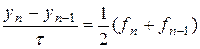 -метод трапеций;
-метод трапеций;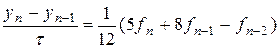 ;
;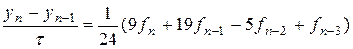 .
.


