Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплексный метод решения задачи линейного программирования.
Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом. Симплексный метод в отличие от геометрического универсален – с его помощью можно решить ЗЛП. В основу симплексного метода положена идея последовательного улучшения получаемого решения. Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (или, по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум). Таким образом, имея систему ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Процесс применения симплексного метода предполагает реализацию трех его основных элементов: 1) способ определения какого-либо первоначального допустимого базисного решения задачи; 2) правило перехода к лучшему (точнее, не худшему) решению; 3) критерий проверки оптимальности найденного решения. Симплексный метод включает в себя ряд этапов и может быть сформулирован в виде четкого алгоритма. Это позволяет успешно программировать и реализовывать его на ЭВМ. Задачи с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную. 10. Построение опорных планов. Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод). Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Симплекс-метод основан на следующих свойствах ЗЛП: 1. Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
2. Множество всех планов ЗЛП выпукло. 3. Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). 4. Каждой угловой точке многогранника решений отвечает опорный план ЗЛП. Пусть поставлена задача: найти min значение целевой функции
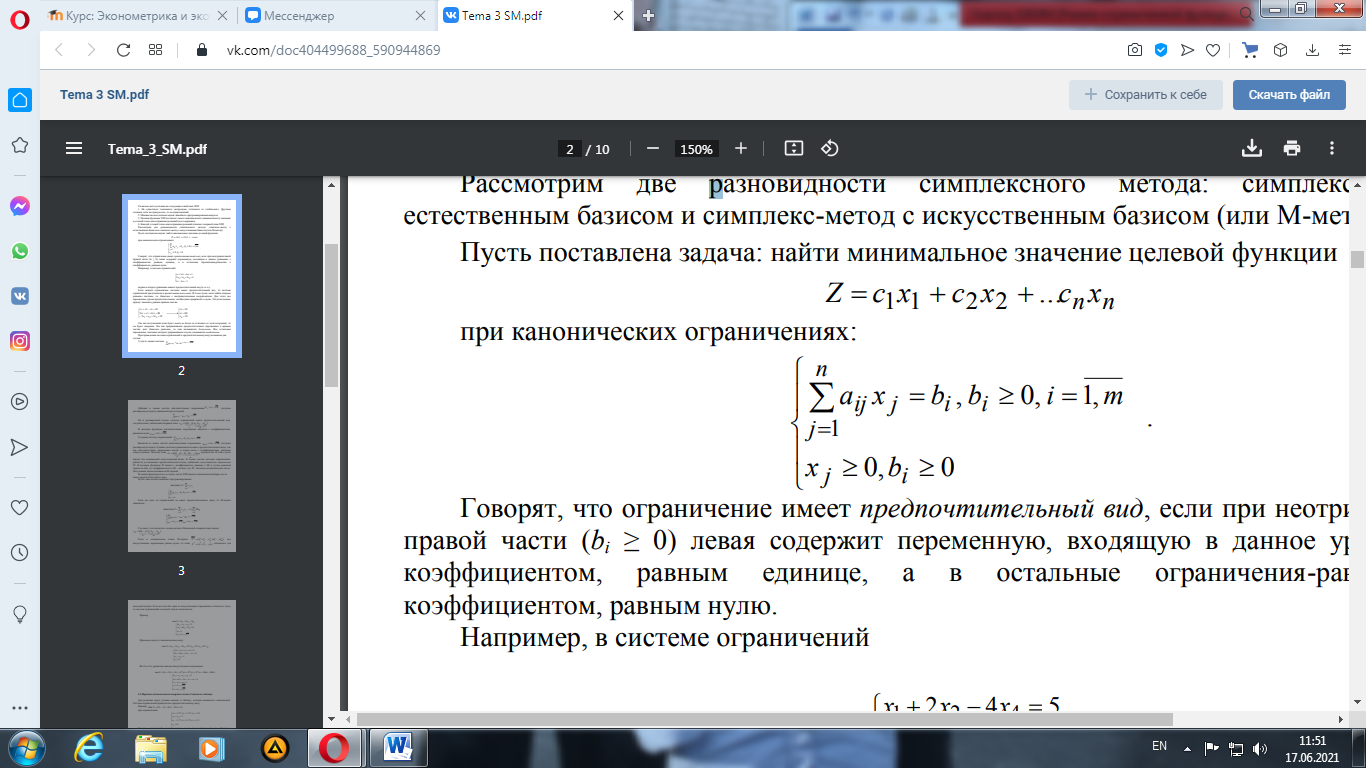
Говорят, что ограничение имеет предпочтительный вид, если при неотрицательной правой части (bi ≥ 0) левая содержит переменную, входящую в данное уравнение с коэффициентом, равным единице, а в остальные ограничения-равенства с коэффициентом, равным нулю. Если каждое ограничение системы имеет предпочтительный вид, то система ограничений представлена в предпочтительном виде. В этом случае легко найти опорное решение системы, т.е. базисное с неотрицательными координатами. Для этого все переменные, кроме предпочтительных, необходимо приравнять к нулю. Тогда последние примут значения, равные правым частям. Так как полученный план будет иметь не более m отличных от нуля координат, то он будет опорным. Так как приравнивание предпочтительных переменных к правым частям дает базисное решение, то они называются базисными. Все остальные переменные, значения которых приравниваем к нулю, называются свободными. При приведении системы ограничений к предпочтительному виду возможны два случая. 1) пусть задана система:
Добавив к левым частям дополнительные переменные
Но в расширенной задаче система ограничений имеет предпочтительный вид, следовательно, начальный опорный план: В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю: 2) задана система ограничений:
Вычитая из левых частей дополнительные переменные
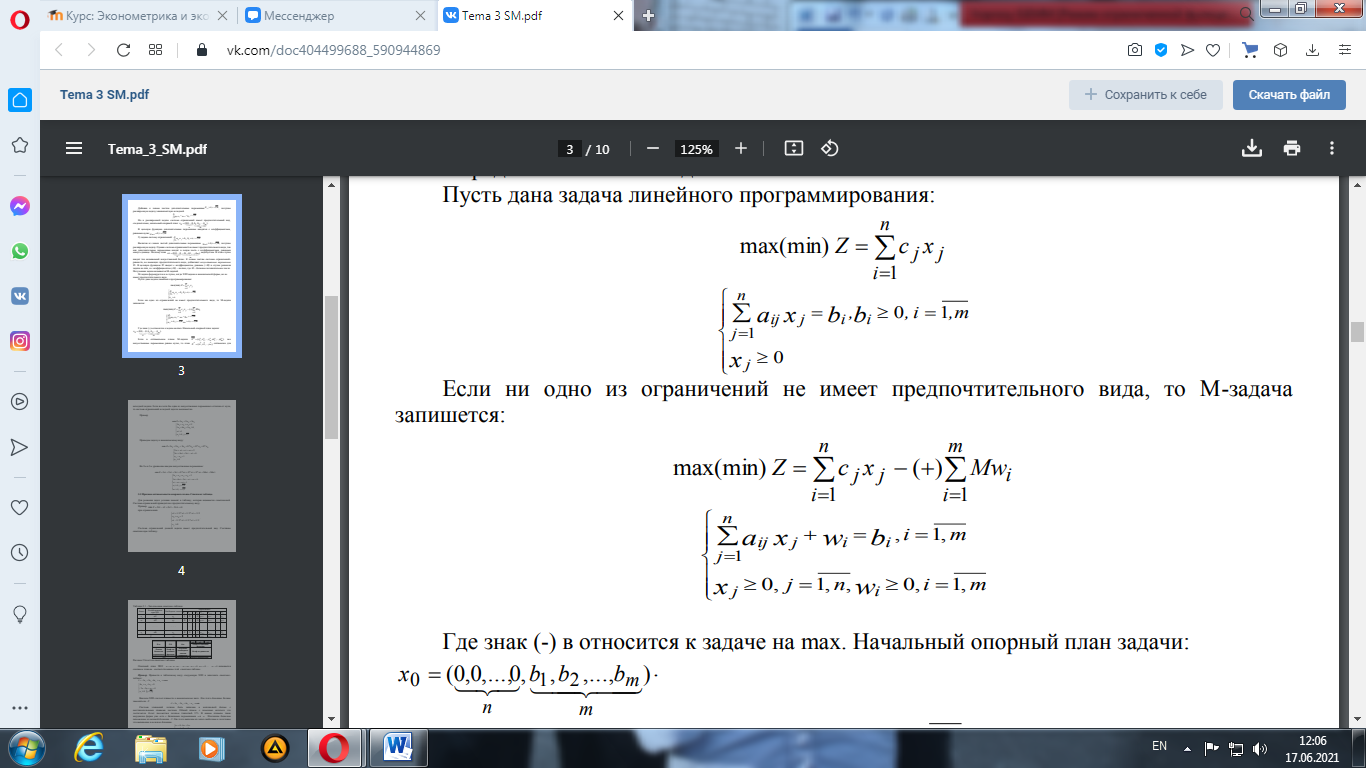
Полученная задача называется М-задачей. М-задача формируется и в случае, когда ЗЛП задана в канонической форме, но не имеет предпочтительного вида. Пусть дана задача линейного программирования:
Если ни одно из ограничений не имеет предпочтительного вида, то М-задача запишется:
Где знак (–) в относится к задаче на max. Начальный опорный план задачи:
Если в оптимальном плане М-задачи 11. Признак оптимальности опорного плана. Симплекс таблица. Для решения задач условия заносят в таблицу, которая называется симплексной. Система ограничений приводится к предпочтительному виду.
Система ограничений данной задачи имеет предпочтительный вид. Составим симплексную таблицу.
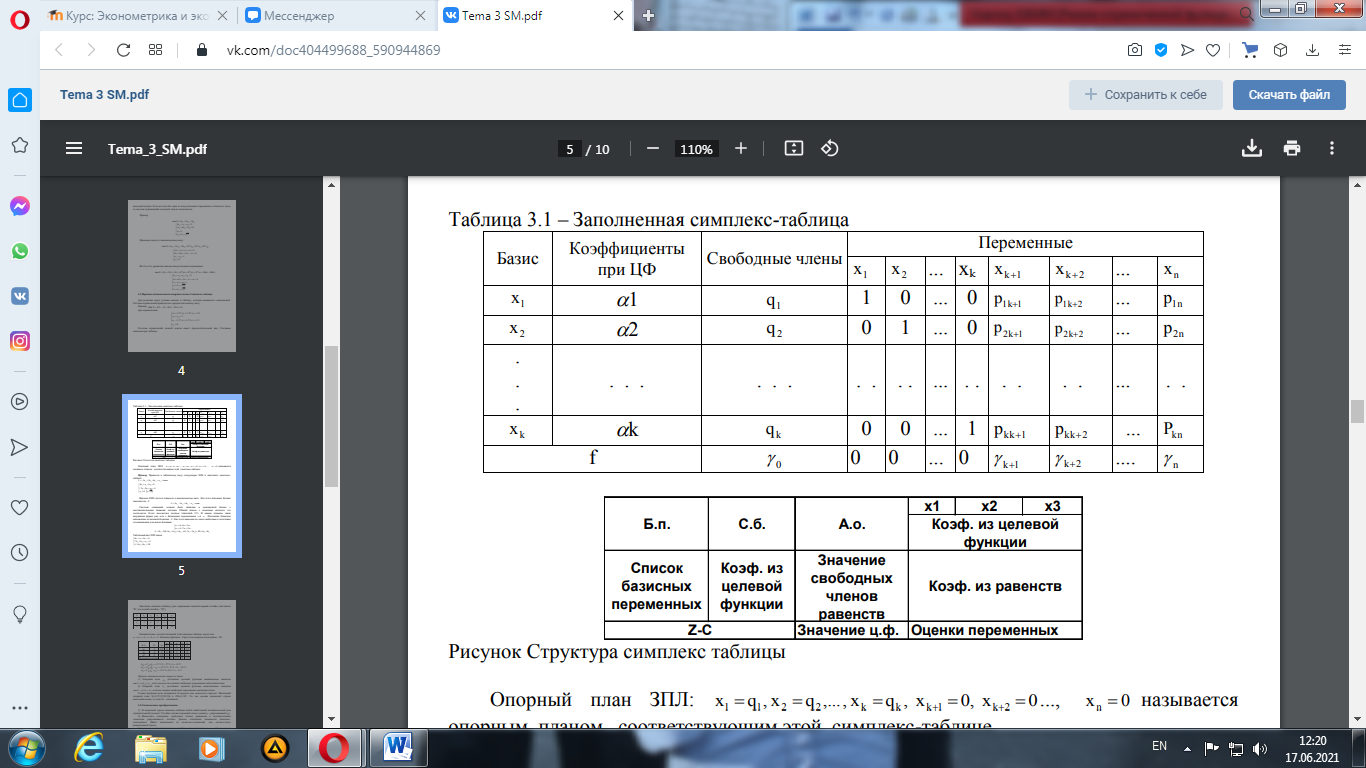
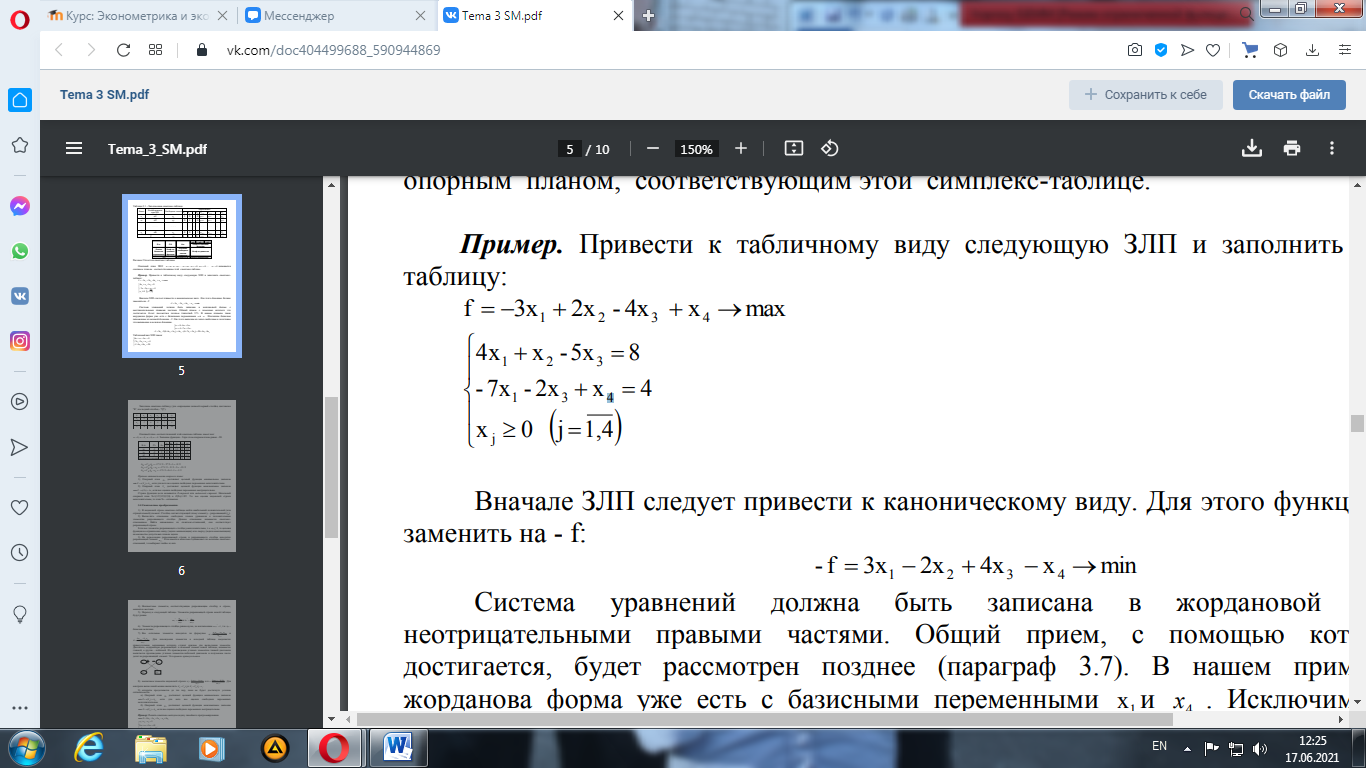
Опорный план ЗПЛ: Пример. Привести к табличному виду следующую ЗЛП и заполнить симплекстаблицу:
Вначале ЗЛП следует привести к каноническому виду. Для этого функцию fнужно заменить на - f:
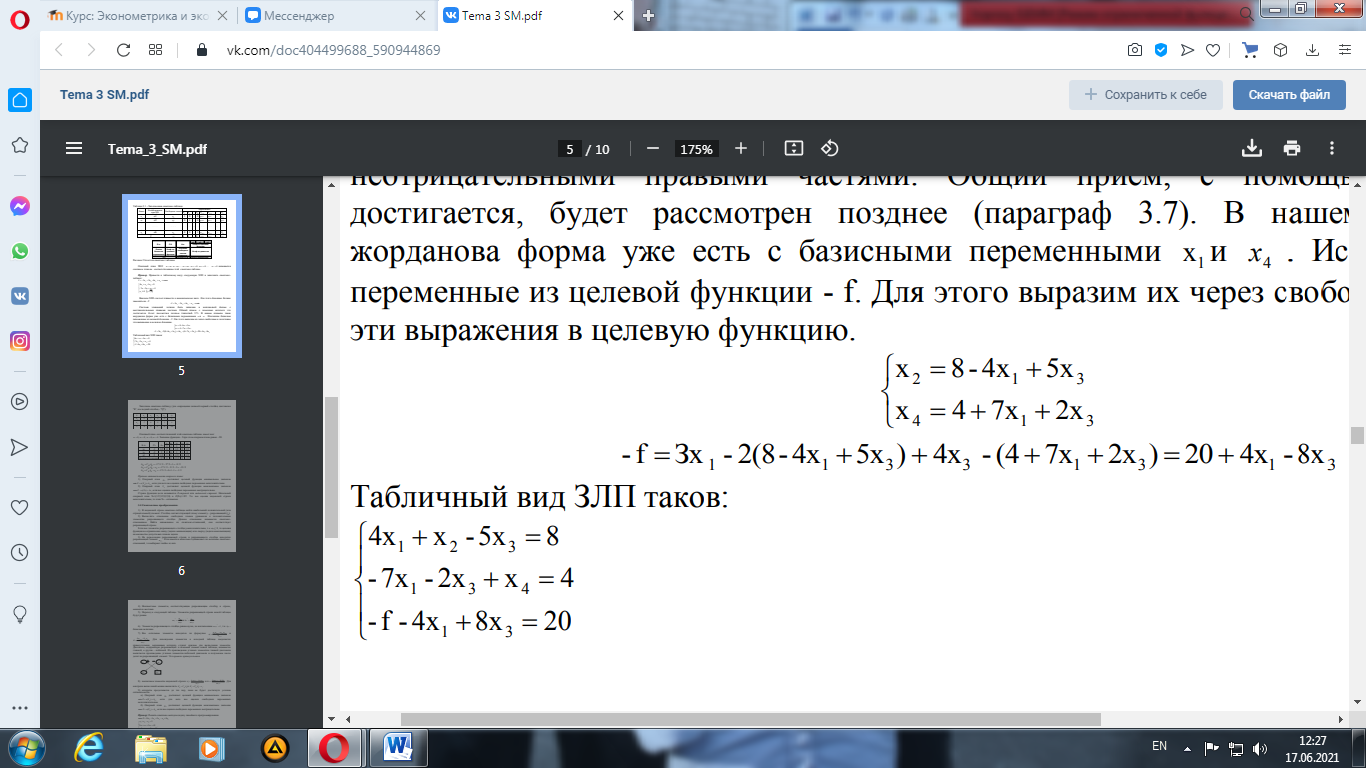
Система уравнений должна быть записана в жордановой форме с неотрицательными правыми частями. В нашем примере такая жорданова форма уже есть с базисными переменными х2 и х4. Исключим базисные переменные из целевой функции - f. Для этого выразим их через свободные и подставим эти выражения в целевую функцию.
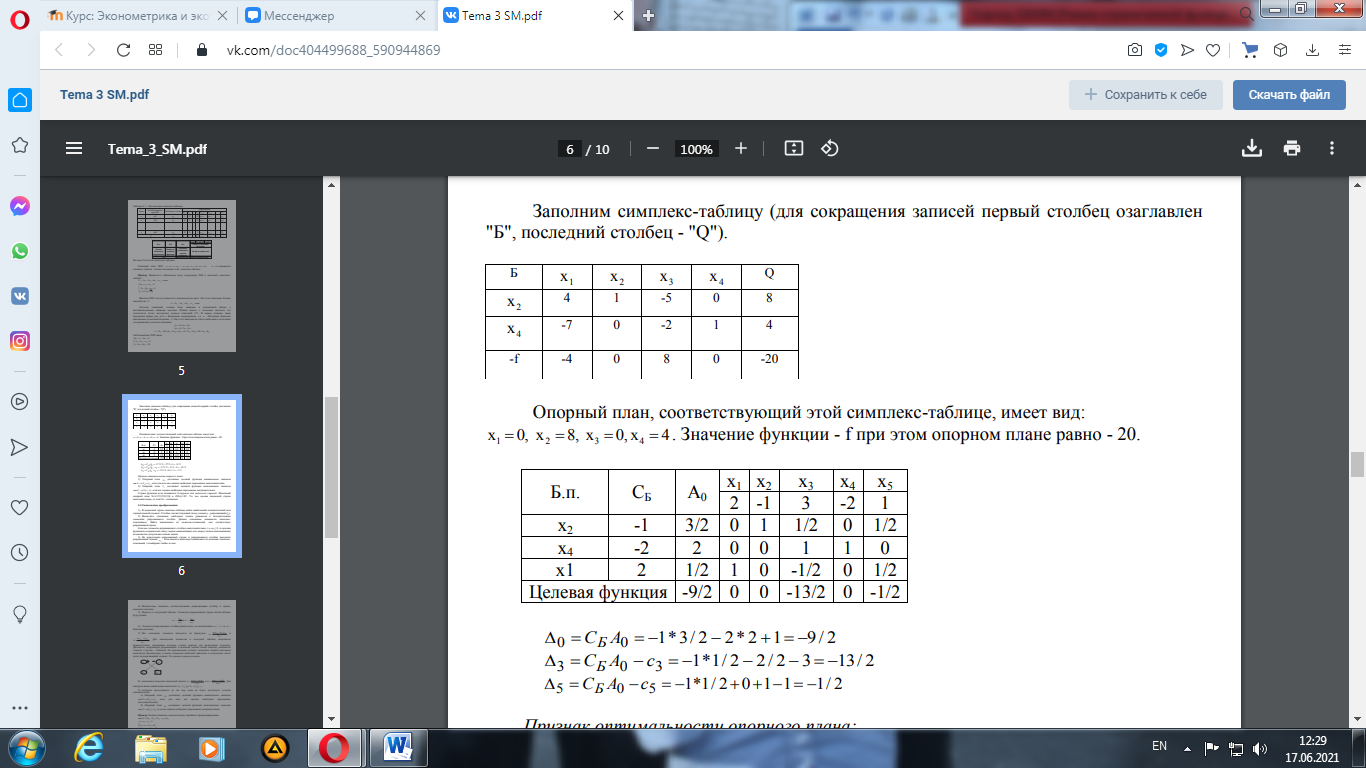
Заполним симплекс-таблицу (для сокращения записей первый столбец озаглавлен "Б", последний столбец - "Q").
Опорный план, соответствующий этой симплекс-таблице, имеет вид: х1 = 0, х2 = 8, х3 = 0, х4 = 4. Значение функции - f при этом опорном плане равно - 20.
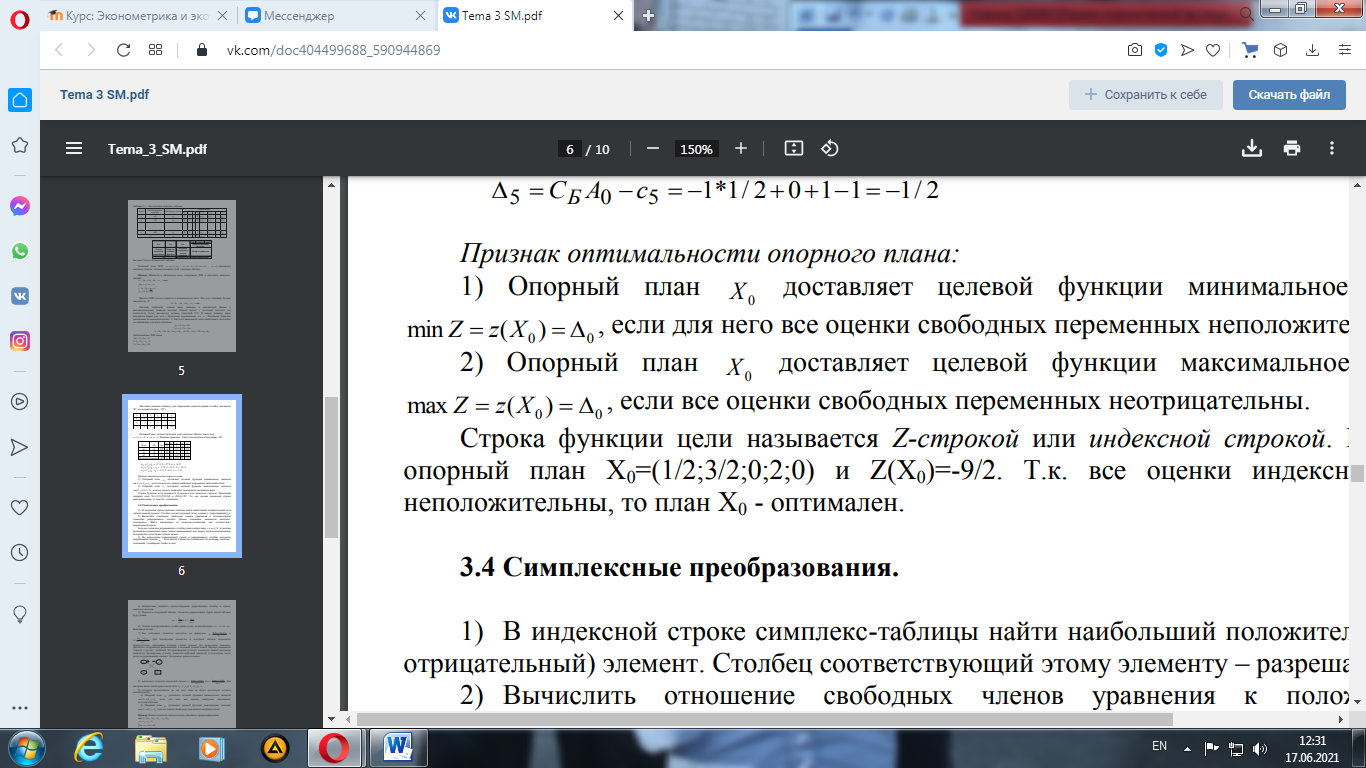
Признак оптимальности опорного плана: 1) Опорный план X0 доставляет целевой функции минимальное значение 2) Опорный план X0 доставляет целевой функции максимальное значение Строка функции цели называется Z-строкой или индексной строкой. Начальный опорный план Х0=(1/2;3/2;0;2;0) и Z(Х0)= –9/2. Т.к. все оценки индексной строки неположительны, то план Х0 - оптимален. 12. Симплексные преобразования. 1) В индексной строке симплекс-таблицы найти наибольший положительный (или отрицательный) элемент. Столбец соответствующий этому элементу – разрешающий (j0). 2) Вычислить отношение свободных членов уравнения к положительным элементам разрешающего столбца. Данное отношение называется симплексотношением. Найти наименьшее из симплекс-отношений, оно соответствует разрешающей строке. Если все элементы разрешающего столбца jo неположительны, т.е. aijo≤ 0, то целевая функция не ограниченна снизу (задача минимизации) или сверху (задача максимизации) на множестве допустимых планов задачи. 3) На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент ai0j0. Если имеется несколько одинаковых по величине симплекс отношений, то выбирают любое из них.
4) Неизвестные элементы, соответствующие разрешающим столбцу и строке, меняются местами. 5) Переход к следующей таблице. Элементы разрешающей строки новой таблицы будут равны
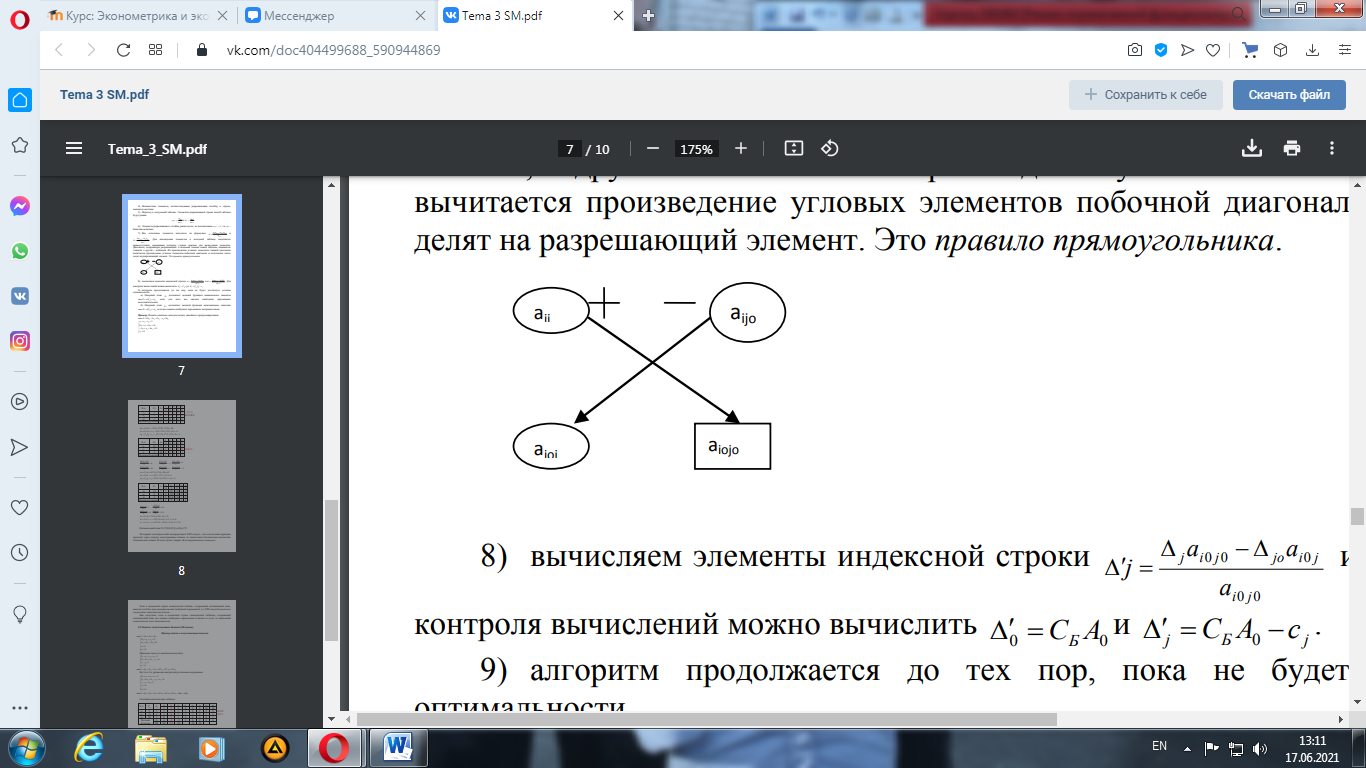
6) Элементы разрешающего столбца равны нулю, за исключением 7) Все остальные элементы находятся по формулам
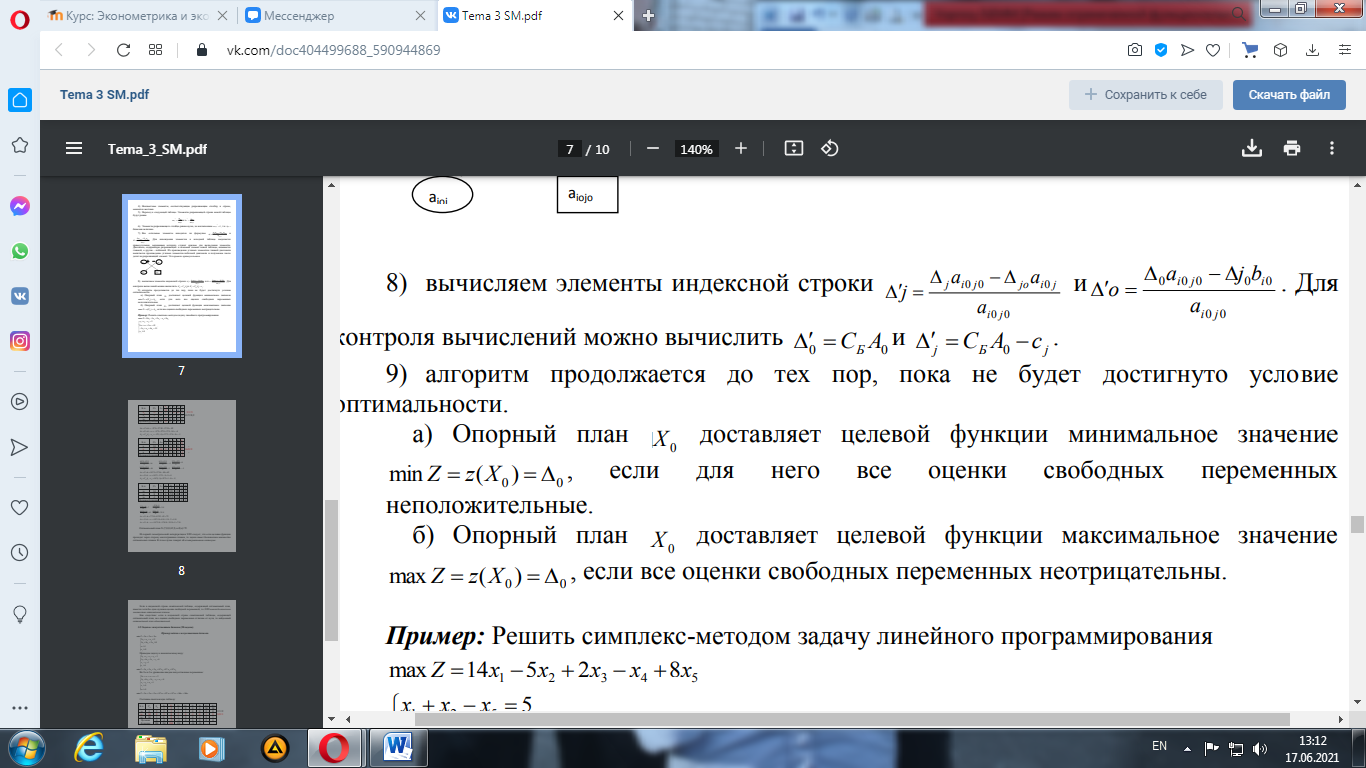
8) вычисляем элементы индексной строки
Для контроля вычислений можно вычислить 9) алгоритм продолжается до тех пор, пока не будет достигнуто условие оптимальности. а) Опорный план X0 доставляет целевой функции минимальное значение б) Опорный план X0 доставляет целевой функции максимальное значение Из первой геометрической интерпретации ЗЛП следует, что если целевая функция проходит через сторону многогранника планов, то задача имеет бесконечное множество оптимальных планов. В этом случае говорят об альтернативном оптимуме. Если в индексной строке симплексной таблице, содержащей оптимальный план, имеется хотя бы одна нулевая оценка свободной переменной, то ЗЛП имеет бесконечное множество оптимальных планов. Как следствие: если в индексной строке симплексной таблицы, содержащей оптимальный план, все оценки свободных переменных отличны от 0, то найденный оптимальный план единственный. Понятие двойственности. Двойственная задача - это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой задачи. Рассмотрим практическую ситуацию, которая приводит к необходимости рассмотрения двойственной задачи.
Предположим, что при изучении вопроса об использовании отходов основного производства на предприятии появилась возможность реализации их некоторой организации. Необходимо установить цены на эти отходы. Обозначим их как y1, y2... ym. Оценки должны быть установлены исходя из следующих требований, отражающие несовпадающие интересы предприятия и организации: 1) общую стоимость отходов производства покупающая организация стремиться минимизировать; 2) предприятие согласно уступить ресурсы только по таким ценам, при которых оно получит за них выручку не меньшую той, что могло бы получить, организовав собственное производство.
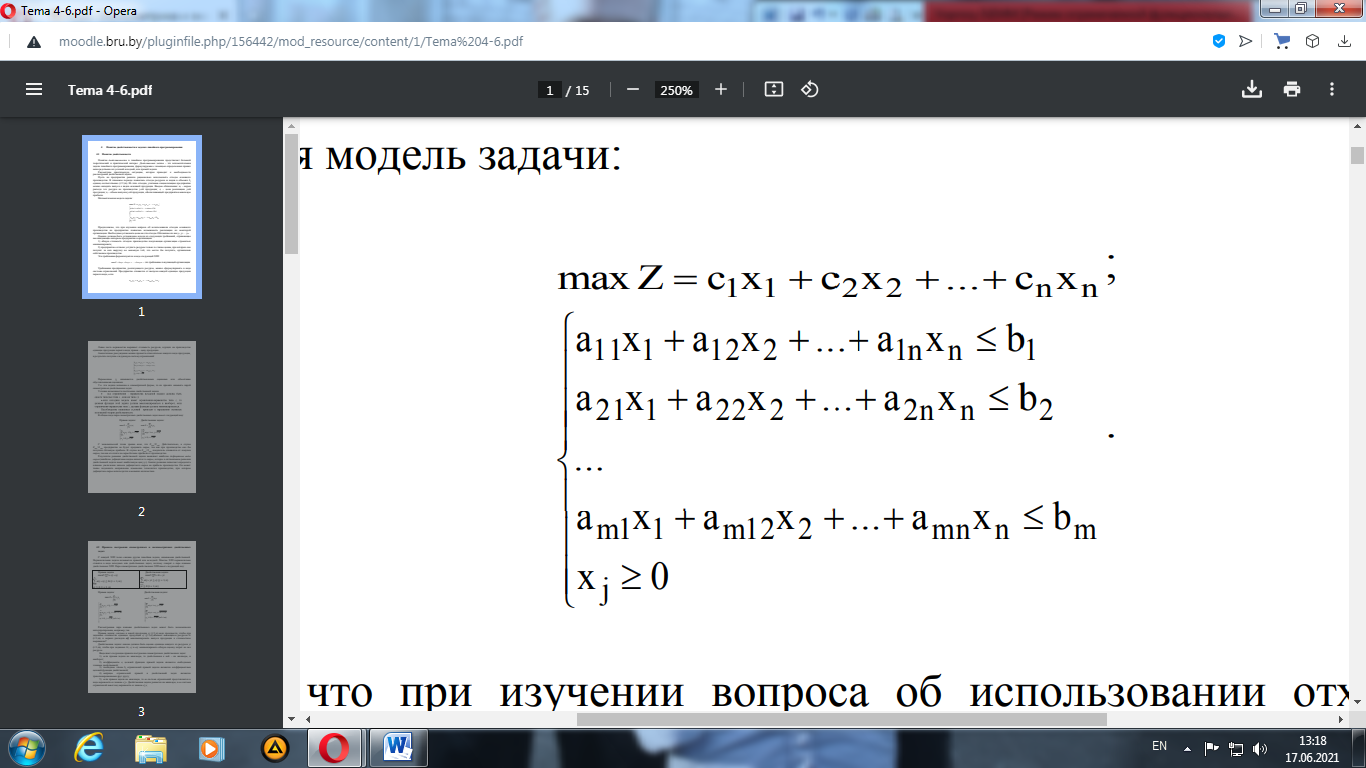
Эти требования формализуются в виде следующей ЗЛП:
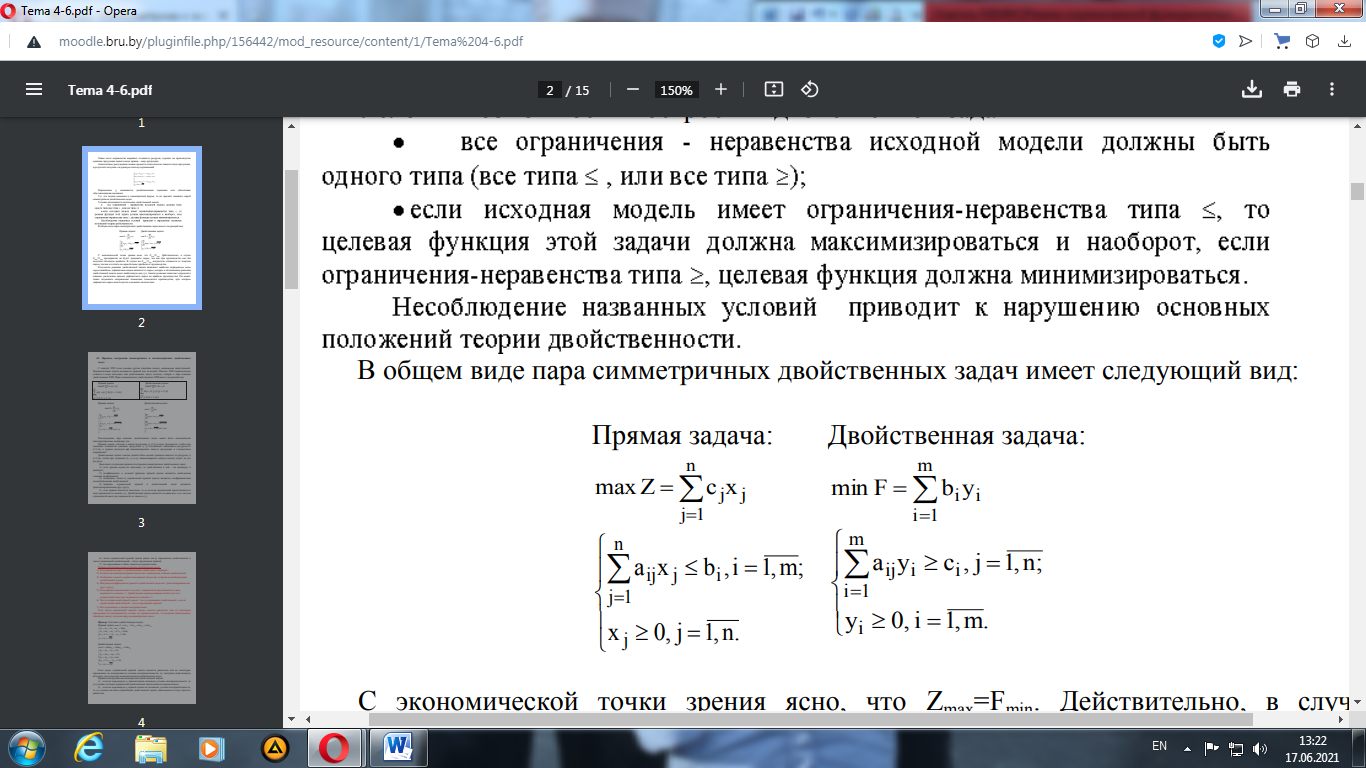
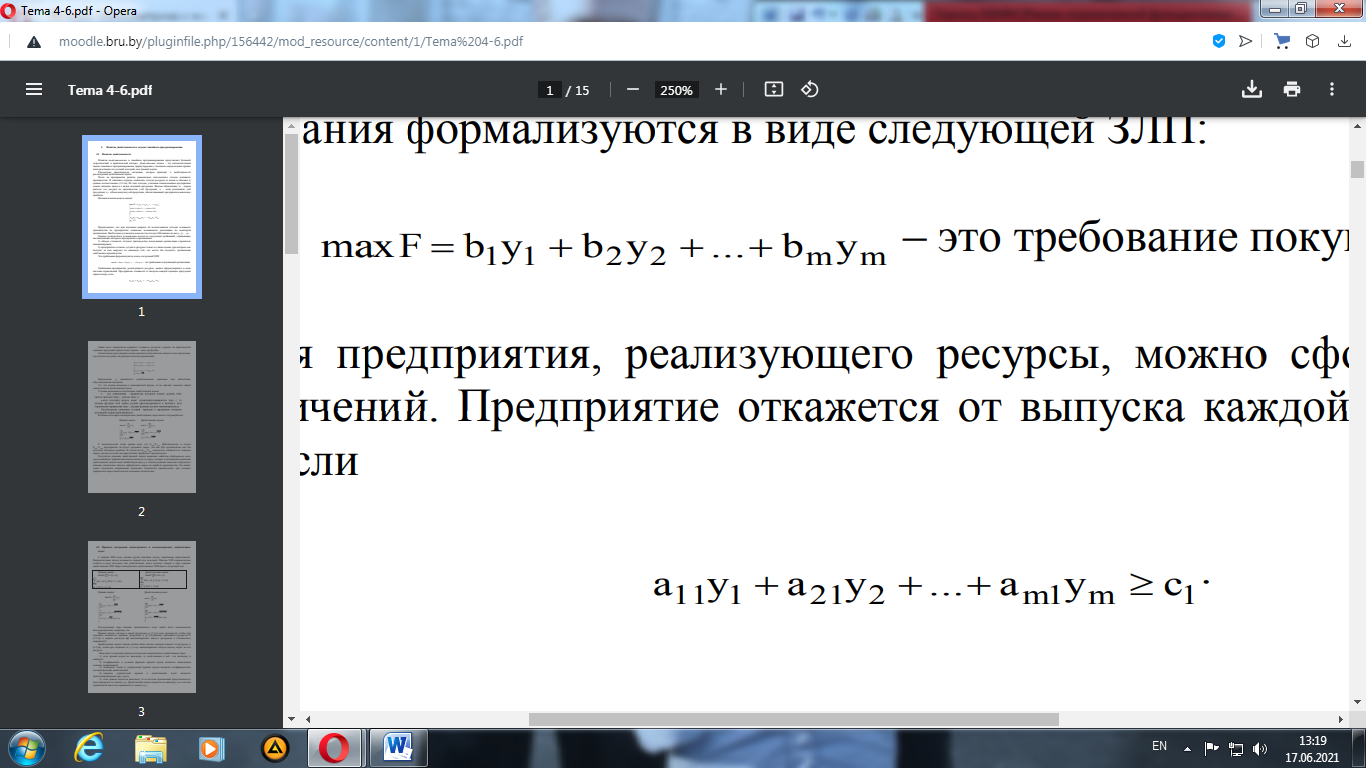
Требования предприятия, реализующего ресурсы, можно сформулировать в виде системы ограничений. Предприятие откажется от выпуска каждой единицы продукции первого вида, если Левая часть неравенства выражает стоимость ресурсов, идущих на производство единицы продукции первого вида; правая – цену продукции. Аналогичные рассуждения можно провести относительно каждого вида продукции, в результате получим следующую систему ограничений:
Переменные yi называются двойственными оценками. Т.к. эти задачи записаны в симметричной форме, то их принято называть парой симметричных двойственных задач. Условия возможности построения двойственной задачи:
|
||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.111.125 (0.021 с.) |
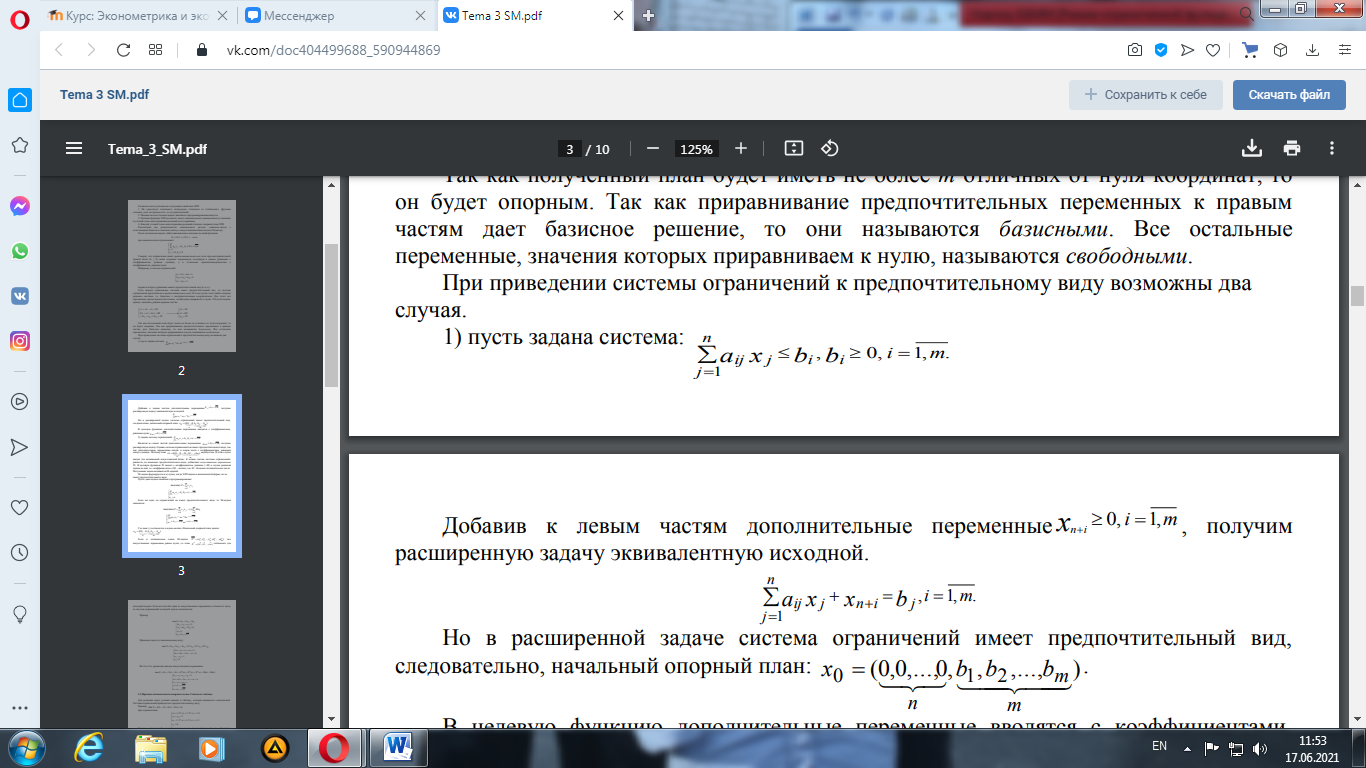
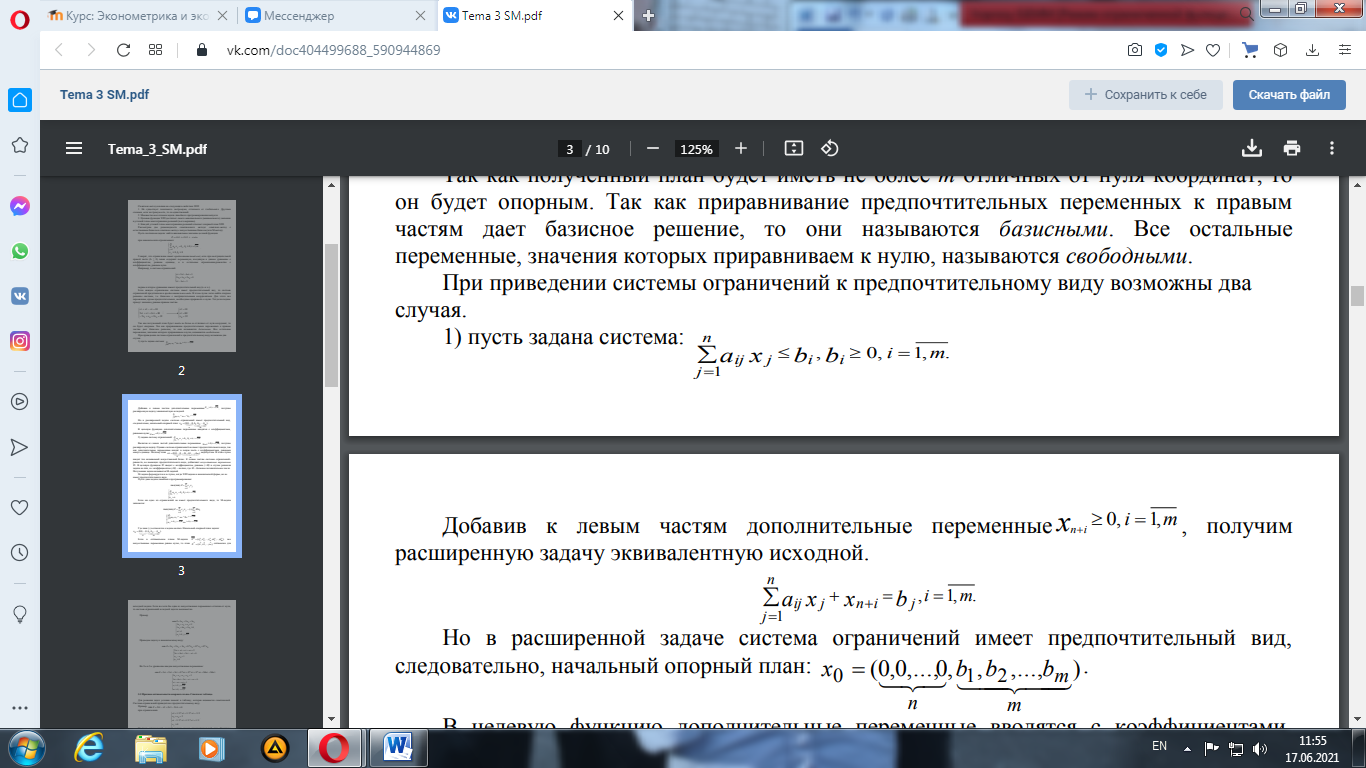 получим расширенную задачу, эквивалентную исходной.
получим расширенную задачу, эквивалентную исходной.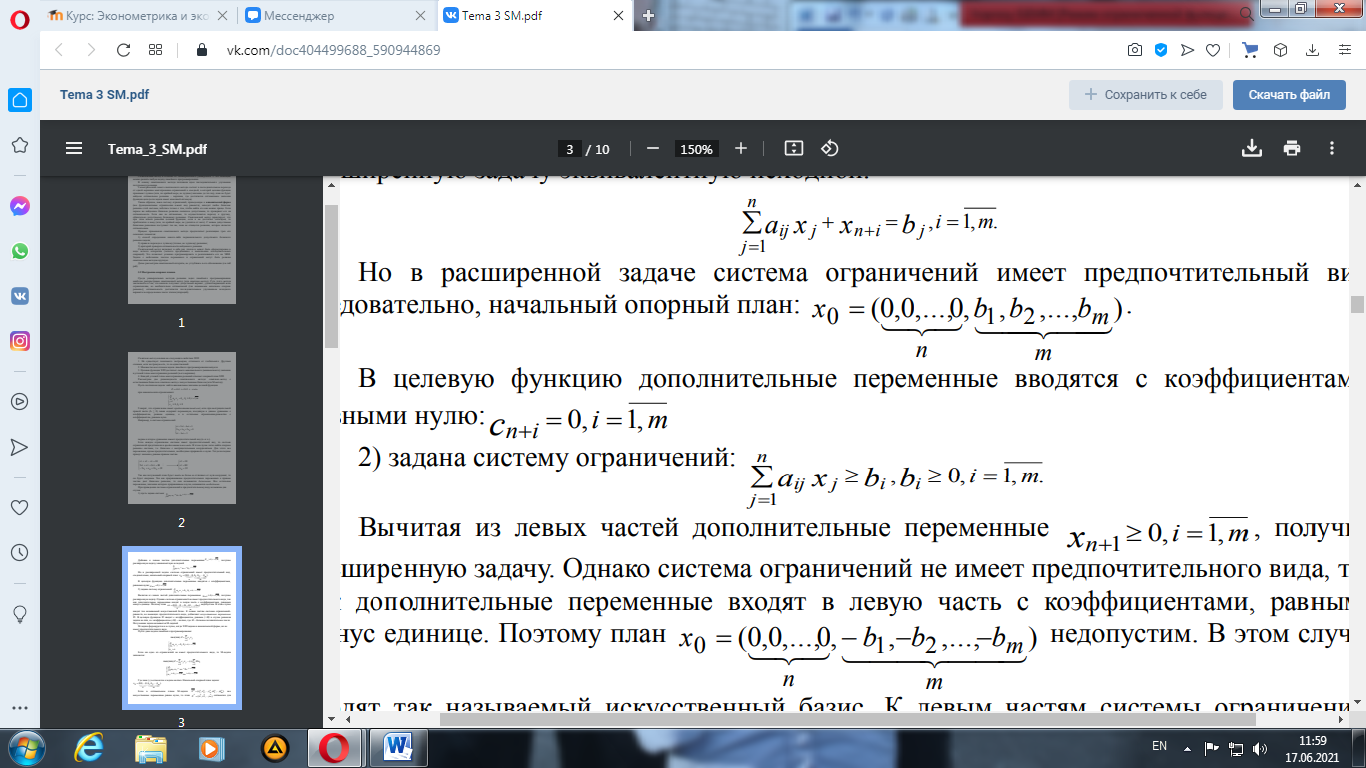
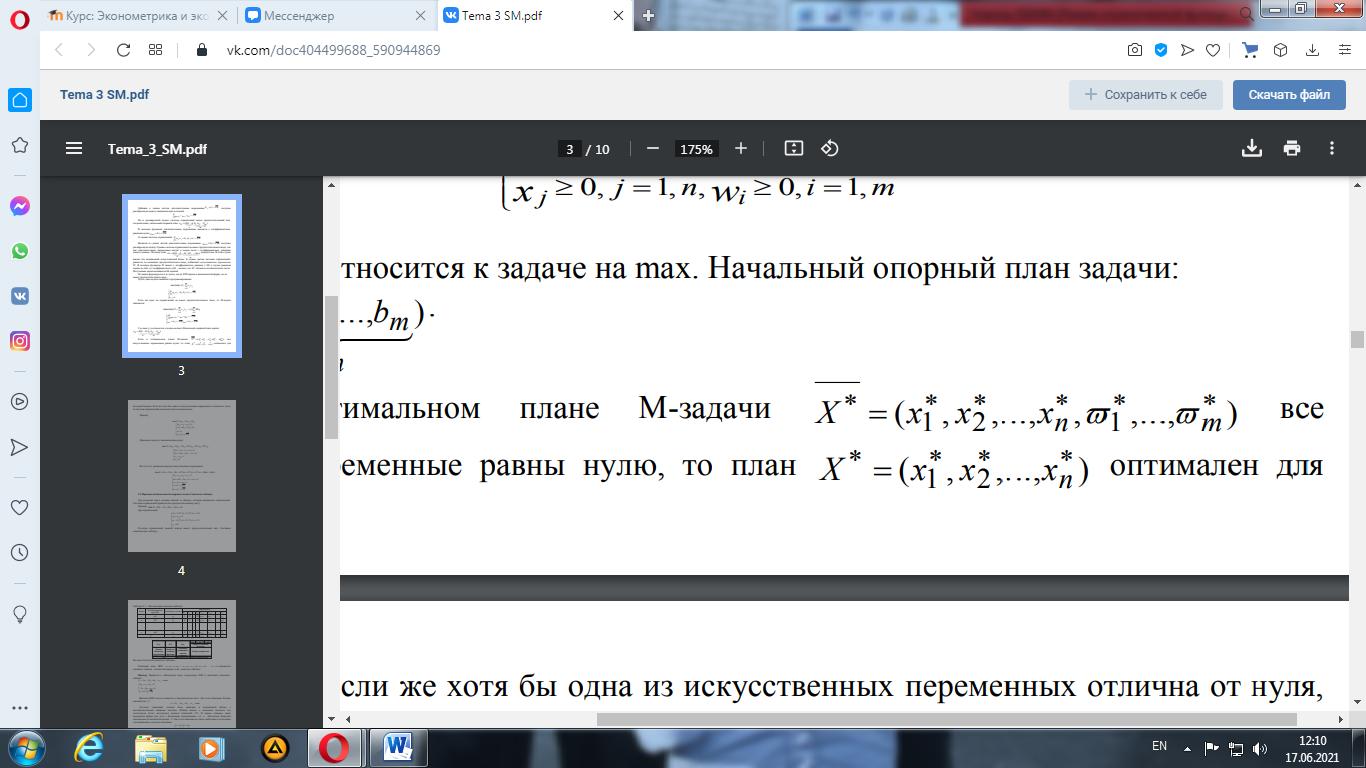 все искусственные переменные равны нулю, то план
все искусственные переменные равны нулю, то план 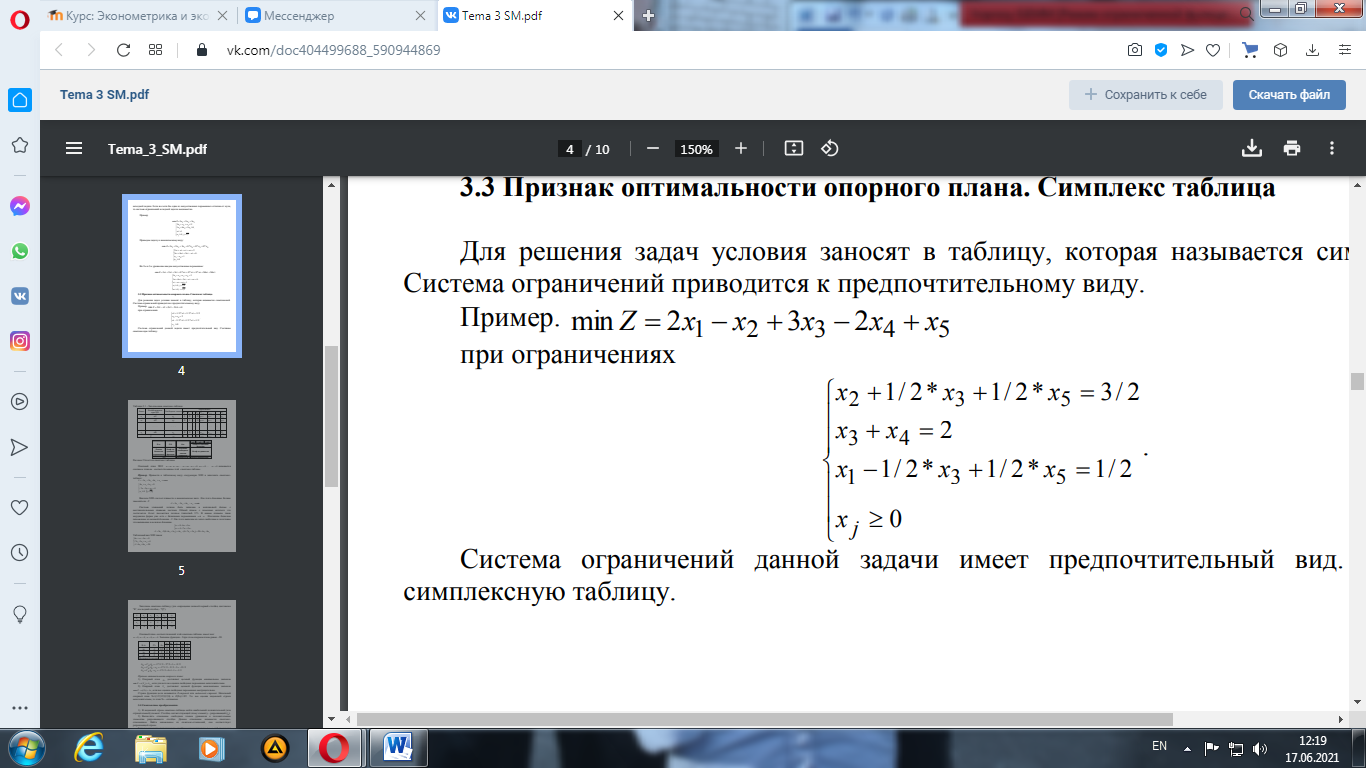
 , если для него все оценки свободных переменных неположительны.
, если для него все оценки свободных переменных неположительны.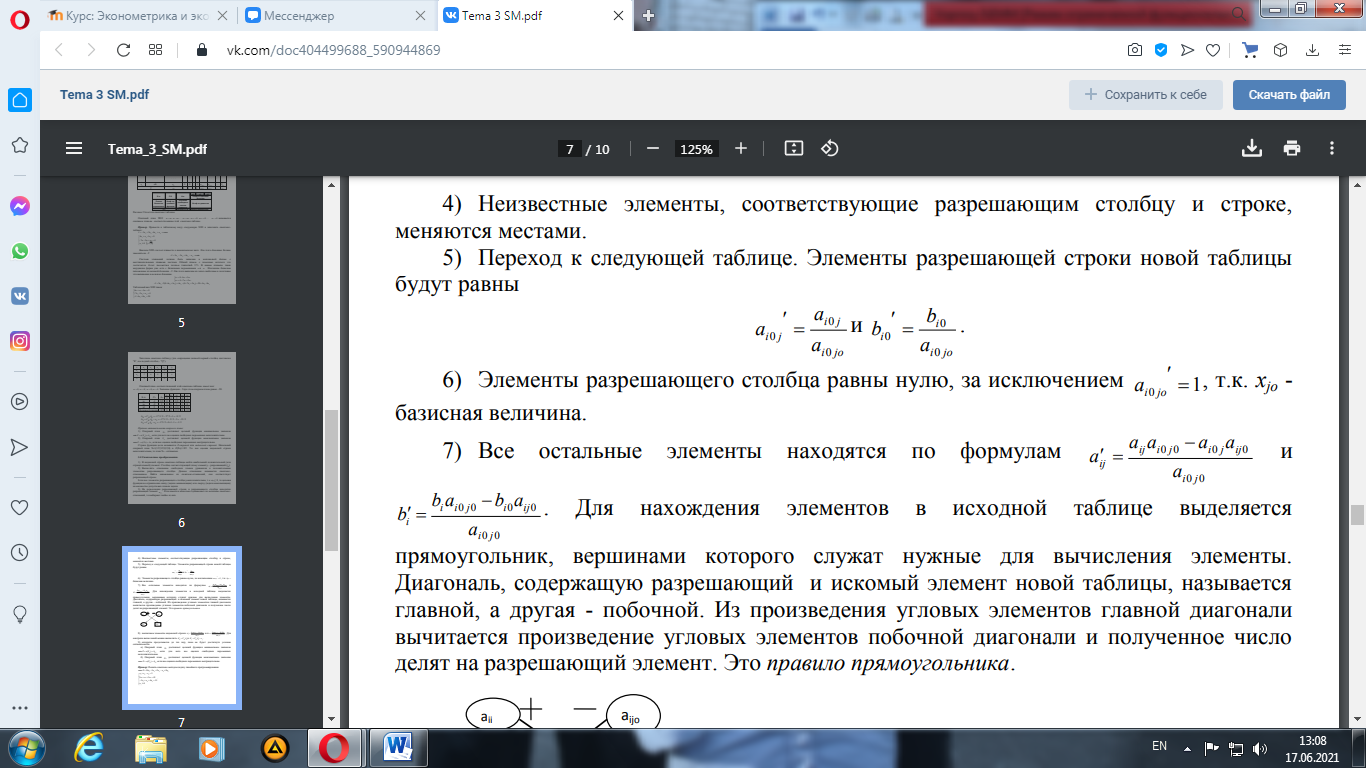
 – это требование покупающей организации.
– это требование покупающей организации.