
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
V Исследовать на полноту систему
Вновь заполним критериальную таблицу. Очевидно,
и А – полная система функций.
v Исследовать на полноту систему и в случае ее полноты выделить базисы
Прежде чем исследовать ее на полноту, преобразуем вторую функцию:
Теперь составим критериальную таблицу, из которой видно, что система является полной, а значит, из нее можно выделить базисы.
Общая методика выделения базисов из полной системы Для получения базисов составим КНФ, формируя дизъюнктивные одночлены из функций, которым соответствуют «минусы» в каждом столбце, преобразуем ее в ДНФ и упростим:
Полученная ДНФ содержит в себе в качестве конъюнктивных одночленов базисы исходной системы:
Анализируя критериальную таблицу можно убедиться в правильности найденных базисов системы. [2]
v Исследовать на полноту систему и в случае ее полноты выделить базисы
Составим критериальную таблицу, из которой видно, что система является полной.
Для выделения базисов составим КНФ по минусам и упростим:
Полученная ДНФ содержит одну функцию, следовательно, исходная система имеет единственный базис Примеры подсчета числа булевых функций v Найти число булевых функций, входящих в множество
При решении задачи необходимо учесть, что все булевы функции по своим значениям в нулевых и единичных наборах аргументов бывают четырех типов:
Из таблицы видно, что половина всех функций сохраняет каждую из констант, сразу обе константы сохраняет только одна функция. Тогда по формуле включений – исключений получим:
v Найти число булевых функций, входящих в множество
При решении любой задачи пересечения множеств необходимо рассматривать самый малочисленный класс, участвующий в выражении, в данном случае это класс L. Из четырех типов линейных функций, рассмотренных выше, только два сохраняют константу 0, поэтому ответом будет половина от всех линейных
v Найти число булевых функций, входящих в множество
При решении задачи необходимо учесть, что самодвойственные функции по своим значениям при нулевых и единичных наборах аргументов бывают двух типов:
Исходя из приведенной таблицы заметим, что
то есть самодвойственная функция либо сохраняет сразу обе константы, либо не сохраняет ни одной из них.
v Найти число булевых функций, входящих в множество
Для решения задачи используем закон дистрибутивности, а далее – формулу включений – исключений:
Заметим, что мощность вычитаемого пересечения трех классов опять рассчитывается от класса
v Найти число булевых функций, входящих в множество
Для решения задачи необходимо помнить, что мощность разности двух множеств B и C равна Тогда
v Найти число булевых функций, входящих в множество
v Найти число булевых функций, входящих в множество
Заметим, что данную задачу можно было решить устно. Как было сказано выше, самодвойственные функции, сохраняющие константу 0, сохраняют и константу 1. Поэтому, вычитая из самодвойственных, сохраняющих константу 0, линейные или сохраняющие константу 1, получим 0.
v Найти число булевых функций, входящих в множество
Заметим, что вычитание из множества
Тогда
v Найти число булевых функций, входящих в множество
3.4. Практические задания
3.4.1. Булевы функции: преобразования, двойственные, Нормальные формы
Задание 1. Упростить следующие формулы: а. б. в. г. д. е.
Задание 2. Выяснить, является ли функция g двойственной к функции f (д, е – используя принцип двойственности). а. б. в. г. д. е.
Задание 3. Указать все фиктивные переменные у функции f: [2] а. б. в. г. д. е.
Задание 4. Представить в СДНФ следующие функции: а. б. в. г. Задание 5. Представить в СКНФ следующие функции: а. б. в. г.
Задание 6. Построить ДНФ функций: а. б. в. г. Задание 7. Построить КНФ функций: а. б. в. г.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.89.24 (0.037 с.) |
 .
.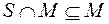 и
и 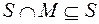 , при этом f (0,..., 0) = 0, f (1,..., 1) = 1, значит
, при этом f (0,..., 0) = 0, f (1,..., 1) = 1, значит  и
и  . Чтобы показать, что функции
. Чтобы показать, что функции  нелинейны, достаточно найти одну функцию, которая принадлежит
нелинейны, достаточно найти одну функцию, которая принадлежит  и не принадлежит
и не принадлежит  . Возьмем
. Возьмем  , удовлетворяющую требуемым условиям. Если
, удовлетворяющую требуемым условиям. Если  , то найдем функцию
, то найдем функцию 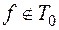 :
:  , а также функцию
, а также функцию 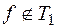 :
:  , причем обе эти функции несамодвойственны. Следовательно, критериальная таблица имеет вид
, причем обе эти функции несамодвойственны. Следовательно, критериальная таблица имеет вид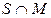
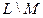
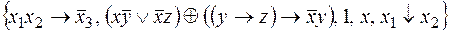 ,
,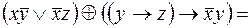
 .
.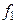
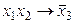
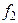

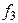
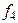

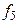
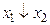
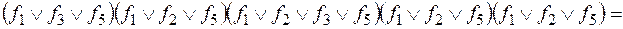
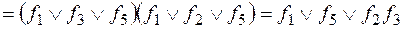 .
.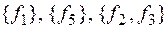 .
. .
.
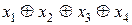


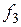
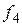

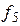



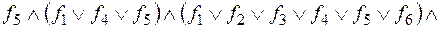
 .
.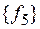 .
. .
. .
.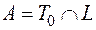 .
.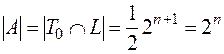 .
.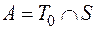 .
.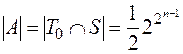 .
. =
=  =
=  ,
,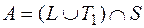 .
. .
.
 .
.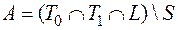 .
.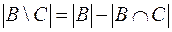 .
.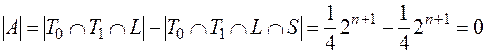 .
.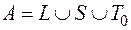 .
.
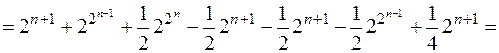
 .
. .
.


 .
. .
.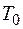 ряда других множеств равносильно вычитанию их объединения:
ряда других множеств равносильно вычитанию их объединения: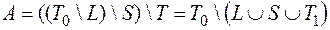 .
.
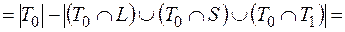


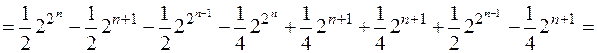
 .
. .
.
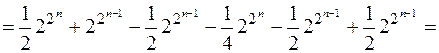
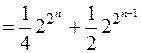 .
.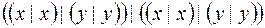 ;
;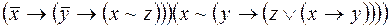 ;
;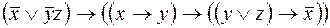 ;
;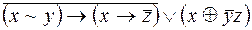 ;
;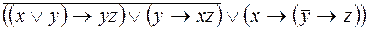 ;
;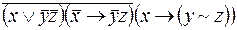 .
. ;
;  .
.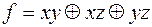 ;
;  .
. ;
; 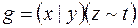 .
.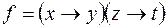 ;
; 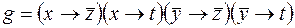 .
. ;
;  .
. ;
;  .
.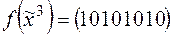 .
. .
. .
. .
. .
.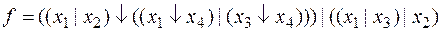 .
. .
. .
. .
.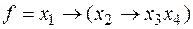 .
. .
. .
. .
. .
. .
.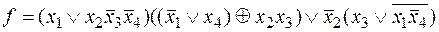 .
.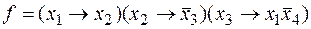 .
. .
.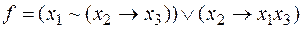 .
. .
.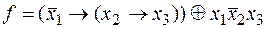 .
.


