
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычесление определителей четвертого порядкаСтр 1 из 2Следующая ⇒
ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОГО ЗАДАНИЯ ПО МОДУЛЮ «ЛИНЕЙНАЯ АЛГЕБРА» А. 1) Дать определение определителя 2 –го порядка
2) Записать правило вычисления определителя 3 - го порядка. Определитель 3 – го порядка вычисляется по правилу треугольников (или Саррюса), которое символически можно записать так:
(основания (основания равнобедрен- треугольников ных треуголь- параллельны ников вспомагательной параллельны диагонали) главной диагонали)
3) Вычислить определитель четвертого порядка разложением по элементам ряда.
Вычитаем из четвертой строки третью, получаем:
В четвертой строке только один элемент отличается от нуля. Раскрываем определитель по элементам четвертой строки.
Б. 1) Что называется матрицей? Матрицей называется прямоугольная таблица чисел, переменных, функций содержащая Размер матрицы записывают 2) Какие действия можно выполнять с матрицами? Сложение, умножение на число, произведение матриц, транспонирование. 3) Выполнить действия над матрицами. Найти
В. 1) Что называется рангом матрицы? Рангом матрицы называется наивысший порядок отличных от нуля миноров. Наивысшим порядком минора неравный нулю называется рангом матрицы 2) Свойства ранга матрицы. а) При транспортировании матрицы ее ранг не меняется; б) Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не меняется; в) Ранг матрицы не изменится при элементарных преобразованиях матрицы; 3)Определить ранг матрицы
Пользуясь способом окаймления миноров, найдем:
Вычисляем окаймляющий его минор:
Порядок последнего из найденных ненулевых миноров равен шагу матрицы. Следовательно, ранг матрицы равен двум. Г. 1) Каждая ли матрица имеет обратную? Всякая невырожденная матрица имеет обратную.
2) Как осуществляется проверка нахождения обратной матрицы В результате умножения заданной матрицы на обратную должна получаться единичная матрица. 3) Найти обратную матрицу
Найдем Вычисляем значения всех алгебраических дополнений элементов заданной матрицы.
В результате получаем: Поэтому обратная матрица будет:
Проверка:
Д. 1) Записать в чем заключается метод Гаусса? Метод Гаусса заключается в последовательном исключении неизвестных. 2) Какая система называется совместной? Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. 3)Решить систему уравнений: 1. Методом Гаусса; 2 Матричным методом.
Если в каком либо уравнении системы коэффициент при Перепишем систему, переставив местами первое и второе уравнение.
Исключив из второго уравнения
Разделим второе уравнение на
Аналогично исключим
Рассмотренным выше методом можно решать системы линейных алгебраических уравнений любого порядка. Однако с возростанием количества уравнений возрастает и трудность вычислительного алгоритма. Поэтому в случае систем высокого порядка необходимо использовать ЭВМ. 4) Решить систему матричным методом Данную систему уравнений запишем в матричной форме
Найдем
Исследовать систему на совместимость:
Составляем матрицу
Е. 1) Сформулировать теорему Кронекера – Капели. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы. 2) В каком случае система имеет единственное решение? Если ранг основной матрицы равен числу неизвестных, то система имеет единственное решение. 3) Исследовать систему на совместимость
Составляем матрицу
Вычислим ранг 1. Вторую и третью строки умножим на 2.Получим:
2. Из второй строки вычтем первую и к третьей строке прибавим первую строку, умноженную на -5. Получим:
3. Умножим третью строку на
Отсюда Проделав точно такие преобразования над матрицей
Отсюда, ясно, Решая эту (например, по формулам Крамера), находим
Далее использовав
1) Что называется собственным вектором матрицы Всякий ненулевой вектор
(характеристическим числом) 2) Найти собственные значения и собственные вектора матрицы: Составим характеристическое уравнение матрицы
Корни этого уравнения Для отыскания собственных векторов используем систему уравнений
Полагая Таким образом, собственному значению Если
Семейство собственных векторов соответствует этому собственному значению, определяется равенством
3. ВАРИАНТЫ КОНТРОЛЬНОГО ЗАДАНИЯ Нахождение ранга матрицы 1) Что называется рангом матрицы 2) Какие существуют методы нахождения ранга матрицы 3) Определить ранг матрицы 1.
4.
7. 10. 13.
16.
19. 21. 24. 27. 30.
3.4. Нахождение обратной матрицы 1. Написать схему нахождения обратной матрицы 2. Дать определение вырожденной матрицы 3. Найти обратную матрицу 1.
3. 5. 7.
9. 11. 13.
15. 17. 19. 21. 23. 25. 27. 29.
Библиографический список 1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры / Д.В. Беклемишев. – М.: Наука, 1984. – 328 с. 2. Ефимов Н.В. Квадратичные формы и матрицы / Н.В. Ефимов. – М.: Наука, 1975. – 227 с. 3. Клетеник Д.В. Сборник задач по аналитической геометрии / Д.В. Клетеник. М.: Наука, 1980. – 239 с. 4. Данко П.Е Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я.Кожевникова. – М.: Высшая школа, 2003. – 303 с.- Ч.I. 5. Данко П.Е Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я.Кожевникова. – М.: Высшая школа, 2003. – 417 с., Ч.II.
6. Бугров Я.С. Высшая математика Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1984. – 175 с. 7. Борисович З.И. Определители и матрицы / З.И. Борисович – М.: Наука, 1988. – 184 с. 8. Щипачов В.С. Курс высшей математики / В.С. Щипачов. – 2 изд. пере раб. – М.: Проспект, 2002. – 599 с. 9. Канатников А.Н. Линейная алгебра для студентов ВТУзов / А.Н. Канатников. – Изд-во МГТУ им. Н.Э. Баумана, 2001. – 336 с.
ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОГО ЗАДАНИЯ ПО МОДУЛЮ «ЛИНЕЙНАЯ АЛГЕБРА» А. 1) Дать определение определителя 2 –го порядка
2) Записать правило вычисления определителя 3 - го порядка. Определитель 3 – го порядка вычисляется по правилу треугольников (или Саррюса), которое символически можно записать так:
(основания (основания равнобедрен- треугольников ных треуголь- параллельны ников вспомагательной параллельны диагонали) главной диагонали)
3) Вычислить определитель четвертого порядка разложением по элементам ряда.
Вычитаем из четвертой строки третью, получаем:
В четвертой строке только один элемент отличается от нуля. Раскрываем определитель по элементам четвертой строки.
Б. 1) Что называется матрицей? Матрицей называется прямоугольная таблица чисел, переменных, функций содержащая Размер матрицы записывают 2) Какие действия можно выполнять с матрицами? Сложение, умножение на число, произведение матриц, транспонирование. 3) Выполнить действия над матрицами. Найти
В. 1) Что называется рангом матрицы? Рангом матрицы называется наивысший порядок отличных от нуля миноров. Наивысшим порядком минора неравный нулю называется рангом матрицы 2) Свойства ранга матрицы. а) При транспортировании матрицы ее ранг не меняется; б) Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не меняется; в) Ранг матрицы не изменится при элементарных преобразованиях матрицы; 3)Определить ранг матрицы
Пользуясь способом окаймления миноров, найдем:
Вычисляем окаймляющий его минор:
Порядок последнего из найденных ненулевых миноров равен шагу матрицы. Следовательно, ранг матрицы равен двум.
Г. 1) Каждая ли матрица имеет обратную? Всякая невырожденная матрица имеет обратную.
2) Как осуществляется проверка нахождения обратной матрицы В результате умножения заданной матрицы на обратную должна получаться единичная матрица. 3) Найти обратную матрицу
Найдем Вычисляем значения всех алгебраических дополнений элементов заданной матрицы.
В результате получаем: Поэтому обратная матрица будет:
Проверка:
Д. 1) Записать в чем заключается метод Гаусса? Метод Гаусса заключается в последовательном исключении неизвестных. 2) Какая система называется совместной? Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. 3)Решить систему уравнений: 1. Методом Гаусса; 2 Матричным методом.
Если в каком либо уравнении системы коэффициент при Перепишем систему, переставив местами первое и второе уравнение.
Исключив из второго уравнения
Разделим второе уравнение на
Аналогично исключим
Рассмотренным выше методом можно решать системы линейных алгебраических уравнений любого порядка. Однако с возростанием количества уравнений возрастает и трудность вычислительного алгоритма. Поэтому в случае систем высокого порядка необходимо использовать ЭВМ. 4) Решить систему матричным методом Данную систему уравнений запишем в матричной форме
Найдем
Исследовать систему на совместимость:
Составляем матрицу
Е. 1) Сформулировать теорему Кронекера – Капели. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы. 2) В каком случае система имеет единственное решение? Если ранг основной матрицы равен числу неизвестных, то система имеет единственное решение. 3) Исследовать систему на совместимость
Составляем матрицу
Вычислим ранг 1. Вторую и третью строки умножим на 2.Получим:
2. Из второй строки вычтем первую и к третьей строке прибавим первую строку, умноженную на -5. Получим:
3. Умножим третью строку на
Отсюда Проделав точно такие преобразования над матрицей
Отсюда, ясно, Решая эту (например, по формулам Крамера), находим
Далее использовав
1) Что называется собственным вектором матрицы Всякий ненулевой вектор
(характеристическим числом) 2) Найти собственные значения и собственные вектора матрицы: Составим характеристическое уравнение матрицы
Корни этого уравнения Для отыскания собственных векторов используем систему уравнений
Полагая Таким образом, собственному значению Если
Семейство собственных векторов соответствует этому собственному значению, определяется равенством
3. ВАРИАНТЫ КОНТРОЛЬНОГО ЗАДАНИЯ Вычесление определителей четвертого порядка 1) Перечислить свойства определителя: 2) Вычислить определитель: 1. 2.
3.
4. 5.
11. 12.
13.
14. 15. 16.
,
23. 24. 25. 26.
|
|||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 47; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.67.177 (0.289 с.) |

 Определителем второго порядка называется число
Определителем второго порядка называется число 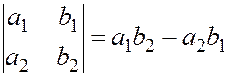 .
.











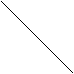
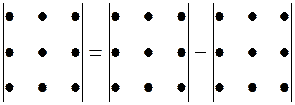
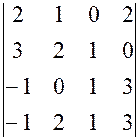 .
.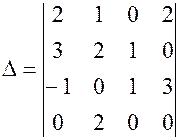 .
.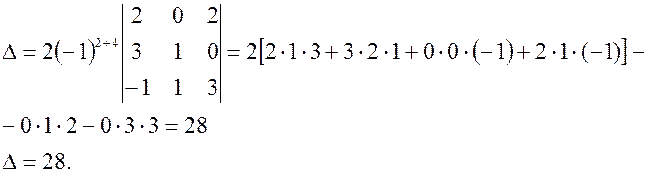
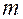 строк одинаковой длины и
строк одинаковой длины и 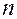 столбцов.
столбцов.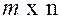 .
.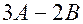 , если:
, если: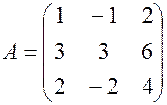
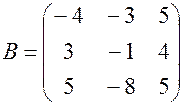 .
.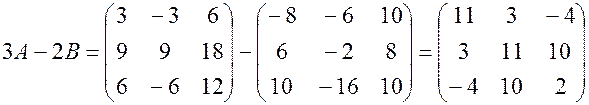 .
.



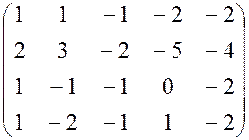 .
.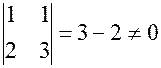 .
. .
. .
.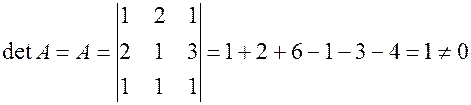 .
.
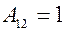
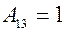

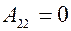
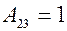


 .
.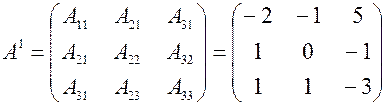 .
.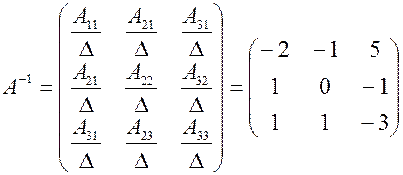 .
. .
.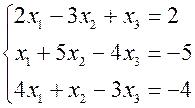 .
.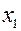 равен 1, то это уравнение лучше всего поставить первым.
равен 1, то это уравнение лучше всего поставить первым. .
.
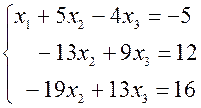 .
. .
.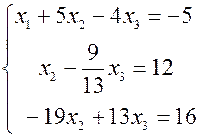 .
.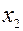 из третьего уравнения. Приходим к системе
из третьего уравнения. Приходим к системе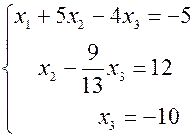 .
.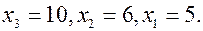
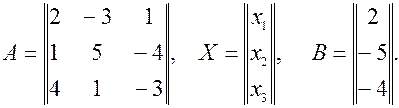
 матрицы
матрицы 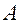 .
.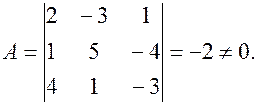
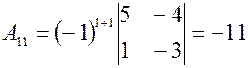
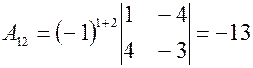
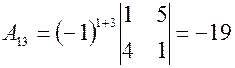

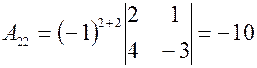
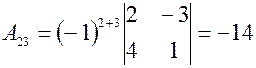
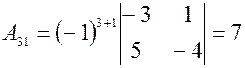
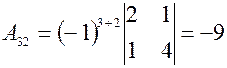
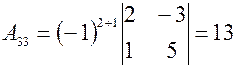
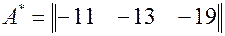
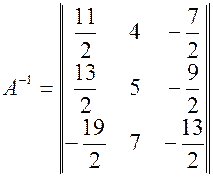



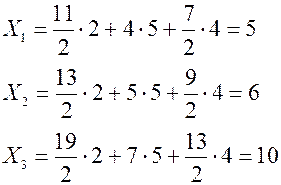
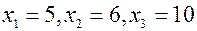 .
. .
.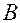 .
.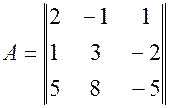
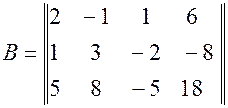 .
.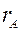 матрицы
матрицы 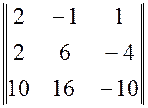 .
. .
. и затем из третьей строки вычтем вторую
и затем из третьей строки вычтем вторую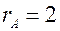 .
.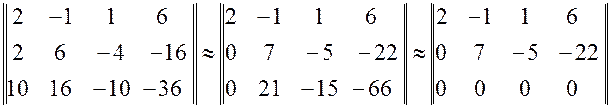 .
.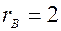 . Так как
. Так как  , то на основании теоремы Кронекера – Капели заключаем, что система совместна, так как число неизвестных 3 больше ранга 2. Для отыскания всех решений убираем нулевую строку матрицы, а оставшиеся два записываем в виде
, то на основании теоремы Кронекера – Капели заключаем, что система совместна, так как число неизвестных 3 больше ранга 2. Для отыскания всех решений убираем нулевую строку матрицы, а оставшиеся два записываем в виде  .
.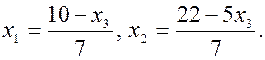
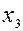 , определяем по формулам
, определяем по формулам 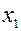 и
и 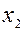 . Например, если
. Например, если 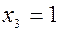 , то
, то  и
и 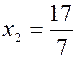 , если
, если 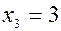 , то
, то  и
и 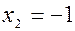 . Подставляя выражения для
. Подставляя выражения для  , удовлетворяющий условию
, удовлетворяющий условию называется собственным вектором преобразования матрицы
называется собственным вектором преобразования матрицы 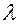 собственным значением
собственным значением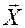 . Собственным значением
. Собственным значением 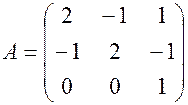
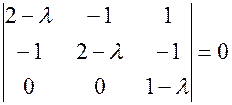
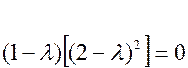
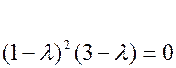
 .
.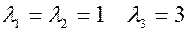 являются собственными значения линейного преобразования.
являются собственными значения линейного преобразования.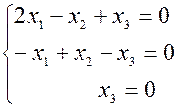 .
.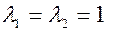 получаем систему.
получаем систему. .
. для определения координат собственного вектора получим систему
для определения координат собственного вектора получим систему .
. .
. , 2.
, 2.  , 3.
, 3. 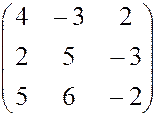 ,
,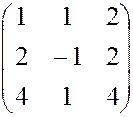 , 5.
, 5.  , 6.
, 6.  , 8.
, 8. 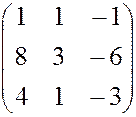 , 9.
, 9. 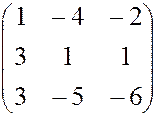 ,
,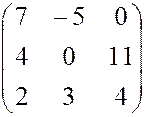 , 11.
, 11. 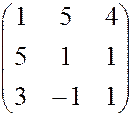 , 12.
, 12.  ,
, , 14.
, 14. 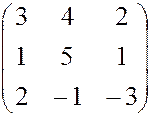 , 15.
, 15. 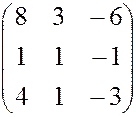 ,
, 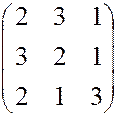 , 17.
, 17. 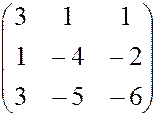 ,18
,18  , 20.
, 20. 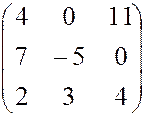 ,
, , 22.
, 22. 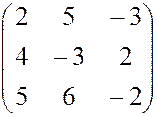 , 23.
, 23. 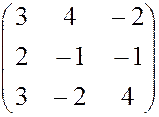 ,
,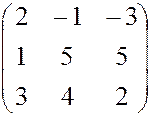 , 25.
, 25. 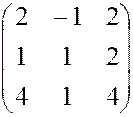 , 26.
, 26. 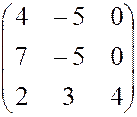 .
. , 28.
, 28.  , 29.
, 29. 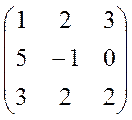 ,
,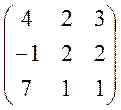 .
.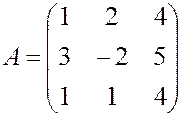 , 2.
, 2. 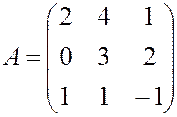 ,
, , 4.
, 4. 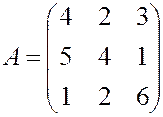 ,
, , 6.
, 6. 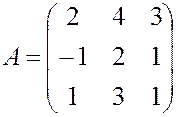 ,
,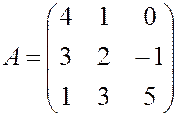 , 8.
, 8. 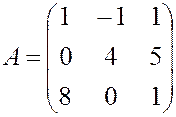 ,
,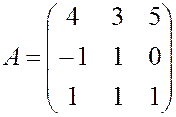 , 10.
, 10.  ,
,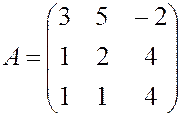 , 12.
, 12. 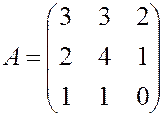 ,
, , 14.
, 14. 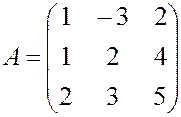 , 18.
, 18.  ,
, , 20.
, 20. 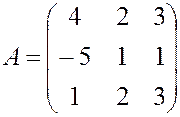 ,
,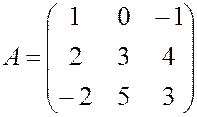 , 22.
, 22. 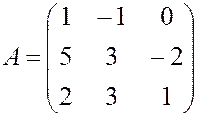 ,
,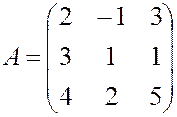 , 24.
, 24. 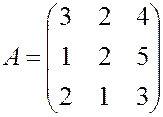 ,
,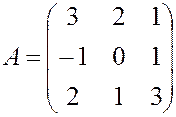 , 26.
, 26. 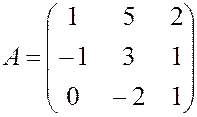 ,
,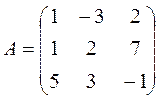 , 28.
, 28. 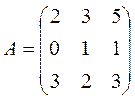 ,
,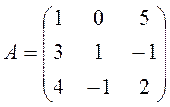 , 30.
, 30. 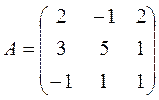 .
. , 6.
, 6. 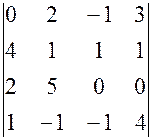 ,
,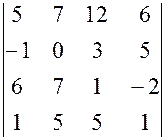 , 7.
, 7.  ,
,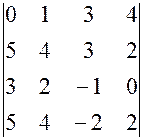 , 8.
, 8. 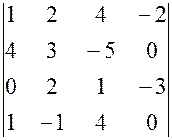 ,
, ,
,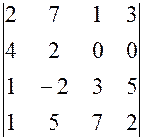 ,, 10.
,, 10. 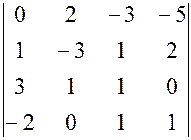 ,
,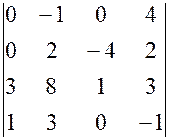 , 17.
, 17. 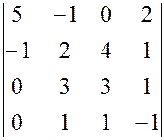 ,
, 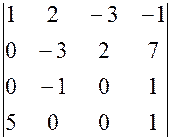 , 18.
, 18.  ,
,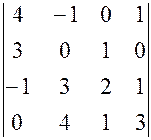 , 19.
, 19. 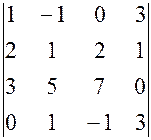 ,
,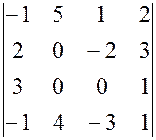 20.
20. 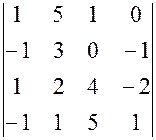 ,
, , 21.
, 21. 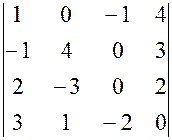 ,
,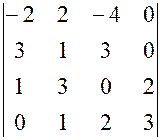 , 22.
, 22. 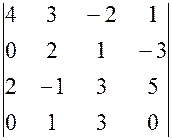 ,
,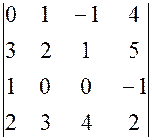 , 27.
, 27. 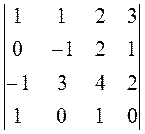 ,
,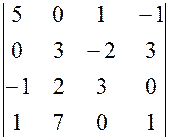 , 28.
, 28. 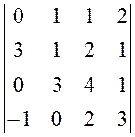 ,
, , 29.
, 29. 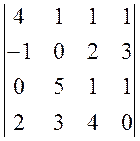 ,
, , 30.
, 30. 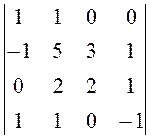 .
.


