Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Циркуляция векторного поля. Формула СтоксаСтр 1 из 4Следующая ⇒
ЗАНЯТИЕ № 8 ДИСТАНЦИОННОЕ ОБУЧЕНИЕ ЧАСТЬ А) РОТОР ВЕКТОРНОГО ПОЛЯ. ФОРМУЛА СТОКСА Ротор векторного поля Ротором векторного поля В результате разложения определителя по первой строке получим
Ротор является дифференциальным оператором первого порядка. Он обладает свойством линейности: Отметим, что в криволинейных координатах (например, в цилиндрических или сферических) формула для вычисления ротора имеет другой вид. Циркуляция векторного поля. Формула Стокса
Циркуляцией векторного поля
Направление обхода контура и выбор стороны поверхности согласованы следующим образом: если смотреть из конца нормали Формула Стокса является обобщением формулы Грина (см. п. 14.3) на пространственный случай. В координатной записи она имеет вид
Здесь ДИСТАНЦИОННОЕ ОБУЧЕНИЕ 16.4.1. Найти 16.4.2. Решить задачу 14.5.5 б) с помощью формулы Стокса. 16.4.3. Найти циркуляцию векторного поля 16.4.4. Вычислить циркуляцию вектора 16.4.5. Найти циркуляцию векторного поля 16.4.6. Вычислить циркуляцию векторного поля
Ответы. 16.4.1. а) ЧАСТЬ Б) ДТСТАНЦИОННОЕ ОБУЧЕНИЕ СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ Вычисление дифференциальных операций с помощью Оператора Гамильтона Градиентом скалярного поля Операцию нахождения градиента функции При вычислениях с участием оператора Гамильтона важно помнить, что, как любой дифференциальный оператор первого порядка, он обладает свойством линейности: При действии символа "набла" на произведение двух величин (скалярных или векторных), зависящих от координат, применяется правило производной произведения: ДИСТАНЦИОННОЕ ОБУЧЕНИЕ 17.5.1. Найти а) 17.5.2. Показать, что: а) б) в) 17.5.3. Пусть 17.5.4. Проверить потенциальность и найти потенциал поля 17.5.5. Проверить соленоидальность поля 17.5.6. Какую функцию
17.5.7. Найти векторный потенциал поля 17.5.8. Показать, что поле
Ответы. 17.5.1. а)
ЧАСТЬ В) ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (ОДУ) ПЕРВОГО ПОРЯДКА Основные понятия ДИСТАНЦИОННОЕ ОБУЧЕНИЕ 19.6.1. 19.6.3. Ответы. 19.6.1. 19.6.3.
ЗАНЯТИЕ № 8 ДИСТАНЦИОННОЕ ОБУЧЕНИЕ ЧАСТЬ А) РОТОР ВЕКТОРНОГО ПОЛЯ. ФОРМУЛА СТОКСА Ротор векторного поля Ротором векторного поля В результате разложения определителя по первой строке получим
Ротор является дифференциальным оператором первого порядка. Он обладает свойством линейности: Отметим, что в криволинейных координатах (например, в цилиндрических или сферических) формула для вычисления ротора имеет другой вид. Циркуляция векторного поля. Формула Стокса
Циркуляцией векторного поля
Направление обхода контура и выбор стороны поверхности согласованы следующим образом: если смотреть из конца нормали Формула Стокса является обобщением формулы Грина (см. п. 14.3) на пространственный случай. В координатной записи она имеет вид
Здесь
|
||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.043 с.) |
 называется векторная функция, которую в декартовых координатах определяют формулой
называется векторная функция, которую в декартовых координатах определяют формулой  .
.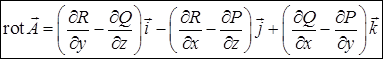 .
.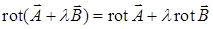 , где
, где  — числовая константа.
— числовая константа.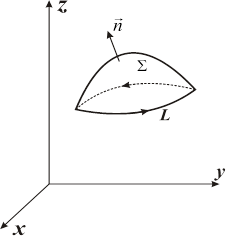
 по замкнутому контуру
по замкнутому контуру 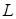 . Если поле
. Если поле 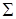 , ограниченную контуром
, ограниченную контуром  (формула Стокса).
(формула Стокса).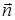 , то обход контура
, то обход контура 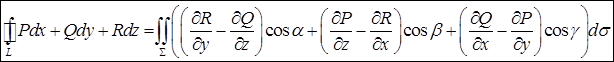 .
.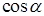 ,
,  ,
, 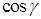 – координаты единичной нормали
– координаты единичной нормали 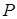 ,
, 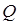 и
и 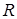 – компоненты векторного поля
– компоненты векторного поля 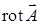 , если: а)
, если: а) 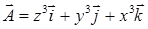 ; б)
; б) 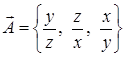 .
.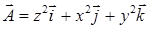 по сечению сферы
по сечению сферы 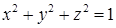 плоскостью
плоскостью 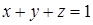 в положительном направлении обхода относительно вектора
в положительном направлении обхода относительно вектора 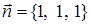 .
.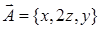 вдоль контура
вдоль контура 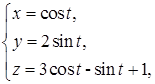 пробегаемого в направлении возрастания параметра
пробегаемого в направлении возрастания параметра 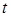 . Вычисления произвести непосредственно и по формуле Стокса.
. Вычисления произвести непосредственно и по формуле Стокса.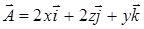 по ломаной
по ломаной 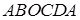 , где
, где 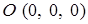 ,
, 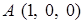 ,
, 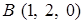 ,
, 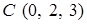 ,
, 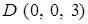 — вершины прямоугольного параллелепипеда. При вычислении по теореме Стокса в качестве поверхности, опирающейся на контур, выберите часть поверхности этого параллелепипеда.
— вершины прямоугольного параллелепипеда. При вычислении по теореме Стокса в качестве поверхности, опирающейся на контур, выберите часть поверхности этого параллелепипеда.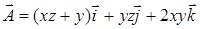 по контуру, вырезанному из двуполостного гиперболоида
по контуру, вырезанному из двуполостного гиперболоида 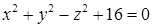 плоскостями
плоскостями 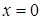 ,
, 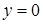 и
и 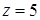 при
при 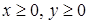 .
. ; б)
; б) 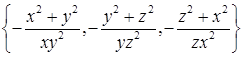 . 16.4.3.
. 16.4.3.  . 16.4.4.
. 16.4.4. 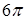 . 16.4.5.
. 16.4.5. 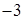 . 16.4.6.
. 16.4.6. 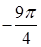 .
. называется вектор
называется вектор 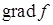 , координаты которого в декартовой системе определяются как частные производные функции
, координаты которого в декартовой системе определяются как частные производные функции  по соответствующим переменным:
по соответствующим переменным: 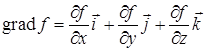 . Свойства градиента перечислены в [1], 21.1.2.
. Свойства градиента перечислены в [1], 21.1.2. можно представить при помощи т. н. оператора Гамильтона
можно представить при помощи т. н. оператора Гамильтона 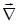 (этот символ читается набла):
(этот символ читается набла):  . Оператор Гамильтона является векторным дифференциальным оператором первого порядка, и он действует на функции, расположенные справа от него. Так, градиент можно записать в виде
. Оператор Гамильтона является векторным дифференциальным оператором первого порядка, и он действует на функции, расположенные справа от него. Так, градиент можно записать в виде 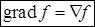 . Дивергенцию можно рассматривать как скалярное произведение символа "набла" и векторного поля
. Дивергенцию можно рассматривать как скалярное произведение символа "набла" и векторного поля 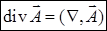 . Ротор можно представить как векторное произведение:
. Ротор можно представить как векторное произведение: 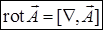 .
.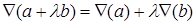 . Здесь
. Здесь  и
и 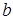 – выражения, зависящие от координат точки, а
– выражения, зависящие от координат точки, а 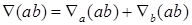 . Запись символа "набла" в виде
. Запись символа "набла" в виде 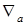 показывает, что оператор Гамильтона действует на сомножитель
показывает, что оператор Гамильтона действует на сомножитель 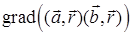 ; б)
; б)  ; в)
; в) 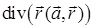 ; г)
; г) 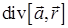 ; д)
; д) 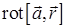 , где
, где 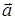 и
и 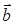 – постоянные векторы, а
– постоянные векторы, а 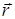 - радиус-вектор точки
- радиус-вектор точки 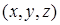 .
.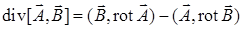 ;
; , где
, где 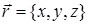 , а
, а 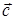 – постоянный вектор;
– постоянный вектор; .
.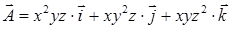 . Вычислить
. Вычислить 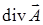 и
и  : а)
: а)  ; б)
; б) 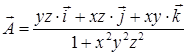 .
. 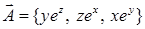 и найти его векторный потенциал.
и найти его векторный потенциал. следует взять в ответе к задаче 17.5.5, чтобы получить векторный потенциал
следует взять в ответе к задаче 17.5.5, чтобы получить векторный потенциал 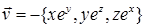 ?
?  .
. является гармоническим и найти его скалярный и векторный потенциалы.
является гармоническим и найти его скалярный и векторный потенциалы. ; б)
; б)  ; в)
; в) 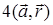 ; г) 0; д)
; г) 0; д)  . 17.5.3.
. 17.5.3.  ;
;  . 17.5.4. а)
. 17.5.4. а) 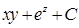 ; б)
; б)  . 17.5.5.
. 17.5.5.  . 17.5.6.
. 17.5.6. 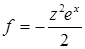 . 17.5.7.
. 17.5.7. 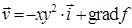 . 17.5.8.
. 17.5.8. 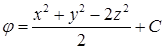 ;
; 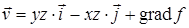 .
.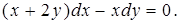 19.6.2.
19.6.2. 
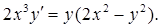 19.6.4.
19.6.4. 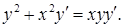 19.6.5.
19.6.5. 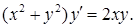 19.6.6.
19.6.6. 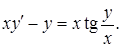
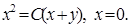 19.6.2.
19.6.2. 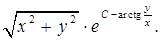
 19.6.4.
19.6.4.  19.6.5.
19.6.5. 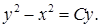 19.6.6.
19.6.6.