
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналогия между вращательным и поступательным движениями
«Я ценю умение строить аналогии, которые, если они смелы и разумны, Используя метод аналогий, можно предположить, что должна существовать замкнутая механическая система, Метод аналогий. Метод исследования какого-либо процесса, путём замены его процессом, Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате s соответствует угол φ, линейной скорости v - угловая скорость w, линейному (касательному) ускорению а - угловое ускорение ε. Сравнительные параметры движения: Поступательное движение |
Вращательное движение | |||||
| Перемещение | S | Угловое перемещение | φ | ||||
| Линейная скорость | 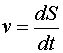
| Угловая скорость | 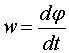
| ||||
| Ускорение | 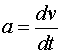
| Угловое ускорение | 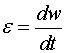
| ||||
| Масса | m | Момент инерции | I | ||||
| Импульс | 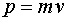
| Момент импульса | 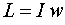
| ||||
| Сила | F | Момент силы | M | ||||
Таблицу можно продолжать и далее.
Работа:
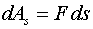
| 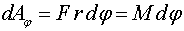
|
Кинетическая энергия
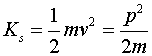
| 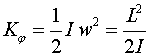
|
Выражения для вращательного движения напоминают соответствующие выражения поступательного движения.
Они получаются из последних формальной заменой m => I, v => w, p => L
Выражения имеют не просто формальное сходство.
Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.
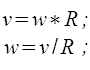
Представленная таблица не может претендовать на всю полноту охвата аналогичных значений.
Для вращательного и поступательного движений формулируются и аналогичные законы:
Закон сохранения импульса (ЗСИ)
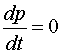 ,при Fвнеш = 0 ,при Fвнеш = 0
| Закон сохранения момента импульса (ЗСМИ)
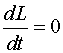 , при Mвнеш = 0 , при Mвнеш = 0
|
Эти законы формулируются следующим образом:
| «Если геометрическая сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, т.е. не меняется со временем. В частности, это имеет место, когда система замкнута» | «Если момент внешних сил относительно неподвижного начала О равен нулю, то момент импульса системы относительно того же начала остается постоянным во времени» | |
| [Д.В.Сивухин. Общий Курс Физики. т.I Механика]
| ||
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях, когда Ньютоновская механика неприменима (релятивистская физика, квантовая механика). Он может быть получен как следствие интуитивно-верного утверждения о том, что свойства нашего мира не изменятся, если все его объекты (или начало отсчета!) переместить на некоторый вектор r. В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.
Закон сохранения момента импульса является следствием утверждения о том, что свойства окружающего мира не изменяются при поворотах (или повороте системы отсчета) в пространстве. Момент импульса системы точечных тел L определяется как сумма моментов каждой из точек и сохраняется во времени при условии равенства нулю момента внешних сил. Данные законы относятся к глобальным законам сохранения.
Ответ на естественный вопрос о том, почему справедливы законы сохранения, в физике был найден сравнительно недавно. Оказалось, что законы сохранения возникают в системах при наличии у них определенных элементов симметрии. (Элементом симметрии системы называется любое преобразование, переводящие систему в себя, т.е. не изменяющее ее).
Немецкий математик Эмми Нётер в 1918 году математически доказала связь между законами сохранения и симметрией, которой обладают в физике законы природы. В упрощенной формулировке теорема Нётер гласит, что если свойства системы не меняются от какого-либо преобразования переменных, то этому соответствует некоторый закон сохранения.
Теорема Нётер - самое простое и универсальное средство, позволяющее находить законы сохранения в классической механике, квантовой механике, теории поля и т.д.
Вот как выглядят доказательства ЗСИ и ЗСМИ на основании свойства симметрии пространства
[Д.В.Сивухин. Общий Курс Физики. т.I Механика.(гл.Y,§38)]:
|
|
.........
… 4.Перейдем к доказательству закона сохранения импульса. Допустим, что механическая система замкнута. Все силы F1, F2,..., действующие на материальные точки системы, являются силами внутренними, внешних сил нет. Перенесем систему из произвольного положения 1 в другое произвольное положение 2, чтобы все материальные точки ее претерпели одно и то же смещение r, и притом так, чтобы их скорости остались прежними по величине и направлению. Ввиду однородности пространства, на такое перемещение не требуется затраты работы. Но эта работа представляется скалярным произведением (F1 +F2 +...) r. Значит, оно равно нулю, каково бы ни было смещение r. Отсюда следует, что для замкнутой системы F1 +F2 +...=0. А это есть как раз то условие, при выполнении которого из второго закона Ньютона получается закон сохранения импульса.
5. Закон сохранения момента импульса для замкнутой системы доказывается в точности так же. Используя изотропию пространства, можно доказать, что геометрическая сумма моментов внутренних сил, действующих в системе, равна нулю: М1 +М2 +...=0. Отсюда немедленно следует рассматриваемый закон
..........
Как видно, доказательства очень похожи.
При всей схожести поступательного и вращательного движений, у них есть и различия.
Одно из них и рассматривается в данной статье.
Существует явление, вступающее, казалось бы, в противоречие с ЗСМИ.
| Замкнутую механическую систему можно повернуть на любой угол с помощью одних только внутренних сил. |
И не только повернуть, но и заставить вращаться.
Как можно повернуть механическую систему с помощью одних только внутренних сил?
Рассмотрим пример.
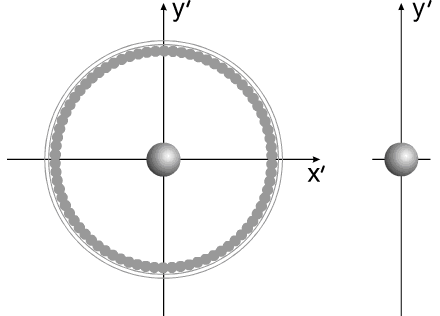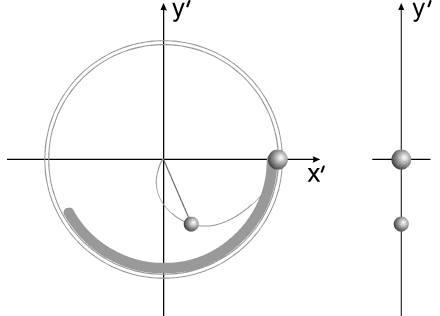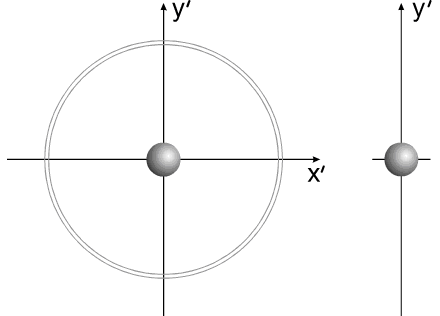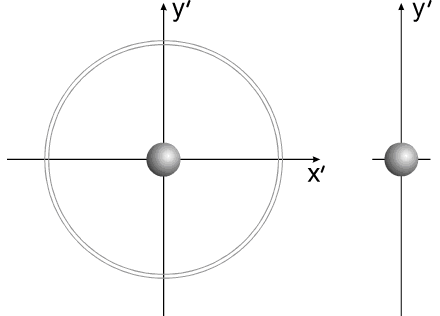
Допустим, у нас имеется два уравновешенных тела, закрепленных соосно. Тела имеют возможность вращаться относительно друг друга. Одно из тел (зеленый контур, красный радиус) способно изменять свои геометрические размеры, изменяя, тем самым, свой момент инерции (Iv). Допустим, максимальное значение Iv max этого тела соответствует значению Ic второго тела (синий контур, пурпурный радиус). Минимальное значение Iv min значительно меньше Iv max.
Рассмотрим циклы движения данной механической системы.
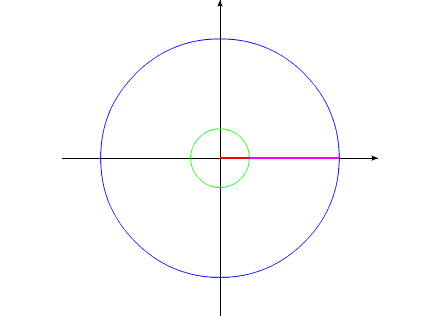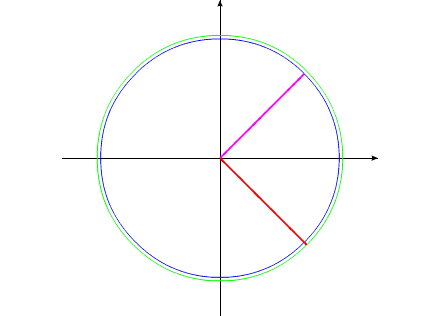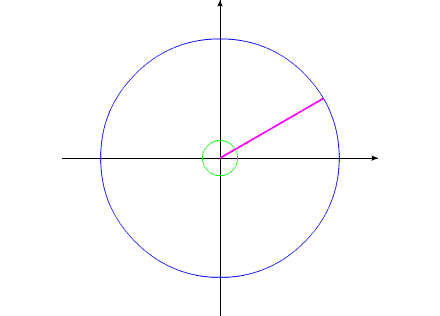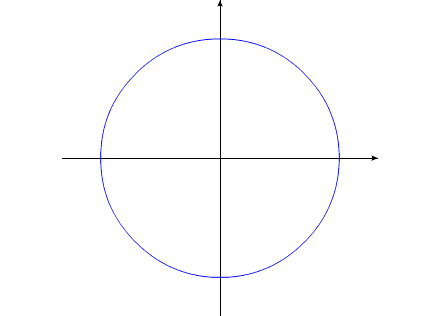
Рис.1
Тело с переменным Iv приобретает максимальные геометрические размеры. (За счет внутренней энергии, разумеется).
За счет той же внутренней энергии создадим внутренний момент, действующий одинаково на оба тела. Под действием этого момента, тела начинают поворачиваться в противоположные направления.
Можно остановить движение обоих тел в любой момент времени. Поскольку моменты инерции обоих тел равны, то и угловые положения оба тела займут одинаковые (по абсолютной величине). В момент останова, угловое положение всей системы осталось прежним. Не изменится это угловое положение и тогда, когда мы начнем изменять геометрические размеры одного из тел.
Уменьшив геометрический размер, и соответственно момент инерции одного из тел, попробуем свести оба тела к прежним угловым положениям этих тел, с помощью силового момента, направленного в другую сторону.
Вот тут и происходит интересное.
|
|
Поскольку моменты инерции обоих тел уже различны, то оба тела повернутся на разные углы. Можно опять увеличить размеры одного из тел. Система вновь будет такой, как и прежде.
Почти…
На самом деле, вся система оказывается повернутой на некоторый угол.
Величина этого угла пропорциональна разнице моментов инерции двух тел.
Эти циклы движения можно повторять.
И оказывается, что система вращается!
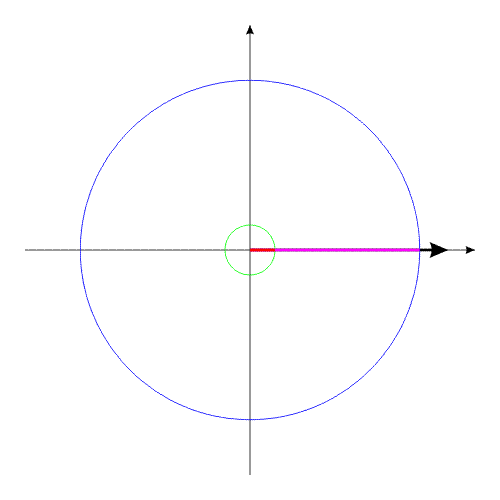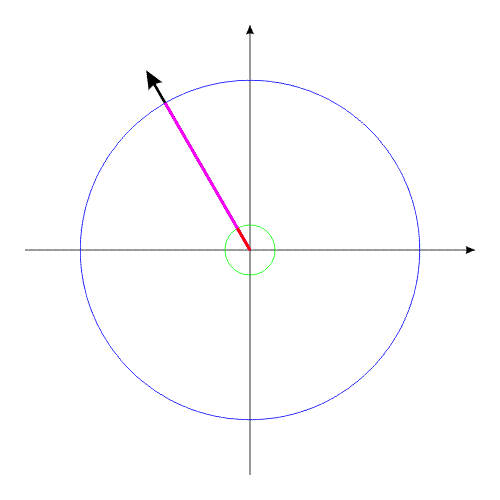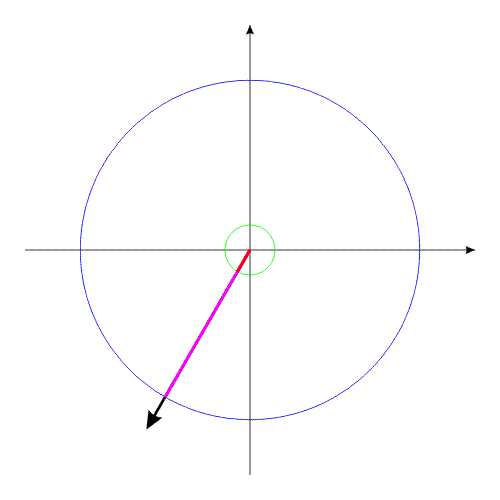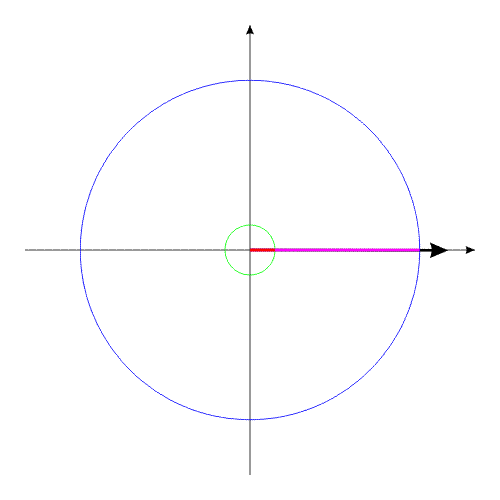
Рис.2
Причем, вращается совсем неплохо!
Допустим, компоненты системы изменяют свои геометрические размеры таким образом, что суммарный момент инерции всей системы остается без изменений.
Изображенную на рис.3 систему можно рассматривать, как взаимодействие тел с переменным моментом инерции, при неизменной массе и неизменном моменте инерции всей системы в целом.
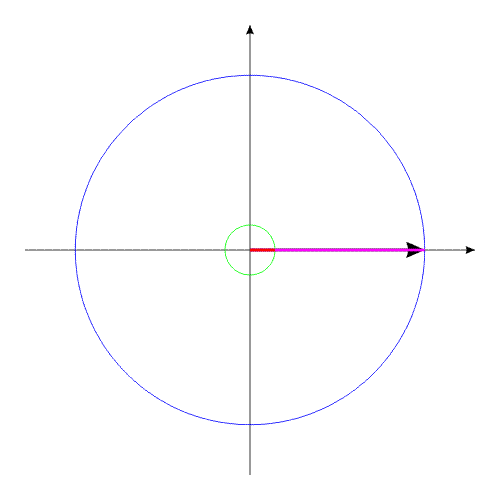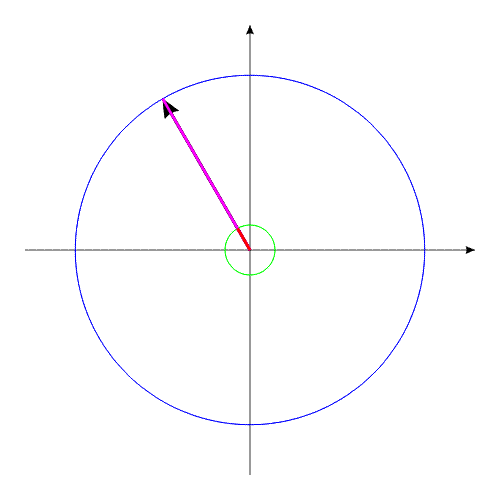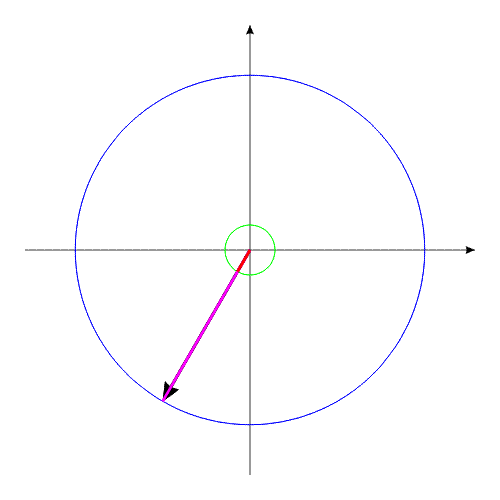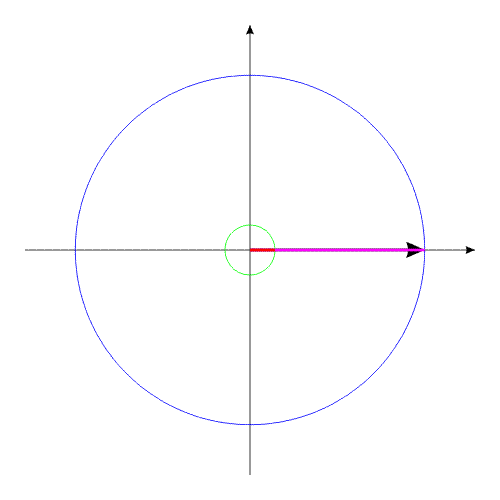
Рис.3
Система, изображенная в анимационном рис.3, совершает полный оборот за 16 секунд.
Можно даже вычислить скорость вращения этой системы:
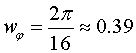 [ рад/с ]
[ рад/с ]
Но, на самом деле, нельзя говорить об этой величине, как о «скорости вращения системы». Правильнее будет звучать: «скорость процесса изменения углового положения», так как величина wφ не является мерой кинетического состояния данной системы, поскольку кинетическая энергия системы не изменяется.
Рассмотренное движение является безынерционным (движением без инерции!). Если остановить относительные перемещения компонентов внутри замкнутой системы, движение wφ немедленно прекращается. К величине wφ более всего подходит название скорость прецессии.
В процессе подобного вращения не нарушается ЗСМИ, поскольку суммарный момент импульса всех компонентов системы, в каждый момент времени, равен нулю. В то же время можно определить момент силы, эквивалентный внешнему моменту силы, который необходимо было бы приложить к системе, чтобы вызвать подобное перемещение. Именно – эквивалентный, поскольку для рассматриваемой ситуации, внешний силовой момент равен нулю.
Примечание. безынерционный - безынерционный [безынерционный] прил. Практически не обладающий инерцией, мгновенно реагирующий на внешнее воздействие.
Так определяется значение этого слова в Толковом словаре русского языка под редакцией Т. Ф. Ефремовой.
Мне бы хотелось добавить, что гораздо более важным свойством, определяющим "безинерционность", является факт отсутствия движения при снятии воздействия (применительно к механическим системам).
|
|
Поиск в русскоязычной части Википедии по слову "безынерционность" говорит о том, что такой страницы не существует.
В статье Википедии "Прецессия" есть упоминание о безынерционных свойствах прецессии:
" Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве ".
Еще совсем недавно (сентябрь 2009) ссылка со слова " безынерционность " с этой страницы, отсылала "в никуда". Вики предлагала создать такую страничку.
Но сейчас, у этого слова в данной статье, появилась гиперссылка на статью "Инерция".
Кто, зачем, с какой целью так поступил - не очень понятно. Возможно, тем самым просто закрыли пустую ссылку.
Или просто связали слово " безынерционность " со словом " инерция ", чтобы не возникало каких-либо разночтений.
Поэтому, совершенно случайно, возник вопрос:
Нужна ли статья "Безынерционность" в Википедии?
Этот вопрос я хотел бы задать именно Вам и именно здесь.
Выводы, которые можно сделать на основании приведенного примера:
- в рамках Закона Сохранения Момента Импульса можно изменять угловые координаты замкнутой механической системы только за счет внутренних сил;
- важную роль при организации углового перемещения с помощью внутренних сил, играет изменение момента инерции компонентов системы;
- угловое перемещение всей системы - безынерционно;
- скорость изменения угловых координат, имея размерность такую же, как и угловая скорость, скоростью может считаться только формально.
Вернемся к доказательствам ЗСИ и ЗСМИ на основании свойства симметрии пространства.
Доказательства строятся на допущении некоторого смещения системы (поворота, в случае ЗСМИ).
Но в случае вращающейся системы, это смещение действительно можно произвести за счет внутренней энергии.
То есть, смещение не виртуально, а вполне реально.
В большой таблице аналогичных выражений для вращательного и поступательного перемещений, появляется большая пустая ячейка:
| Перемещение за счет внутренних сил ? | Поворот за счет внутренних сил
φ ≠ const при: ∑ L i= 0, 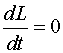 , Mвнеш = 0 , Mвнеш = 0
|
Перемещение за счет внутренних сил?
В случае с поступательным перемещением, такое, кажется, недопустимо. На этот счет даже существует «Теорема о движении центра масс», которая, на первый взгляд, не допускает подобное перемещение:
«Центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила — геометрической сумме всех внешних сил, действующих на систему».
Значит, пустую ячейку в таблице должна занимать данная теорема?
Но метод аналогий позволяет предположить, что и для линейно перемещающейся системы, должны существовать возможности, присущие вращающейся системе.
Это предположение строится на аналогичности уравнений движения вращательного и поступательного движений.
Ячейка должна быть заполнена, примерно, следующим содержанием:
|
|
Перемещение за счет внутренних сил
s ≠ const при: ∑ p i= 0, 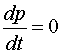 , Fвнеш = 0 , Fвнеш = 0
|
Это выражение получается в результате формальной замены φ => S, M => F, L => p
Выводы, которые можно сделать с помощью метода аналогий:
- возможно существование механической системы, которая способна линейно перемещаться только за счет внутренних сил;
- линейное перемещение может осуществляться за счет изменения параметра, аналогичного моменту инерции, а именно – массы;
- линейное перемещение всей системы должно быть безынерционным;
· «скорость» перемещения подобной системы не будет являться мерой кинетического состояния, т.е. в процессе перемещения суммарный импульс компонентов системы будет оставаться неизменным.
Поскольку «скорость» при таком движении является величиной формальной, её появление не может служить признаком нарушения «Теоремы о движении центра масс».
Варипенд (Varipend)
Свойства механической системы, под названием " варипенд ", полностью удовлетворяют перечисленным предположениям.
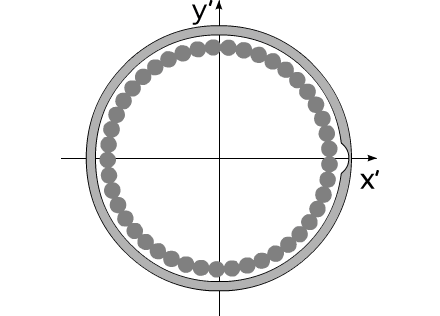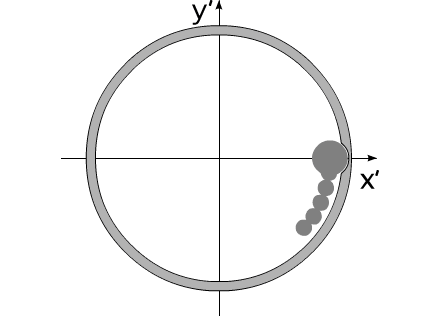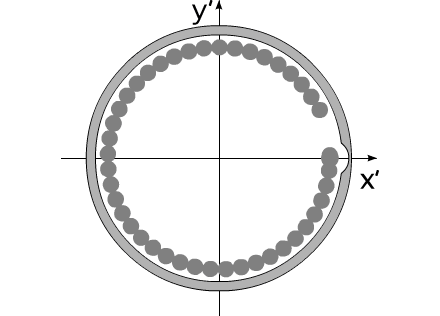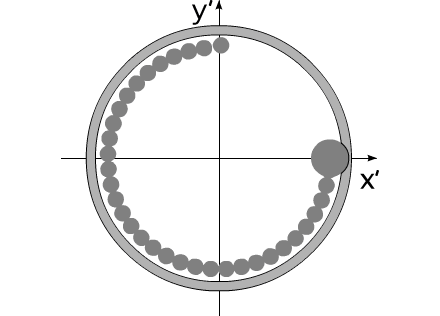
Рис.4
Название " варипенд " получено от слияния двух слов: varipend = vari able + pend ulum (переменный маятник).
В процессе перемещения рабочей массы и её остановке в "корпусе" системы, движение центра масс рабочего вещества можно рассматривать, как движение маятника переменной длины и переменной массы. (В системе координат, связанной с корпусом)

Рис.5
Или, в проекции на одну координату:
(Такой случай перемещения центра масс возможен при перемещении двух рабочих масс, вращающихся в противоположных направлениях.)
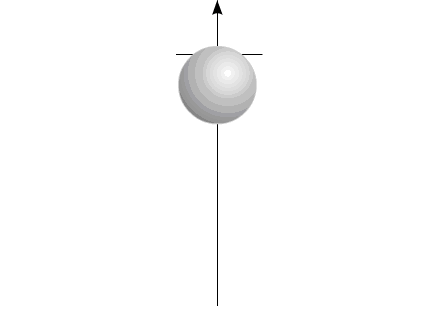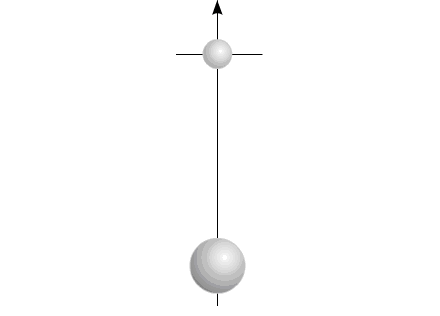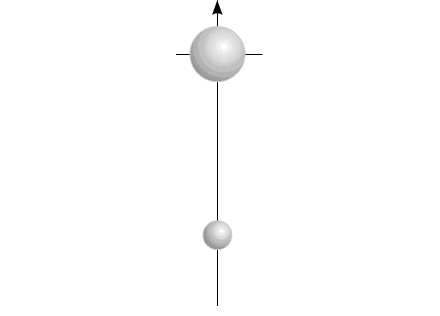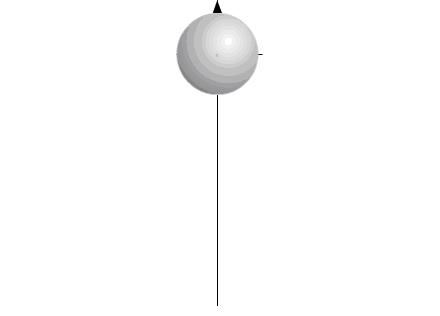
Рис.6
Изменяющийся размер компонентов на рисунке символизирует изменение массы элементов системы:
рабочего вещества, уменьшающего свою массу за рабочий период,
и корпуса системы, увеличивающего свою массу за счет присоединения частиц рабочего вещества.
| При неизменной общей массе, всю систему можно рассматривать, как взаимодействие компонентовпеременной массы. |
Единственной причиной изменения импульса корпуса является приобретение корпусом элементарных импульсов рабочей массы. При этом корпус увеличивает свою массу.
Единственная причина изменения импульса рабочей массы – потеря элементарных импульсов частиц рабочей массы. При этом масса рабочего вещества уменьшается.
При этом изменение импульса всей системы равно нулю.
И суммарный импульс всей системы также равен нулю!
В одном из расчетов перемещения "варипенда" используется уравнение движения тела переменной массы – уравнение Мещерского.
Расчет перемещения данной механической системы с помощью уравнений Лагранжа также приводит к интересному результату...
На рис.4 представлена постановка задачи "варипенд".
Решение этой задачи выглядит следующим образом:
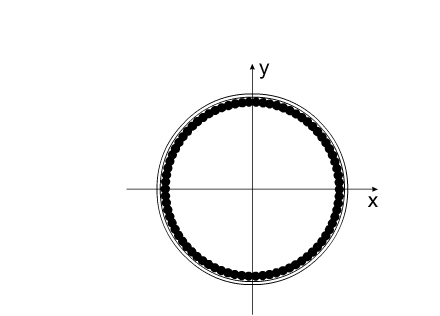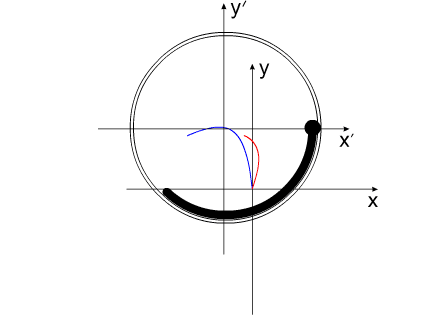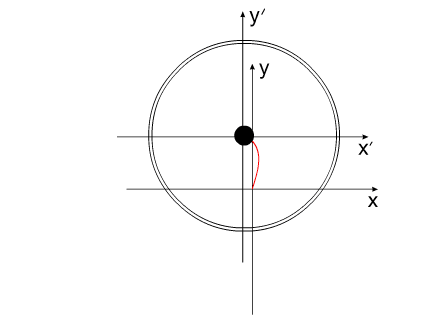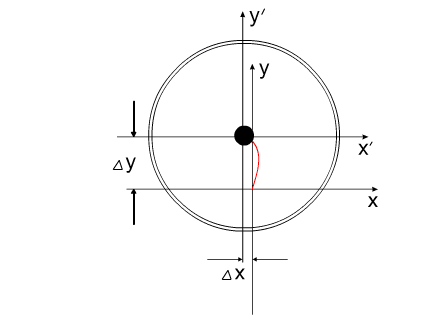
Синим цветом показана траектория перемещения корпуса.
Красным - перемещение Центра Масс всей системы.
рис.7
При перемещении "варипенда" не совершается работа.
Если рассматривать "варипенд" в абсолютной системе координат, то при повторении внутренних циклов перемещения рабочего вещества, "варипенд" непрерывно изменяет свое положение в пространстве:
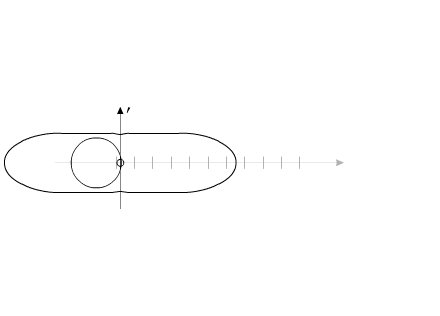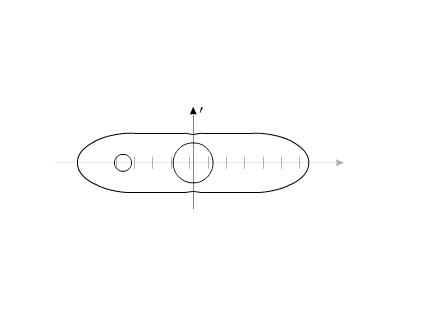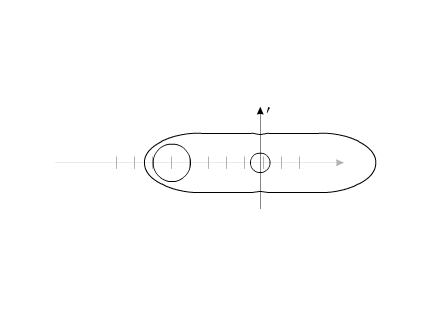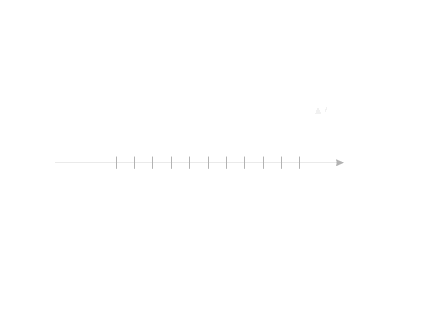
Рис.8
Можно провести аналогию с рисунком 3.
Система, изображенная на рис.8, перемещается на расстояние 55 мм за 20 секунд.
Казалось бы, можно подсчитать скорость "варипенда":
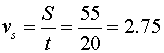 [мм/с]
[мм/с]
Но так как в процессе перемещения суммарный импульс системы остается неизменным, величина vs будет являться величиной формальной, определяющей только изменения координат центра масс. Эта величина никак не связана с импульсом всей системы.
Перемещение "варипенда" является безынерционным.
Если остановить относительное перемещение рабочей массы внутри замкнутой механической системы, вся система мгновенно прекратит свое движение.
Математические расчеты, описывающие свойства механической системы под названием «варипенд», можно посмотреть по адресу:
https://varipend.narod.ru
Примечание
Во многих учебных изданиях по Теоретической Механике, приводятся примеры поворота замкнутой механической системы за счет внутренних сил.
Например, человек способен повернуть себя на скамье Жуковского, совершая некоторые вращения руками.
Поворачивая массивные тела в космическом летательном аппарате, производят угловую ориентацию этих аппаратов.
Космонавт, находясь в невесомости, также может повернуть свой корпус, совершив несколько оборотов рукой.
Однако, на самом деле, во всех приведенных примерах поворот системы отсутствует.
Приведенные примеры демонстрируют, если можно так выразиться, "теорему о сохранении углового положения" замкнутой механической системы.
Попытаюсь пояснить свои слова.
Если моменты инерции компонентов системы не изменяются и внешний момент отсутствует, то можно записать:
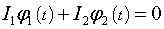
Это легко проверить.
Допустим, мы поворачиваем два тела друг относительно друга.
Если после остановки поворачивать компоненты в противоположную сторону, система обязательно займет точно такое же угловое положение, которое было в начальный момент времени.
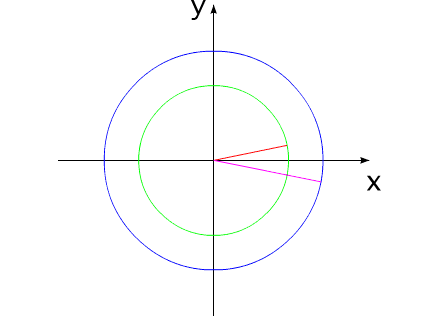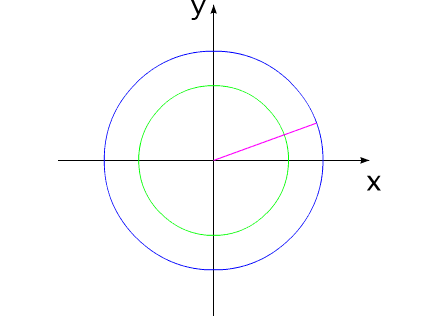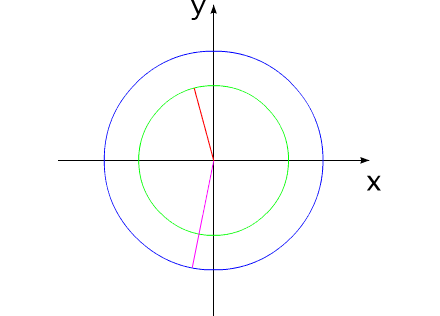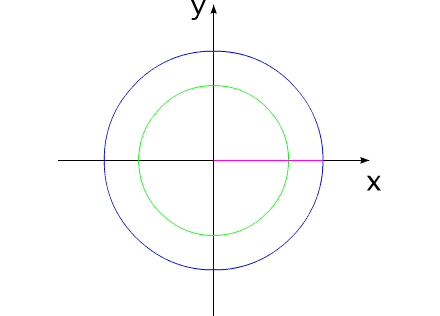
Рис.9
На рис.9 два тела сначала поворачиваются на некоторый угол, а затем поворачиваются в противоположную сторону на точно такие же углы. При этом система занимает свое прежнее угловое положение.
Иллюзия поворота всей системы возникает из-за того, что угловая функция периодична. Как только угловые положения компонентов превышают угол 2π, возникает ощущение, что система повернулась. Но это не так. Конечно же, углы необходимо продолжать отсчитывать и при превышении угла 2π.
Аналогичным примером линейного перемещения может служить случай взаимодействия двух тел, обладающих неизменной массой:
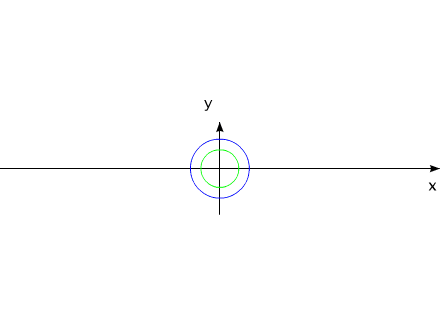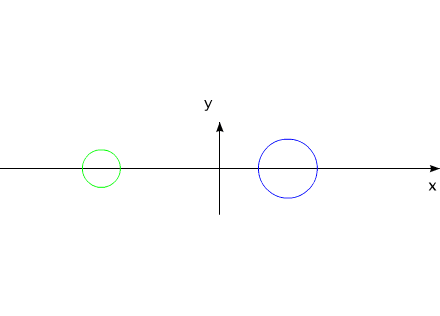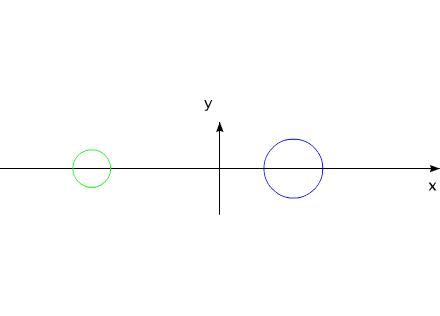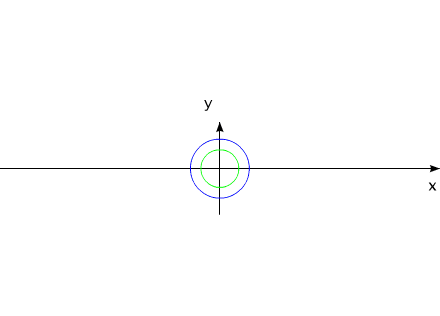
Рис.10
Тела могут удалятся друг от друга, за счет внутренних сил, приближаться, но для данной системы всегда будет выполняться соотношение:
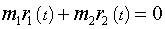
Это - следствие теоремы о движении центра масс....
А как будут выглядеть те же выражения для условий системы, состоящей из компонентов с переменным моментом инерции (переменной массой)?:

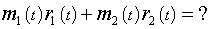 комментарий к "знакам вопроса"...
комментарий к "знакам вопроса"...
|
// 

комментарий к статье "Аналогия между вращательным и поступательным движениями"
В физике, в разделе "Механика", никогда не существовало закона (теоремы, постулата, аксиомы и т.д.), который бы строго-настрого запрещалперемещаться замкнутой механической системе только с помощью внутренних взаимодействий. Такой, с позволения сказать, «закон» невозможно сформулировать и доказать. Попытка сформулировать этот «закон» сразу же войдет в противоречие с Первым законом Ньютона:
«материальная точка (или Центр Масс замкнутой механической системы) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет ее из этого состояния».
А доказать «неподвижность замкнутой механической системы без внешнего воздействия» невозможно вот по какой причине:
В общем случае, для сложной механической системы (т.е., для системы с числом взаимодействующих тел 3 и более), поведение ЦМ – неопределённо.
Для механической системы из трех и более тел, уравнение движения центра масс такой системы может иметь такой вид:
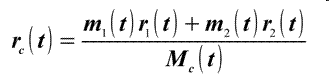 , при , при  где:
где: 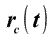 - радиус вектор ЦМ - радиус вектор ЦМ
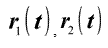 - радиус векторы ЦМ компонентов - радиус векторы ЦМ компонентов
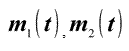 - массы компонентов - массы компонентов
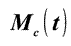 - суммарная масса взаимодействующих компонентов.
Для механической системы из трех и более тел уравнение движения центра масс не имеет общего решения! (В том числе, при нулевых начальных условиях.) - суммарная масса взаимодействующих компонентов.
Для механической системы из трех и более тел уравнение движения центра масс не имеет общего решения! (В том числе, при нулевых начальных условиях.)
 Что скрывается за знаком вопроса в общем уравнении движения центра масс?
Решению этого уравнения удовлетворяет бесконечное множество траекторий ЦМ,лежащих в некоторой области внутри замкнутой механической системы. При сохранении суммарного импульса системы.
Траекторий! Точка с координатами «0,0,0» - только один частный случай из бесконечного множества траекторий!
Это дифференциальное уравнение может решаться только для частных случаев, то есть, накладывая те или иные ограничения на свойства и условия взаимодействий компонентов системы (т.е. зная функции
Что скрывается за знаком вопроса в общем уравнении движения центра масс?
Решению этого уравнения удовлетворяет бесконечное множество траекторий ЦМ,лежащих в некоторой области внутри замкнутой механической системы. При сохранении суммарного импульса системы.
Траекторий! Точка с координатами «0,0,0» - только один частный случай из бесконечного множества траекторий!
Это дифференциальное уравнение может решаться только для частных случаев, то есть, накладывая те или иные ограничения на свойства и условия взаимодействий компонентов системы (т.е. зная функции  и опираясь на законы сохранений).
Одним из таких частных случаев является случай взаимодействия двух тел (или сводя все взаимодействия замкнутой механической системы к взаимодействию двух тел). и опираясь на законы сохранений).
Одним из таких частных случаев является случай взаимодействия двух тел (или сводя все взаимодействия замкнутой механической системы к взаимодействию двух тел).
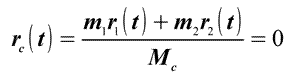 «Равно нулю» – при нулевых начальных условиях.
Но распространять одно частное решение на все случаи взаимодействий в любых изолированных механических системах - является грубой ошибкой. От «частного» нельзя перейти к «общему».
1. ЦМ – это просто геометрическая координата. Результат математической функции. 2. Эта координата зависит: как от координат всех компонентов системы, так и от масс этих компонентов. 3. Изменяться с течением времени могут: как координаты компонентов системы, так и массы компонентов системы 4. ЦМ не обладает массой (см.п.1) 5. ЦМ не обладает импульсом (см.п.4) 6. Не обладает инерцией (см.п.4) 7. Функция координат ЦМ непрерывна и неразрывна Rc (t)=f(ri (t),mi (t)) 8. Масса изолированной системы неизменна. Константа. Но эта константа есть функция от времени: Mc (t)=m1 (t)+m2 (t)=const. Функция координат ЦМ может иметь такой вид: Rc (t)=const(t) Так описывается безынерционное перемещение. Выражение:
«Равно нулю» – при нулевых начальных условиях.
Но распространять одно частное решение на все случаи взаимодействий в любых изолированных механических системах - является грубой ошибкой. От «частного» нельзя перейти к «общему».
1. ЦМ – это просто геометрическая координата. Результат математической функции. 2. Эта координата зависит: как от координат всех компонентов системы, так и от масс этих компонентов. 3. Изменяться с течением времени могут: как координаты компонентов системы, так и массы компонентов системы 4. ЦМ не обладает массой (см.п.1) 5. ЦМ не обладает импульсом (см.п.4) 6. Не обладает инерцией (см.п.4) 7. Функция координат ЦМ непрерывна и неразрывна Rc (t)=f(ri (t),mi (t)) 8. Масса изолированной системы неизменна. Константа. Но эта константа есть функция от времени: Mc (t)=m1 (t)+m2 (t)=const. Функция координат ЦМ может иметь такой вид: Rc (t)=const(t) Так описывается безынерционное перемещение. Выражение:
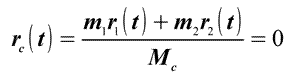 (1)
определяет радиус-вектор ЦМ механической системы, состоящей из 2 (двух) тел. Или радиус-вектор Центра Масс системы из любого произвольного числа взаимодействующих тел, но сводя все взаимодействия к взаимодействию 2 (двух тел). (Рис.1) (1)
определяет радиус-вектор ЦМ механической системы, состоящей из 2 (двух) тел. Или радиус-вектор Центра Масс системы из любого произвольного числа взаимодействующих тел, но сводя все взаимодействия к взаимодействию 2 (двух тел). (Рис.1)
 рис.1
Все взаимодействия внутри изолированной механической системы сводятся к взаимодействию двух тел согласно парности всех сил в соответствии с Третьим законом Ньютона: " Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению ": рис.1
Все взаимодействия внутри изолированной механической системы сводятся к взаимодействию двух тел согласно парности всех сил в соответствии с Третьим законом Ньютона: " Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению ":
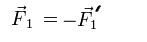 Выражение (1) определяет координаты точки C0 , в которую может быть собрана (стянута) вся механическая системы с помощью всех парных взаимодействий внутри этой механической системы.
Равенство "Нулю" радиус-вектора ЦМ возможно при "нулевых" начальных условиях, т.е. при начальной скорости, ускорении и начальных координатах ЦМ, равных нулю.
В то же время, выражение для радиус-вектора ЦМ сложной механической системы:
Выражение (1) определяет координаты точки C0 , в которую может быть собрана (стянута) вся механическая системы с помощью всех парных взаимодействий внутри этой механической системы.
Равенство "Нулю" радиус-вектора ЦМ возможно при "нулевых" начальных условиях, т.е. при начальной скорости, ускорении и начальных координатах ЦМ, равных нулю.
В то же время, выражение для радиус-вектора ЦМ сложной механической системы:
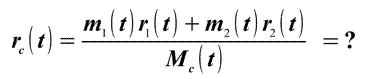 (2)
говорит о том, что координаты ЦМ, с течением времени, могут быть "любыми"(Рис.2). (2)
говорит о том, что координаты ЦМ, с течением времени, могут быть "любыми"(Рис.2).
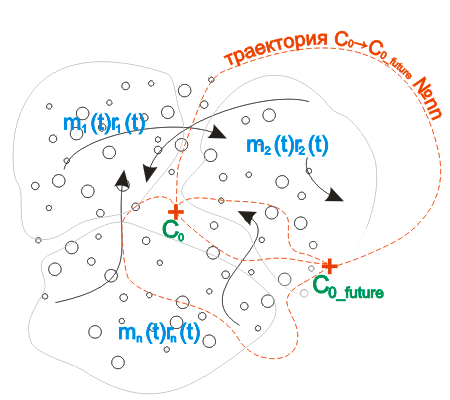 рис.2
C помощью выражения (1): рис.2
C помощью выражения (1): 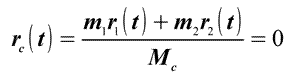 мы можем определить координаты ЦМ (точки C0) в настоящий момент времени.
Но мы не можем, не имеем права, утверждать, что ЦМ сложной механической системы всегда, в любой момент времени, будет находиться в точке C0. В сложной механической системе могут существовать взаимодействия вида: ri (t),mi (t) (см.рис.2) и в некоторый момент времени координаты ЦМ могутоказаться в точке C0_ future
При этом, траектория перемещения к точке C0_ future может быть любая (условие: неразрывная и непрерывная). И таких траекторий может быть неограниченное количество. В полном соответствии с законами сохранения: законом сохранения суммарного импульса и с законами сохранений массы и энергии изолированной механической системы.
Но в любой момент времени, к любой механической системе может быть применен метод (1), определяющий частное решение координат ЦМ: мы можем определить координаты ЦМ (точки C0) в настоящий момент времени.
Но мы не можем, не имеем права, утверждать, что ЦМ сложной механической системы всегда, в любой момент времени, будет находиться в точке C0. В сложной механической системе могут существовать взаимодействия вида: ri (t),mi (t) (см.рис.2) и в некоторый момент времени координаты ЦМ могутоказаться в точке C0_ future
При этом, траектория перемещения к точке C0_ future может быть любая (условие: неразрывная и непрерывная). И таких траекторий может быть неограниченное количество. В полном соответствии с законами сохранения: законом сохранения суммарного импульса и с законами сохранений массы и энергии изолированной механической системы.
Но в любой момент времени, к любой механической системе может быть применен метод (1), определяющий частное решение координат ЦМ:
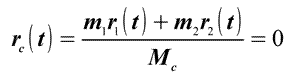 Т.е., применяя третий закон Ньютона, используя парные взаимодействия, мы можем стянуть всю систему в точку C0 В каждый момент времени (при стягивании всей системы в точку C0) - система неподвижна. Скорость ЦМ равна нулю. Но если действительно стянуть всю систему в точку C0, то исчезнет, так и не появившись, будущая, возможная, вероятная точка C0_ future...
Т.е., применяя третий закон Ньютона, используя парные взаимодействия, мы можем стянуть всю систему в точку C0 В каждый момент времени (при стягивании всей системы в точку C0) - система неподвижна. Скорость ЦМ равна нулю. Но если действительно стянуть всю систему в точку C0, то исчезнет, так и не появившись, будущая, возможная, вероятная точка C0_ future...
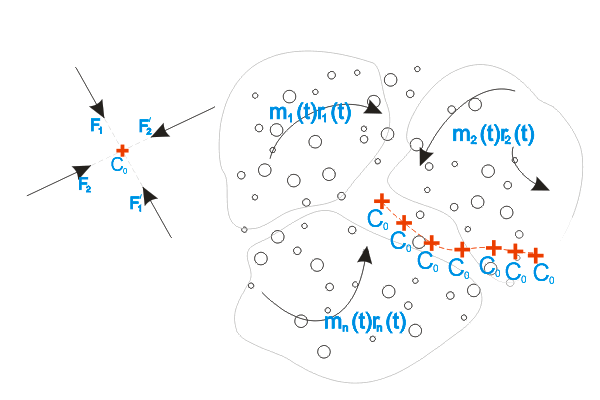 рис.3
Собственно, именно такой "набор точек C 0 " и представляет собой траекториюбезынерционного перемещения механической системы Varipend (Варипенд).
Набор точек " возможного стягивания в точкуC 0 "... Набор частных решений рис.3
Собственно, именно такой "набор точек C 0 " и представляет собой траекториюбезынерционного перемещения механической системы Varipend (Варипенд).
Набор точек " возможного стягивания в точкуC 0 "... Набор частных решений 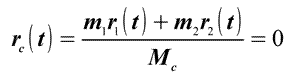 общего уравнения ЦМ: общего уравнения ЦМ: 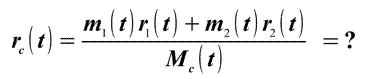 .... ....
|
С.В.Бутов
7 июля 2007
" ... аналогия является специфическим случаем симметрии, особым видом единства сохранения и изменения. Следовательно, использовать в анализе метод аналогии, — значит действовать в соответствии с принципом симметрии. Аналогия не только допустима, но и необходима в познании природы вещей.... " [Овчинников Н. Ф. Принципы сохранения,.М.,1966]
Новиков Н.Б. "1000 аналогий, изменивших науку".
| Дополнительные ссылки: · статья "Нереактивное перемещение" |
Нереактивное перемещение.
С.В.Бутов
Автор статьи не придумывает новые физические законы, и ни в коем случае не пытается нарушить действующие.
Для замкнутой системы, то есть системы, не испытывающей внешних воздействий, или в случае, когда геометрическая сумма действующих на систему внешних сил равна нулю, имеет место закон сохранения количества движения. При этом количество движения отдельных частей системы (например, под действием внутренних сил) могут изменяться, но так, что величина 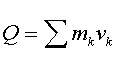 остаётся постоянной.
остаётся постоянной.
Этот закон объясняет такие явления, как реактивное движение, отдачу (или откат) при выстреле, работу гребного винта или вёсел и др.
Например, если рассматривать ружье и пулю как одну систему, то давление пороховых газов при выстреле будет для этой системы силой внутренней и не может изменить количество движения системы, равное до выстрела нулю. Поэтому, сообщая пуле количество движения 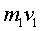 , направленное к дульному срезу, пороховые газы сообщат одновременно ружью численно такое же, но противоположно направленное количество движения
, направленное к дульному срезу, пороховые газы сообщат одновременно ружью численно такое же, но противоположно направленное количество движения  , что вызовет отдачу. Из равенства
, что вызовет отдачу. Из равенства 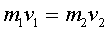 (где
(где 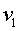 ,
, 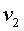 — численные значения скоростей) можно, зная скорость
— численные значения скоростей) можно, зная скорость 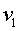 пули при вылете из ствола, найти наибольшую скорость
пули при вылете из ствола, найти наибольшую скорость 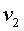 отдачи (а для орудия — отката).
отдачи (а для орудия — отката).
В приведенном примере тела приобретают скорости под действием импульса силы 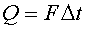 , величина которого равна для обоих тел, но противоположна по направлению (Рис.1).
, величина которого равна для обоих тел, но противоположна по направлению (Рис.1).
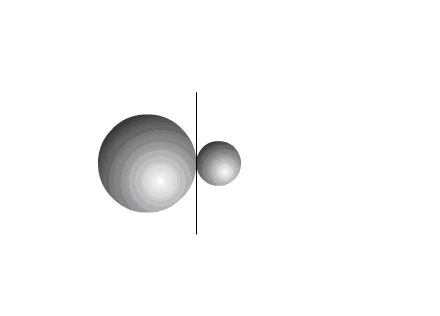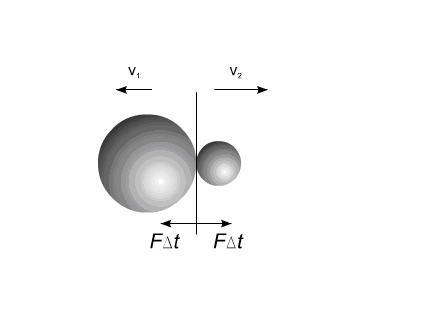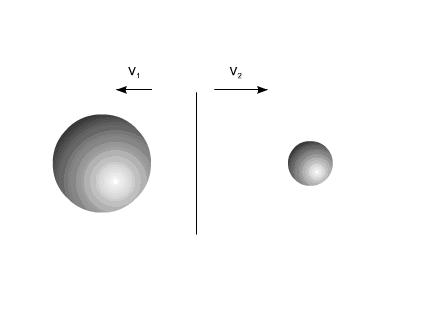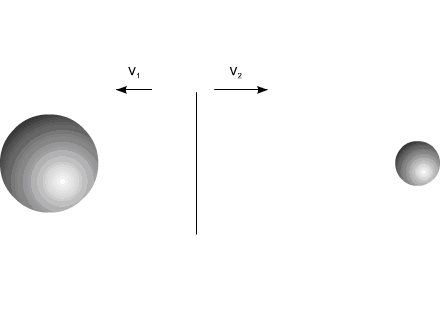
Рис. 1
После воздействия импульса силы тела двигаются прямолинейно и равномерно.
Центр масс всей системы, после разлета компонентов, сохраняет свою первоначальную скорость.
Если рассматривать ракету и продукты сгорания ракетного топлива как единую механическую систему, то центр масс этой системы также сохраняет неизменным свое положение. (В системе отсчета, связанной с точкой старта.)
В то же время возможна ситуация, когда компоненты системы тел приобретают количество движения не за счет явно выраженного импульса силы.
Компоненты системы тел могут приобрести количество движения, потому что уже обладают импульсами, имеют какую-то кинетическую энергию.
Рассмотрим следующий пример.
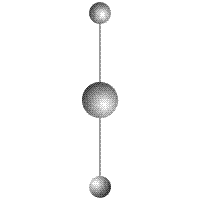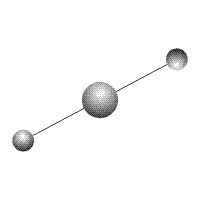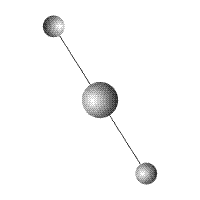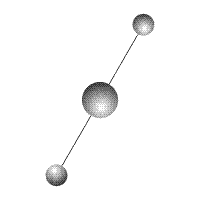
Рис. 2
Вокруг тела массой 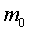 вращаются два тела одинаковой массы
вращаются два тела одинаковой массы 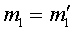 (Рис.2). Все тела соединены жесткими неразрывными связями. Вращение с угловой скоростью
(Рис.2). Все тела соединены жесткими неразрывными связями. Вращение с угловой скоростью 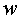 происходит вокруг общего центра масс системы, совпадающего, в данном случае, с центром масс тела
происходит вокруг общего центра масс системы, совпадающего, в данном случае, с центром масс тела 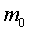 . Система тел уравновешена. Ее центр масс неподвижен. Проекции количества движения на оси координат равны нулю.
. Система тел уравновешена. Ее центр масс неподвижен. Проекции количества движения на оси координат равны нулю.
Если в некоторый момент времени разорвать одну из связей, то компоненты системы начнут перемещаться в противоположных направлениях.
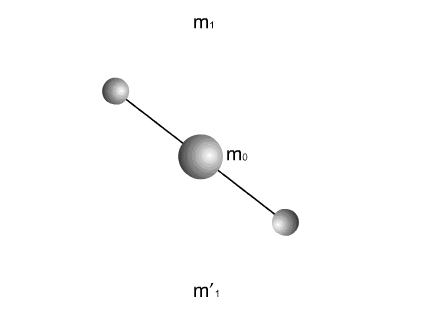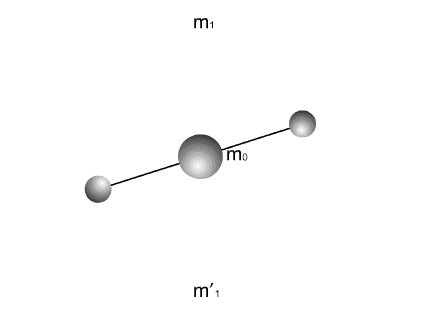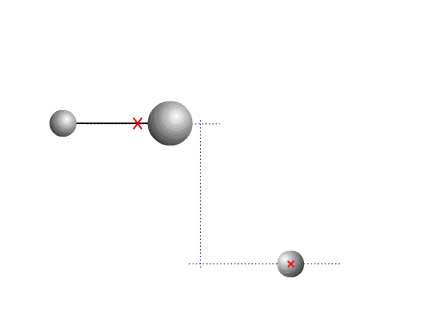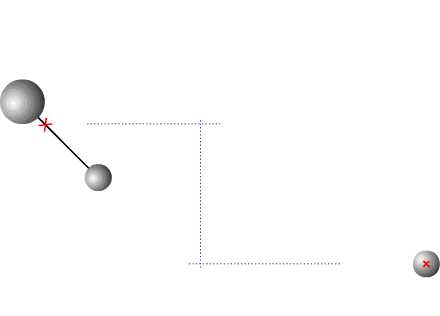
Рис. 3
После обрыва связи система распадается на два компонента: тело  и систему из двух связанных тел
и систему из двух связанных тел 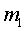 и
и 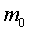 (Рис.3).
(Рис.3).
Тело  будет двигаться прямолинейно и равномерно по касательной к траектории своего движения в момент обрыва связи.
будет двигаться прямолинейно и равномерно по касательной к траектории своего движения в момент обрыва связи.
Система тел 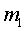 и
и 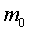 также будет двигаться прямолинейно и равномерно. Количество движения этой системы, по абсолютной величине, будет равно количеству движения
также будет двигаться прямолинейно и равномерно. Количество движения этой системы, по абсолютной величине, будет равно количеству движения 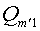 :
:
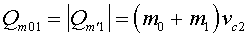
, где 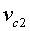 — скорость центра масс системы тел
— скорость центра масс системы тел 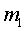 и
и 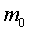 .
.
Следует подчеркнуть, что выражение «прямолинейно и равномерно» относится только к центру масс рассматриваемой системы (отмечен красным цветом на Рис.3). Компоненты системы, в то же время, приобретают неравномерные относительные скорости перемещения относительно общего центра масс.
Если тело 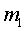 в начальный момент времени, сразу после обрыва связи, двигается так же, как и тело
в начальный момент времени, сразу после обрыва связи, двигается так же, как и тело  (по абсолютному значению), то для тела
(по абсолютному значению), то для тела 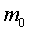 начальная скорость равна нулю.
начальная скорость равна нулю.
Таким образом, тело 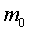 «запаздывает», его скорость заметно отстает от скорости центра масс в начальный момент времени, сразу после обрыва связи. Можно показать чуть помедленнее (рис.4).
«запаздывает», его скорость заметно отстает от скорости центра масс в начальный момент времени, сразу после обрыва связи. Можно показать чуть помедленнее (рис.4).
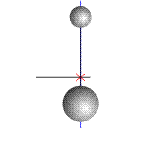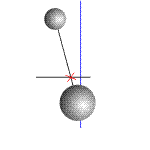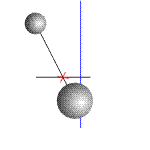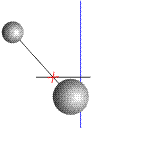
Рис. 4
Этот процесс «запаздывания» можно увеличить, "растянуть во времени".
Допустим, на борту некоего летательного аппарата, покоящегося в невесомости, установлена кольцевая центрифуга, равномерно заполненная по всей окружности дробинками. Центрифуге придается вращательное движение. Ось центрифуги совпадает с центром масс летательного аппарата. В некоторый момент времени, дробинки начинают покидать центрифугу. Покидают последовательно, друг за другом, из одной и той же точки, относительно корпуса летательного аппарата.



