Представление графа в виде списка дуг

 

Иногда используются и другие представления графов, например, для случая очень разреженных графов, когда при большом количестве N вершин графа число дуг существенно меньше NXN, например, порядка N. Одним из таких представлений является представление в виде списка дуг, когда все дуги графа собраны в единый список, в каждом элементе которого записана информация об обоих концах дуги, а также, возможно, о нагрузке на дугу (рис.3).

 

Рис.3. Граф и его представление в виде списка дуг

 

В листинге приведено представление графа в виде списка дуг. Такое представление будем называть A-графом от слова Arc— дуга. Список дуг представлен списком элементов, каждый из которых содержит два целых числа— номера концов дуги. В данной реализации список не представлен в виде отдельного описания класса. Вместо этого описание элемента такого списка— дуги— внесено прямо в описание класса для представления A-графа, а реализации операций над списком просто являются частью реализации операций над дугами графа.

Операция добавления дуги в этом представлении — это просто операция добавления одного элемента в конец списка, и реализуется она сравнительно эффективно. Напротив, при выполнении операции поиска дуги может потребоваться просмотреть весь список. Разумеется, настолько же неэффективной будет и операция удаления дуги.

 

файл ArcGraph.h

#include "graph.h"                         // Определение родительского класса

// Описание класса для представления A-графа

class ArcGraph: public Graph {

// Дуга представлена элементом списка, содержащим номера

// концов дуги и указатель на следующий элемент списка

struct Arc {

int begin, end;

Arc *next;

 

// Конструктор дуги.

Arc{int b, int e, Arc *n = NULL) {

begin = b; end = e; next = n;)

};

 

// Список дуг представлен, как обычно,

// указателями на первый и последний элементы списка

Arc *first, *last;

 

// arcCount - счетчик числа дуг-элементов списка

 int arcCount;

 

// vertexNumber - количество вершин графа, используемое

//в данном представлении только для контроля номеров вершин

 int vertexNumber;

 

public:

 

// Конструктор графа инициализирует пустой список

 // и запоминает количество вершин графа.

ArcGraph(int n) {

first = last = NULL; arcCount = 0; vertexNumber = n;

}

 

// Функция подсчета количества вершин выдает запомненное значение

 int vertexCoun() const { return vertexNumber; }

 

// Операции над дугами:

void addArc(int from, int to);

bool hasArc(int from, int to) const;

};

 

файл ArcGraph.cpp      

«include "ArcGraph.h"

 

//Реализация операции добавления дуги

void ArcGraph::addArc(int from, int to) {

// Сначала проверяем правильность задания номеров вершин.

if (from < 0 || to < 0 || from >= vertexNumber || to >=vertexNumber)

 return;

Arc *newArc = new Arc(from, to);

// Новая дуга добавляется в конец списка

if (last) last->next = newArc; else first = newArc;

last = newArc;

arcCount++;

}

 

// Реализация операции проверки наличия дуги.

bool ArcGraph::hasArc(int from, int to) const {

 

// Необходимо просмотреть список дуг в поисках нужной.

for (Arc *current = first; current; current = current->next) {

if (current->begin == from && current->end == to)

return true;

}

return false;

}

 

Конечно, выбирать представление графа для решения конкретной задачи нужно исходя из того, какие операции с графами будут выполняться чаще всего. Если в процессе работы граф часто меняет структуру связей, то, наверное, лучшим способом представления будет матрица смежности. Если наиболее частой операцией будет поиск путей в графе, проходящих по направлению дуг, то более удобным и выгодным способом будет способ представления графа в виде списков смежности.

Однако иногда бывает, что выбрать какой-то один способ представления графа трудно, например, потому, что в разные периоды времени работы программы требуется выполнять различные операции. В этом случае было бы удобно переходить от одного представления графа к другому. К счастью, такие преобразования занимают не очень много времени. Конечно, для преобразования придется, по крайней мере, один раз просмотреть весь граф, но время, затраченное на построение нового представления, всегда будет прямо пропорционально размеру графа. Это означает, что если время работы некоторого алгоритма на графе имеет порядок сложности не меньше размера графа, то скорость его работы практически не зависит от способа представления графа, поскольку всегда можно перед началом работы выполнить нужное преобразование без существенной потери эффективности основного алгоритма.

 

4.1.5. Преобразования структур графа

 

приведем функции преобразования, которые могли бы использоваться для изменения представления графа. Так определенные функции должны, как правило, иметь доступ к структурам как исходного, так и результирующего графов, так что в соответствующих описаниях классов эти функции должны быть объявлены "друзьями" соответствующих классов. В листинге 1.13 описаны четыре функции для следующего преобразования структур: M-граф -> S-граф -> L-граф -А-граф -> M-граф.

Таким образом, с помощью этих функций можно из каждого описанного представления графа получить любое другое представление.

 

 файл convert. срр

#include "SetGraph.h"

#include "MatrixGraph.h"

#include "ListGraph.h"

#include "ArcGraph.h"

 

// Функция преобразования представления из M-графа в S-граф

SetGraph * convert(const MatrixGraph & srcGraph) {

int n = srcGraph.vertexCoun();

SetGraph *destGraph = new SetGraph(n);

for (int i = 0; i < n; i++) {

// Представление строки исходного графа:

bool * srcRow = srcGraph.graph[i];

// Соответствующее множество результирующего графа:

Set & destRow = *destGraph->graph[i];

for (int j = 0; j < n; j++) {

// Новая дуга записывается с помощью операции

// добавления элемента к множеству

if (srcRow[j]) destRow |= j; } } return destGraph;

}

// Функция преобразования представления из S-графа в L-граф

ListGraph * convert(const SetGraph & srcGraph) {

int n = srcGraph.vertexCount();

ListGraph *destGraph = new ListGraph(n);

for (int i = 0; i < n; i++) {

// Представление строки исходного графа:

Set & srcRow = *srcGraph.graph[i];

// Соответствующий список дуг в результирующем графе:

List<int> & destRow = destGraph->graph[i];

for (int j = 0; j < n; j++) {

// Обе операции - проверка принадлежности множеству и добавления

// элемента в список выполняются за фиксированное время.

 if (srcRow.has(j)) destRow.add(i);

}}

return destGraph;

}

 

// Функция преобразования представления из L-графа в А-граф.

// В этой функции используются только открытые операции А-графа,

// поэтому она может и не "дружить" с описанием класса ArcGraph

ArcGraph * convert(const ListGraph & srcGraph) {

 

int n = srcGraph.vertexCount0;

ArcGraph *destGraph = new ArcGraph(n);

 for (int i = 0; i < n; i++) {

List<int>::ListItem *current = srcGraph.graph[i].first;

while (current) {

// Добавление дуги в список дуг с помощью операции addArc.

destGraph->addArc(i, current->item);

current = current->next; } } return destGraph;

}

 

// Функция преобразования представления из А-графа в M-граф.

 MatrixGraph * convert(const ArcGraph & srcGraph) {

 int n = srcGraph.vertexCount();

MatrixGraph *destGraph = new MatrixGraph(n);

 // в цикле перебираются все дуги

for (ArcGraph::Arc * current = srcGraph.first; current; current = current->next) {

destGraph->graph[current->begin][current->end] = true;

}

return destGraph;

}

 

Обходы в графах

 

Как и в случае обхода деревьев, для графов существуют два основных класса обходов: обходы в глубину и обходы в ширину.

Обходы в глубину пытаются каждый раз после прохождения некоторой вершины А выбрать в качестве следующей такую вершину В, в которую из вершины А ведет дуга. Таким образом, алгоритмы этого класса пытаются всегда двигаться вглубь графа, находя все новые не пройденные ранее вершины. Если таких непройденных вершин нет, то алгоритм возвращается к предыдущей, ранее пройденной вершине, и пытается найти очередную дугу, ведущую из нее в какую-либо другую еще не пройденную вершину. Если и таких вершин нет, то снова происходит откат назад, и так до тех пор, пока либо все вершины не будут пройдены, либо алгоритм вернется назад в вершину, выбранную в качестве исходной.

Обходы в ширину пытаются, начав с некоторой вершины, в качестве очередных рассматривать только вершины, непосредственно связанные с исходной. Только после того, как все такие вершины будут рассмотрены, алгоритм будет пытаться рассматривать следующий слой вершин, непосредственно связанных с только что пройденными. Таким образом, алгоритм обхода в ширину последовательно рассматривает все более удаленные от исходной вершины до тех пор, пока либо все вершины не будут пройдены, либо не останется больше вершин, достижимых из исходной.

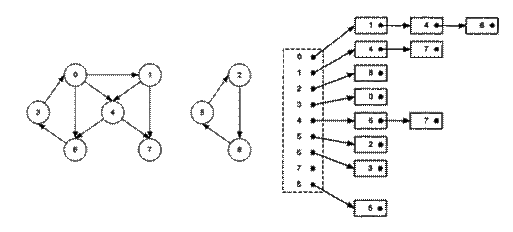
Рассмотрим в качестве примера граф, изображенный на рис. 3. Этот граф содержит 9 вершин и 12 дуг. Он состоит из двух компонент связности, так что заведомо не удастся обойти его весь, выбрав некоторую вершину в качестве исходной и проходя только по направлениям дуг. Тем не менее если сначала выбрать в качестве исходной вершины вершину 1, то все остальные вершины одной компоненты связности из нее будут достижимы, так что по крайней мере эта компонента связности будет пройдена до того, как потребуется вновь выбирать начальную вершину. Тем же свойством обладают и все остальные вершины графа, кроме вершины 7. Если выбрать ее в качестве начальной вершины для обхода, то будет пройдена только она сама, а потом потребуется вновь выбирать некоторую вершину в качестве начальной для обхода остальных.

Если в качестве алгоритма обхода взять алгоритм обхода в глубину, причем договориться, что из всех возможных альтернатив он всегда выбирает проход к вершине с наименьшим номером, то получится следующий порядок обхода вершин графа:

0; 1; 4; 6; 3; 7; 2; 8; 5

Порядок обхода в ширину в данном случае отличается от порядка обхода в глубину незначительно:

0; 1; 4; 6; 7; 3; 2; 8; 5

это получается потому, что граф, выбранный для примера, очень небольшой. Обычно в случае больших графов порядки обхода отличаются весьма существенно.

 

На рис. 3 также изображена логическая структура графа. Для того чтобы яснее представить себе работу алгоритмов обхода, необходимо хорошо представлять также и физическую структуру памяти соответствующего объекта.

В представлении графа рис. 3 в виде L-графа имеются 9 списков дуг (для каждой вершины существует список исходящих из нее дуг). На этом рисунке изображен массив списков дуг (около каждого элемента массива показан номер соответствующей вершины графа). Дуги представлены прямоугольниками, содержащими номер той вершины, в которую дуга входит.

В качестве первого примера рассмотрим внешний итератор вершин графа при обходе в глубину. Для того чтобы перейти от текущей вершины графа к следующей, итератор должен, во-первых, запоминать, какие из вершин уже пройдены или не пройдены, а во-вторых, для быстрого возврата к предыдущей вершине помнить последовательность дуг на пути из выбранной начальной вершины в текущую. Эту последовательность дуг будет удобно представляться в виде стека, элементами которого будут содержать информацию, необходимую для возврата по дугам.

Пусть алгоритм выбрал в качестве начальной вершину с номером 0. Тогда обход графа начнется в ситуации, приведенной в первой строке табл.1.

Таблица 1.

Последовательность состояний при обходе графа в глубину

Шаг	Список пройденных вершин	Текущая вершина	Стек дуг на пути к текущей вершине
1	—	0	—
2	0	1	0-1
3	0,1	4	0-1, 1-4
4	0, 1,4	6	0-1, 1-4, 4-6
5	0, 1,4,6	3	0-1, 1-4, 4-6, 6-3
6	0, 1,4, 6,3	7	0-1, 1-4, 4-7
7	0, 1,4, 6, 3,7	—	—
8	0,1,4, 6, 3,7	2	—
9	0, 1,4, 6, 3, 7,2	8	2-8
10	0, 1,4, 6, 3, 7, 2,8	5	2-8, 8-5
11	0, 1,4, 6, 3, 7,2, 8,5	—	—

 

Итератор обходит текущую вершину и выбирает следующую вершину из числа тех, в которые ведут дуги из текущей вершины. После первого шага ситуация будет такой, как показано в строке 2 табл. 1. Пройденная на этом шаге дуга 0-1 помещается в стек. Следующие три шага выполняются аналогично, а последовательное изменение ситуации показано в табл. 1 в строках 3-5.

В тот момент, когда текущей стала вершина 3, оказывается, что единственная дуга, ведущая из нее, ведет в уже пройденную вершину 0, поэтому следует, используя стек, вернуться на шаг назад в вершину 6 и попытаться найти следующую вершину по одной из дуг, ведущих из этой вершины. Поскольку новых дуг, ведущих из вершины 6, тоже больше нет, то делаем еще шаг назад к вершине 4. Теперь уже находится дуга, ведущая из этой вершины в еще не пройденную вершину 7, так что после прохода по соответствующей дуге образуется новая ситуация, показанная в табл. 1 в строке 6.

После прохождения вершины 7 оказывается, что больше нет дуг, ведущих в еще не пройденные вершины ни из вершины 7, ни из всех предыдущих вершин на пути в эту вершину. В строке 7 таблицы показана ситуация, возникшая после проверки всех этих дуг. Теперь можно снова выбрать произвольно одну из непройденных вершин, скажем, вершину 2, и далее алгоритм последовательно переберет вершины 2, 8 и 5 так, как показано в строках 8—11. Теперь все вершины графа оказываются пройденными.

Для обходов в ширину приведем два способа обхода— с помощью внешнего и внутреннего итераторов, которые, схематично описанного ниже.

Выберем произвольную вершину графа и начнем обход с этой вершины. В процессе работы алгоритма будем делить все вершины графа на три класса:

- пройденные вершины ("черные");

- вершины, которые будут пройдены на следующем шаге алгоритма ("серые");

- и все остальные непройденные вершины ("белые").

В начальный момент работы выбранная исходная вершина помещается в множество "серых" вершин, а все остальные вершины будут пока "белыми". Один шаг работы алгоритма состоит в том, что берутся все "серые" вершины, проходятся (и помещаются во множество "черных" вершин), затем находятся все "белые" вершины, в которые ведут дуги из только что пройденных вершин, и все найденные вершины перекрашиваются в серый цвет, т. е. помещаются в множество "серых" вершин.

Если "серых" вершин больше нет, то это означает, что пройдены уже все вершины, достижимые из исходной. Если при этом в графе еще остались непройденные "белые" вершины, можно снова выбрать одну из них в качестве исходной и повторить работу алгоритма.

На практике множество "серых" вершин можно организовать в виде очереди, тогда вершины из очереди можно брать по одной из головы очереди, а новые вершины, в которые ведут из нее дуги, сразу же помещать в конец очереди.