Дихотомические (бинарные) результирующие показатели и связанные с ними логит- и пробит – модели.

В классической линейной множественной регрессионной модели и в различных ее модификациях относительно зависимой переменной явно или неявно предполагалось, что она выражает количественный признак, принимая «непрерывное» множество значений. В частности, в нормальной линейной регрессионной модели предполагается, что ошибка имеет гауссовское распределение, откуда следует, что зависимая переменная у может принимать любые значения. Выделим несколько типичных ситуаций.

1) Если есть только две возможности (бинарный выбор), то результат наблюдений обычно описывается переменной, принимающей значения 0 или 1, называемой бинарной (дихотомической). В общем случае при наличии k альтернатив результат выбора можно представить переменной, принимающей значения 1,…, k. Если альтернативы нельзя естественным образом упорядочить (например выбор профессии), то их нумерация может быть произвольной. В этом случае соответствующую переменную называют номинальной.

2) Ранжированный выбор.

Как и в первом случае, есть несколько альтернатив, но они некоторым образом упорядочены. Примеры:

- доход семьи (низкий, средний, высокий, очень высокий);

- уровень образования (незаконченное среднее, среднее, среднее техническое, высшее)

Соответствующая переменная называется порядковой, ординальной или ранговой.

Для моделей с дискретными зависимыми переменными возможно формальное применение метода наименьших квадратов, однако результаты с содержательной точки зрения являются неудовлетворительными. В случае порядковых переменных интерпретация оценок коэффициентов при объясняющих переменных значительно затруднена: увеличение на единицу порядковой переменной означает переход к следующей по рангу альтернативе, однако далеко не всегда переход от первой альтернативы ко второй численно эквивалентен переходу от второй к третьей. Если же зависимая переменная является номинальной и количество альтернатив больше двух, то результаты оценивания вообще теряют смысл в силу произвольности нумерации альтернатив. Таким образом, стандартная регрессионная схема в случае номинальных эндогенных переменных нуждается в существенной коррекции.

Особый интерес вызывают модели бинарного выбора. Модели множественного выбора могут либо непосредственно сведены к моделям бинарного выбора, либо исследованы аналогичными методами.

Модели бинарного выбора

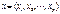Рассмотрим модель бинарного выбора на примере покупки семьей недвижимости. Будем считать, что зависимая переменная у = 1, если в течение исследуемого периода времени семья приобрела недвижимость, и у = 0 в противном случае. На решение о покупке недвижимости влияют самые различные факторы: доход семьи, количество ее членов, их возраст и др. Набор этих характеристик можно представить вектором независимых переменных. Также будем предполагать, что на решение семьи влияют также неучтенные случайные факторы (ошибки). Выдвигая различные предположения о характере зависимости у от х, будем получать разные модели. Рассмотрим линейную модель вероятности, probit -модель и logit -модель.

Линейная модель вероятности

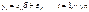Рассмотрим обычную линейную модель регрессии: ,где t – номер наблюдения (семьи),  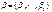– набор неизвестных параметров (коэффициентов),  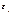– случайная ошибка. Так как 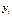принимает значения 0 или 1 и 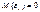, то 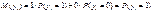. С другой стороны, по принципам регрессионного анализа 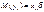. Таким образом, линейная регрессионная модель может быть записана в виде: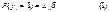

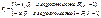Данная модель называется линейной моделью вероятности.

                              Отметим некоторые особенности этой модели, которые не позволяют успешно применять МНК для оценивания коэффициентов β:

1. Ошибка ε в каждом наблюдении может принимать только два значения Это не позволяет считать ошибку нормально распределенной или имеющей распределение, близкое к нормальному.

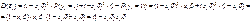2. Найдем дисперсию ошибки: Следовательно, дисперсия ошибки зависит от 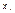, т.е. модель гетероскедастична. Как известно, оценки коэффициентов β, полученные обычным МНК, в этом случае не являются эффективными, и желательно пользоваться обобщенным МНК.

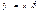3. Прогнозные значения , которые по смыслу модели есть прогнозные значения вероятности 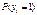, могут лежать вне отрезка [0,1] ( 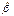 – оценка коэффициентов β, полученная с помощью обычного или обобщенного МНК), что, конечно же, не поддается разумной интерпретации.

Эти обстоятельства существенно ограничивают область применимости линейной модели вероятности. Ее целесообразно использовать при большом числе наблюдений и при достаточно точной спецификации модели, а также как инструмент первичной обработки данных.

Пробит- и логит-модели

Описание модели

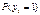Основной недостаток модели (1) в предположении о линейной зависимости вероятности от β. Его можно преодолеть, если считать, что

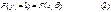где F (z) – некоторая функция, удовлетворяющая условиям: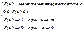

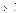В частности, в качестве F (z) можно взять функцию распределения некоторой случайной величины. Одна из возможных интерпретаций модели (2) выглядит следующим образом. Предположим, что существует некоторая количественная переменная , связанная с независимыми переменными  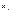обычным регрессионным уравнением 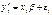, где ошибки  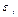независимы и одинаково распределены с нулевым средним и дисперсией 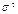. Пусть также F (z) – функция распределения нормированной случайной ошибки 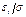. Величина  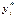является ненаблюдаемой (латентной), а решение, соответствующее значению 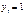, принимается тогда, когда  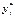превосходит некоторое пороговое значение. Так, в примере с покупкой недвижимости можно считать, что  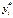представляет собой накопления семьи с номером t. Если константа включена в число регрессоров, можно считать это пороговое значение равным нулю. Таким образом, 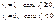Тогда, предполагая, что случайные ошибки  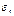имеют одно и тоже симметричное распределение F (z) (т.е. F (- z)=1- F (z)), получаем:

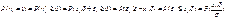, Что с точностью до нормировки совпадает с (2). Поскольку параметры β и σ участвуют только в виде отношения и не могут быть по отдельности идентифицированы, то в данном случае без ограничения общности можно считать, что σ = 1.

                              Наиболее часто в качестве функции F (z) используют:

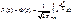· функцию стандартного нормального распределения  и соответствующую модель называют пробит-моделью

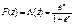· функцию логистического распределения и соответствующую модель называют логит-моделью.

В виду рассмотренной выше интерпретации модели (2) использование функции нормального распределения является достаточно естественным. Применение функции логистического распределения во многом объясняется простотой численной реализации процедуры оценивания параметров. Вопрос о том, какую из моделей (логит или пробит) следует использовать в том или ином случае, является достаточно сложным. Можно, например, выбрать ту модель, для которой больше значение соответствующей функции правдоподобия. Можно также отметить, что в окрестности нуля функции Ф(z) и Λ(z) ведут себя примерно одинаково, в тоже время «хвосты» логистического распределения значительно «тяжелее» «хвостов» нормального распределения. Практический опыт показывает, что для выборок с небольшим разбросом объясняющих переменных и при отсутствии существенного преобладания одной альтернативы над другой качественные выводы, получаемые с помощью пробит- и логит -моделей, как правило, совпадают