
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерное распределение прочности
Проиллюстрируем сравнение средней прочности волокон
а функция распределения:
Средняя прочность волокон:
Критическое эффективное напряжение
Например, из (4.2.18), (4.2.19) при При нулевой минимальной прочности
Из (4.2.19), (4.2.20) видно, что прочность пучка за счет саморазвивающегося накопления повреждений оказывается значительно ниже, чем средняя прочность волокон, и окончательное неустойчивое разрушение начинается задолго до разрушения всех волокон. Например, из условий, принятых в (4.2.20) критическое значение параметра поврежденности
Распределение Вейбулла Аналогичные оценки прочности пучка можно получить для более реального распределения Вейбулла, которое оказывается более обоснованным применительно к распределению прочности, чем называемое «нормальным» распределение Гаусса. Гипотеза Вейбулла состоит в том, что прочность материала можно рассматривать, как прочность цепи, и разрушение соответствует разрыву слабейшего звена этой цепи. Теория «слабого звена» применительно к волокнам выглядит более логичной, чем для обычных квазиоднородных сплавов, где разрушение, возникшее в одной точке (в одном элементе характерного размера), может ещё не означать разрушение всей конструкции. Обозначим P (L) вероятность разрушения волокна длины L для заданного напряжения σ. Тогда вероятность неразрушения:
В силу произвольного выбора длины L * она не зависит от L и производная от неё по L равна нулю. Получается, что производная (4.2.21) не зависит от аргумента, и, следовательно, равна константе – с, которая зависит только от приложенного напряжения и от статистических свойств прочности материала. Поэтому
Применительно к прочности волокон функцию распределения Вейбулла выбирают в следующем виде
В формуле (4.2.22) пояснён смысл функции распределения прочности для модели пучка из N волокон, n из которых разрываются при данном напряжении. Функция плотности распределения прочности получается дифференцированием (4.2.22):
Здесь и ниже для простоты принято, что минимальная прочность Распределение Вейбулла более обосновано применительно к прочности волокон, чем традиционное нормальное распределение Гаусса, которое, во-первых, «почему-то» симметрично, во-вторых, допускает бесконечно большие и отрицательные значения. Нормальное распределение имеет смысл для расчета точности артиллерийской стрельбы, когда отклонения от цели случайны и равновероятны, но для описания реальных, несимметричных, бимодальных («двугорбых») гистограмм прочности волокон его применение ничем, кроме привычки, не оправдано. Согласно гипотезе Даниэльса-Дау-Розена прочность однонаправленного композита определяется прочностью волокон нормированной эффективной длины Le (отнесенной, например, к нормирующей длине: L 0 = 1 мм). Подробнее про понятие эффективной длины – в Лекции 1.2. Теперь (4.2.22), (4.2.23) можно переписать применительно к пучку волокон конкретной эффективной длины:
Если подставить (4.2.24) в (4.2.14), то найдем критическое истинное напряжение:
где e – основание натуральных логарифмов. При исчерпании прочности пучка относительное число разрушенных волокон оказывается, естественно, меньше единицы: Средняя прочность волокон на нормированной базе испытаний
где обозначено Коэффициент реализации z прочности волокон к композите равен отношению прочности (4.2.25) пучка волокон эффективной длины к средней прочности волокон (4.2.26), определенной при испытаниях волокон с длиной
В таблице 4.2.1 приведены значения коэффициента реализации прочности Таблица 4.2.1. Коэффициент
Как видно из табл. 4.2.1, коэффициент реализации прочности волокон растёт с уменьшением эффективной длины и с ростом ширины гистограммы (рис. 4.3.1, а). Влияние роста поврежденности матрицы при длительном и циклическом нагружении на увеличение эффективной длины волокон и на снижение реализации их прочности рассмотрено в следующем разделе 4.2.4. Результаты раздела 4.2.3 поясняют, почему прочность пучка волокон за счет накопления разрывов волокон всегда ниже, чем средняя прочность волокон. Статистическая теория прочности композитов предсказывает два противоположных эффекта: рост прочности при уменьшении длины волокна (до эффективной) и снижение прочности пучка по сравнению со средней прочностью волокон. Оценки, приведенные в табл. 4.2.1, показывают, что для реальных статистических параметров прочности волокон коэффициент реализации их прочности в композите чаще бывает меньше единицы из-за влияния быстро накапливающихся разрывов волокон в пучке.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.29.143 (0.01 с.) |
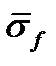 с прочностью пучка
с прочностью пучка  на примере простейшего равномерного распределения прочности между наибольшим
на примере простейшего равномерного распределения прочности между наибольшим 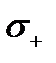 и наименьшим
и наименьшим 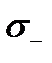 значениями. Функция плотности равномерного распределения имеет вид:
значениями. Функция плотности равномерного распределения имеет вид: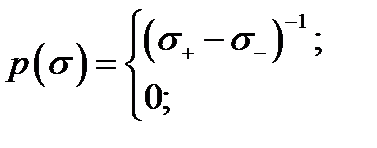

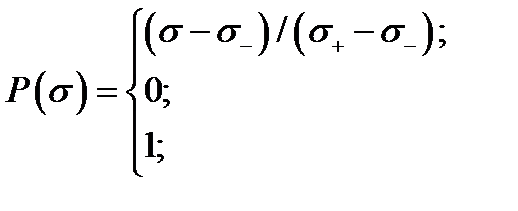


 и прочность пучка
и прочность пучка 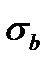 согласно (4.2.14), (4.2.15):
согласно (4.2.14), (4.2.15):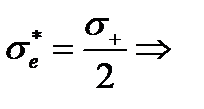
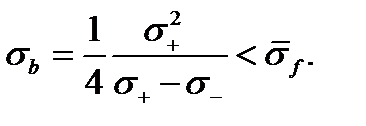
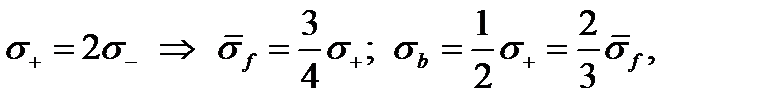 т.е. прочность пучка равна минимальной прочности и в полтора раза меньше средней прочности.
т.е. прочность пучка равна минимальной прочности и в полтора раза меньше средней прочности.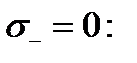

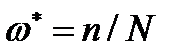 оказывается из (4.2.17) намного меньше единицы:
оказывается из (4.2.17) намного меньше единицы:
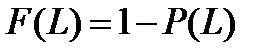 . Добавим к волокну данной длины L участок волокна произвольной длины L *. Вероятность одновременного выполнения двух независимых событий: неразрушения волокна на длине L и на длине L * выразится произведением вероятностей
. Добавим к волокну данной длины L участок волокна произвольной длины L *. Вероятность одновременного выполнения двух независимых событий: неразрушения волокна на длине L и на длине L * выразится произведением вероятностей 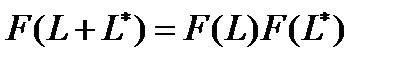 . Далее предлагается взять производную от логарифма этого произведения:
. Далее предлагается взять производную от логарифма этого произведения: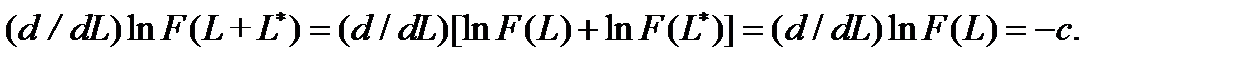 (4.2.21)
(4.2.21)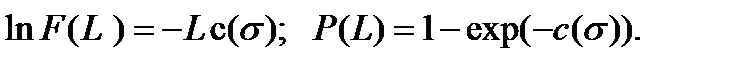 Это – основная идея.
Это – основная идея.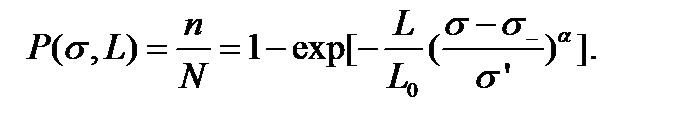 (4.2.22)
(4.2.22)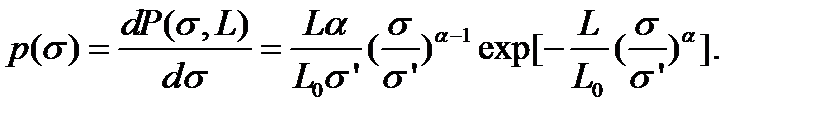 (4.2.23)
(4.2.23)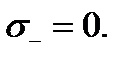
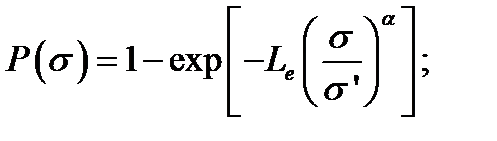
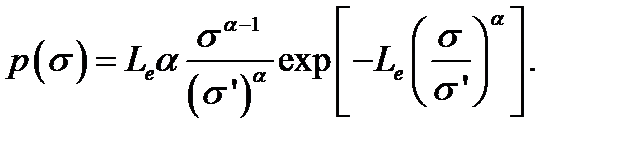
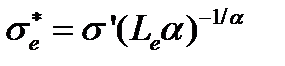 и прочность пучка волокон эффективной длины
и прочность пучка волокон эффективной длины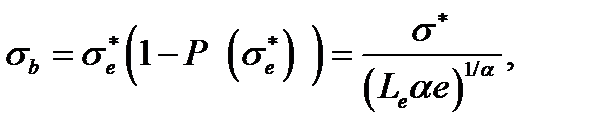
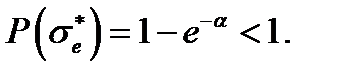 Чем больше α (чем у же гистограмма на рис. 4.2.1, а), тем ближе к единице критическое значение
Чем больше α (чем у же гистограмма на рис. 4.2.1, а), тем ближе к единице критическое значение 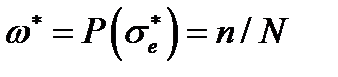 параметра поврежденности.
параметра поврежденности.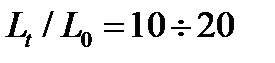 (при L 0 = 1 мм) определяется через функцию плотности распределения прочности:
(при L 0 = 1 мм) определяется через функцию плотности распределения прочности: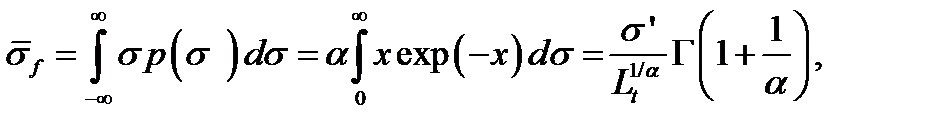
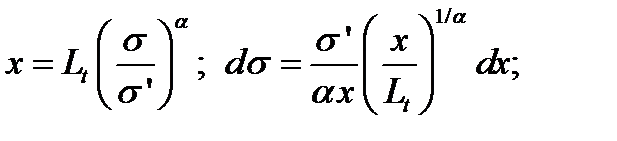 и введена табулированная гамма-функция
и введена табулированная гамма-функция 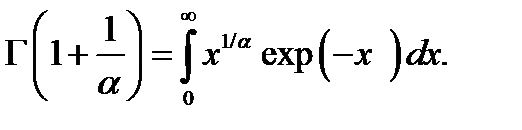
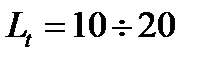 мм:
мм:
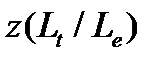 для разных отношений
для разных отношений 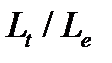 базы испытаний волокон к их эффективной длине.
базы испытаний волокон к их эффективной длине. реализации прочности волокон в однонаправленном композите в зависимости от эффективной длины
реализации прочности волокон в однонаправленном композите в зависимости от эффективной длины 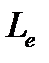 и параметра α ширины гистограммы
и параметра α ширины гистограммы


