
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрическое описание кривой в форме Фергюсона
Параметрическое представление пространственной кривой имеет следующий вид: x = x (u); y = y (u); z = z (u), (2.10) где u – параметр (u Î I, где I – интервал описания). Каждому значению параметра u соответствует одно значение зависимых переменных. При этом каждая переменная изменяется независимо от других. Выбор системы координат не влияет на форму кривой. Для описания кривых обычно используются методы кусочно-линейной аппроксимации полиномами, заданными в параметрической форме. При выборе конкретного метода из множества возможных необходимо выполнить ряд требований: · Методы должны обеспечивать гладкое соединение отдельных кривых. · Методы должны обеспечивать возможность управления формой кривой путём изменения небольшого количества параметров. · Включение нового сегмента кривой не должно нарушать гладкость всей кривой. Перечисленным требованиям удовлетворяет, например, кривая в форме Фергюсона. Плоская кривая в этой форме описывается уравнением вида: P (u) = mu 3 + nu 2 + pu + q, (2.11) где u – параметр; m, n, p, q – постоянные коэффициенты. Значения коэффициентов определяются из следующих предположений: · значение параметра u в начальной точке кривой равно 0; а в конечной точке равно 1; · известны координаты граничных точек кривой P(0) и P(1), а также значения производной в этих точках. С учётом этих предположений величины m, n, p, q находятся из решения следующей системы уравнений:
Решив эту систему, получаем значения параметров аппроксимации: m = 2 (A – B) + C + D; n = 3 (B – A) – 2 C – D; p = C; q = A. (2.13) Параметрическая кривая, заданная в форме Фергюсона, имеет следующие свойства: · Кривая полностью определена условиями, заданными в граничных точках. · Касательные к кривой, проведенные в граничных точках, параллельны векторам производной. Поэтому возможно гладкое соединение сегментов кривых, если равны координаты их граничных точек. · Изменение модулей векторов производных приводит к изменению формы кривой. Применение кубических сплайн-функций. Функция, которая составлена из полиномов k -й степени, и в узлах является (k -1) раз непрерывно дифференцируемой, называется сплайн-функцией.
Если заданы также опорные точки, через которые проходит кривая, описываемая этой функцией, то она называется интерполирующей сплайн-функцией или сплайном. Функция Q (u) называется кубическим сплайном, если она удовлетворяет следующим условиям: 1. Задан упорядоченный набор из n +1 точек u 0,…, un (узлы сплайна) и соответствующие этим узлам опорные точки S 0,…, Sn. 2. На каждом интервале (uk, uk –1) для k = 0, 1, 2,…(n – 1) функция Q (u) является кубическим полиномом: fk (u), k =3, т.е.: fk (u) = Ak (u – uk)3 + Bk (u – uk)2 + Ck (u – uk) + Dk. 3. В узлах u 0,…, un функция Q (u) принимает заданные значения S 0,... Sn: Q (uk) = Sk, k = 0, 1, 2,… n. 4. На всём интервале, включая и узлы, Q (u) должна быть дважды непрерывно дифференцируемой функцией: fk ¢(uk) = fk +1¢(uk), fk ¢¢(uk)= fk +1¢¢(uk). 5. Заданы значения первых производных в граничных точках u 0 и un или значения первых двух производных в граничной точке u 0. Преимущества кубических сплайнов: –Удобство использования, так как для построения кривой необходимы только значения сплайн-функции в узлах (опорные точки) и значения первых производных в концевых точках. – На каждом интервале кривая определяется кубическим полиномом. – Так как кривая на всем интервале дважды непрерывно дифференцируема, то у неё нет точек перегиба.
Пример применения метода аппроксимации при формировании оптимальной траектории полета БЛА В качестве примера практического применения метода аппроксимации рассмотрим построение оптимальной траектории полета БЛА класса «поверхность-воздух». Основное требование к оптимальной траектории – распределение перегрузок по траектории должно обеспечивать минимум сопротивления, а, следовательно, и запаса топлива. Принято, что расчетная траектория располагается в вертикальной плоскости, проходя через точку старта и упрежденную точку встречи, и строится в опорной системе координат, у которой ось OX направлена из точки старта в упрежденную точку встречи, ось OY ей перпендикулярна, ось OZ горизонтальна (рис. 2.1). Для аналитического описания траектории в опорной системе координат воспользуемся упрощенным выражением аппроксимирующей зависимости приведенной в работе [17]:
Здесь обозначено где x, y – координаты БЛА в опорной системе координат, r т.в – дальность до упрежденной точки встречи; А i, – варьируемые коэффициенты, n – заданная степень ряда.
Рис. 2.1. Опорная траектория ЗУР Отметим попутно, что траектория БЛА в земной системе координат определяется следующим выражением:
где ɛт.в – угол места в точке встречи, H – высота полета цели, x Г – горизонтальная дальность полета. Выражения для нормированных значений первой и второй производных, необходимые для определения параметров траектории имеют вид:
Траектория полета БЛА в форме (2.14) отвечает следующим граничным условиям: при при Основными параметрами траектории являются: углы наклона траектории в точке старта ϴст и в точке встречи ϴт.в, а также перегрузка в точке встречи. Угол наклона траектории в точке встречи определяется выражением: ϴт.в = ɛт.в + φт.в (2.17) где: φт.в – угол наклона траектории в точке встречи в опорной системе координат определяется через первую производную φт . в = arctg Для обеспечения минимального индуктивного сопротивления по траектории потребную перегрузку в точке встречи (при Потребная перегрузка по траектории включает маневренную составляющую (центростремительная сила, деленная на вес), определяемую через текущую кривизну траектории ρ, и гравитационную составляющую
Откуда выражение для потребной нормальной перегрузки запишем в виде: ny = V 2 /(g ρ) + cosϴ, (2.21) В формуле потребной нормальной перегрузки текущая кривизна траектории определяется через вторую производную:
Тогда окончательно выражение для потребной нормальной перегрузки будет иметь вид: ny = Подставляя в (2.16)
В большинстве случаев опорные траектории описываются полиномом 3-го, 4-го порядка (n =2–3). Так, например, при n =2 выражение (2.14) преобразуется к виду:
При условии А1=А2 опорная траектория описывается полиномом: Тогда выражения для первой и второй производных преобразуются к виду:
Рассмотрим граничные условия: при при
Полученная траектория (2.27) характеризуется тем, что при малых углах подхода к цели ее кривизна и потребная перегрузка (без учета составляющей веса), исходя из (2.24), (2.28) изменяются практически линейно, уменьшаясь до нуля в точке встречи. Значение коэффициента А1 = – Если в качестве примера задать значение
Основное требование к оптимальной траектории – обеспечивать минимум сопротивления – реализуется распределением потребных перегрузок по опорной траектории. Оно может быть получено из соотношений (2.23) и (2.16). При известных по траектории значениях скорости V, параметров Ai, высоты Нт.в и дальности до точки встречи r т.в процедура определения ny (t) не вызывает затруднений. Это связано с тем, что опорная траектория задана в виде нормированного полинома с постоянными коэффициентами Ai. При этом кривизна траектории ρ определяется как функция 1-ой и 2-ой производных от опорной траектории, которые, в свою очередь, определяются нормированными полиномами с теми же коэффициентами Ai. Таким образом, аналитическое выражение для траектории полета БЛА в форме (2.14) удовлетворяет требованиям обеспечения минимума сопротивления, а, следовательно, и запаса топлива.
|
|||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.177 (0.03 с.) |
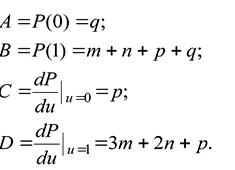 (2.12)
(2.12)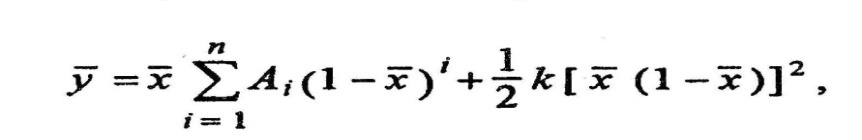 (2.14)
(2.14)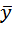 = y / r т.в,
= y / r т.в, 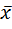 = x / r т.в,
= x / r т.в,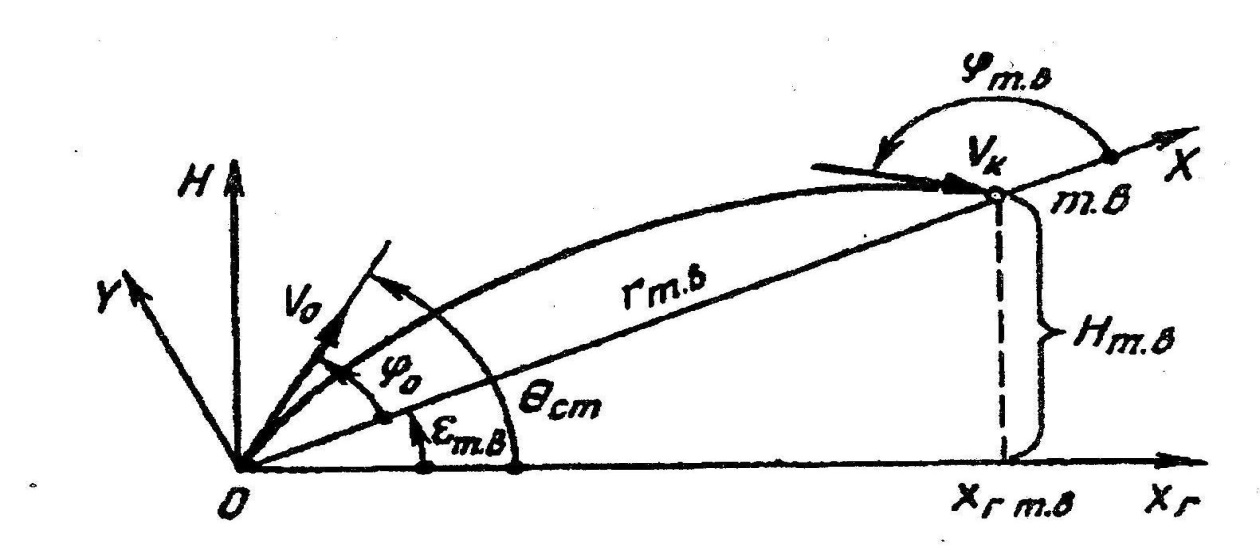
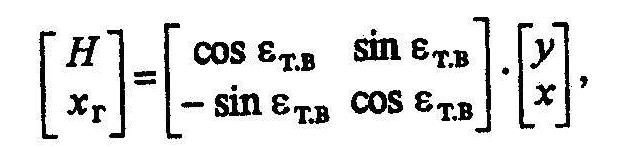 (2.15)
(2.15)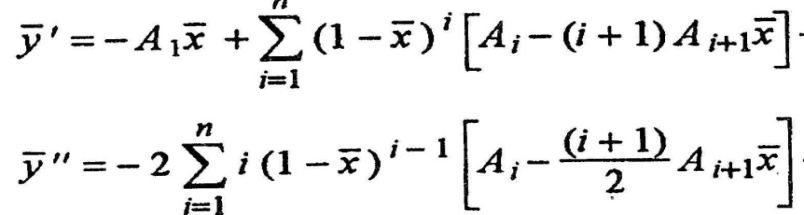 (2.16)
(2.16) =arctg
=arctg 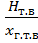 (2.18)
(2.18)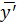 при
при 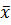 =1:
=1: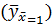 = – arctg(A1) (2.19)
= – arctg(A1) (2.19)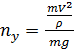 +
+ 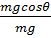 (2.20)
(2.20)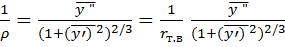 (2.22)
(2.22)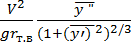 + cosϴ (2.23)
+ cosϴ (2.23) ꞌ= – A 1; (2.24)
ꞌ= – A 1; (2.24)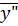 = – 2(A 1 – A 2). (2.25)
= – 2(A 1 – A 2). (2.25)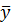 =
= 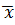 (A 1 (1–
(A 1 (1– 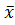 2 +(A 1 + A 2)
2 +(A 1 + A 2) 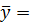 A 1
A 1 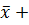 2)
2)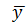 ꞌ= 2А1;
ꞌ= 2А1; 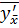 =1 могут быть определены (см. 2.19) путем задания желаемого угла наклона траектории в точке встречи в опорной системе координат φт.в. Рекомендуемое в работе [21] значение
=1 могут быть определены (см. 2.19) путем задания желаемого угла наклона траектории в точке встречи в опорной системе координат φт.в. Рекомендуемое в работе [21] значение 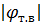 ˂ 35º.
˂ 35º.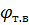 = –30º. Тогда А1 = 0,578 и аналитическое описание траектории ЗУР в опорной системе координат примет вид:
= –30º. Тогда А1 = 0,578 и аналитическое описание траектории ЗУР в опорной системе координат примет вид:


