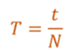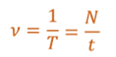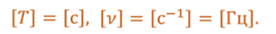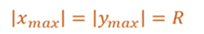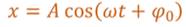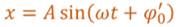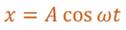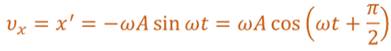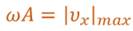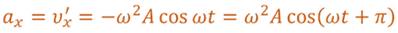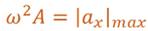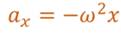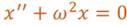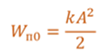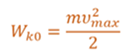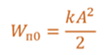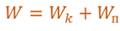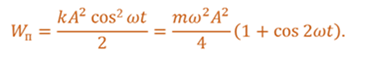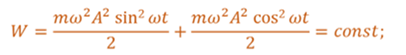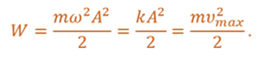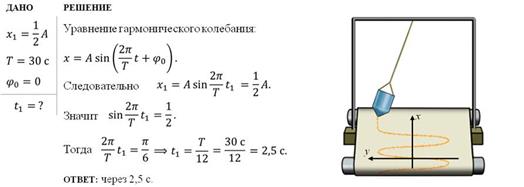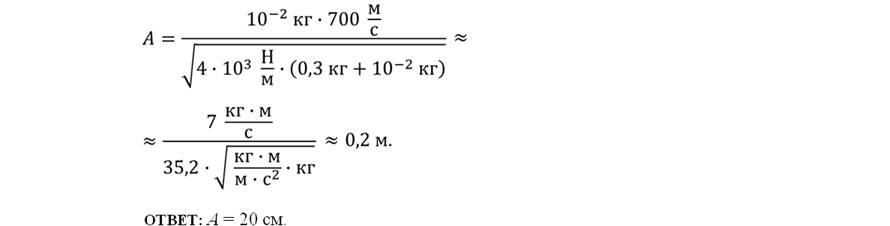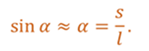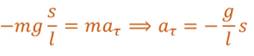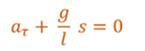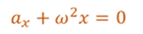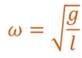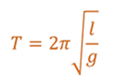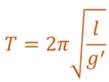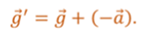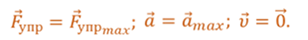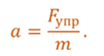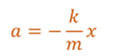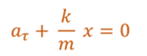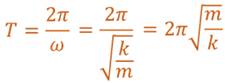Внимательно прочитайте и посмотрите лекцию, составьте конспект

 

1. Колебания бывают двух типов: свободные и вынужденные. Свободные колебания возникают за счет внутренних сил системы, после того как она была выведена из состояния равновесия. Вынужденные колебания возникают за счет внешней периодической силы.

Самым простым колебательным движением тела является гармоническое колебание. Гармоническим называют колебание, в процессе которого величины, характеризующие движение (смещение, скорость, ускорение и др.), изменяются по закону синуса или косинуса (гармоническому закону). В общем виде этот закон задается формулой:

x(t)=Asin(ωt+φ0),

где x(t) — значение изменяющейся величины в момент времени t, A — амплитуда колебаний, ω — циклическая (круговая) частота колебаний, φ0 — начальная фаза колебаний.

Гармонические колебания являются периодическими. Период T этих колебаний равен периоду функции sin(ωt+φ0), то есть

T=2πω.

Очень часто как свободные, так и вынужденные колебания в различных механических колебательных системах имеют форму гармонических колебаний. Поведение тела, совершающего колебания по гармоническому закону, описывается дифференциальным уравнением вида

x″+ω2x=0,

где x″ — вторая производная координаты x тела по времени t, то есть проекция ax его ускорения на ось x.

 

2.Окружающий нас мир наполнен разнообразными колебательными дви­жениями и процессами: колеблются ветки деревьев и кузов автобуса при движении. Колебания струн под руками умелого музыканта вызывают колебания воздуха, и слышится прекрасная музыка.

Кроме того, многие важнейшие процессы внутри организма человека явля­ются колебательными: сердце человека в спокойном состоянии совершает око­ло одного колебательного движения в секунду, под действием повторяющихся нервных импульсов каждая мышца в теле человека непрерывно то сокращается, то растягивается.

Таким образом, колебанием называется процесс, при котором какая-либо физическая величина, характеризующая этот процесс, последовательно изменяется то в одну, то в другую сторону около некоторого своего среднего значения. Например, на качелях, подвешенных на веревках, человек отклоняется то вперед и вверх, то назад и вверх от положения равновесия. Говорят, что качели являются колебательной системой.

Таким образом, механической колебательной системой называется совокупность тел, в которой могут происходить колебательные процессы.

Наиболее простыми механическими колебательными системами являются: вертикаль­ный пружинный маятник, который образуют Земля, штатив, пружина и груз; физический маятник, образованный Землей, штативом и шариком на нити; и горизонтальный пружинный маятник — это два штатива, две пружи­ны и шарик.

Колебательный процесс в системе может происходить под действием как внутренних, так и внешних сил. Если колебания в системе происходят только под действием внутренних сил, то их называют свободными колебаниями.

А если колебания тела повторяются через определен­ный промежуток времени, то их называют периодическими.

Рассмотрим условия, которые необходимы для того, чтобы в системе могли возникнуть свободные колебания:

1) Необходимо наличие положения устойчивого равновесия.

2) Необходимо наличие у тела избыточной механической энергии по сравнению с ее энергией в положении устойчивого равновесия, так как самопроизвольно (то есть без внешнего воздействия) система не может выйти из положения равновесия.

3) на тело должна действовать возвращающая сила, то есть сила, всегда направленная к положению устойчивого равновесия.

4) В идеальных колебательных системах должны отсутствовать силы сопротивления.

Теперь рассмотрим некоторые важные характеристики колебательного движения.

Периодом колебания называется промежуток времени, в течение которого совершается одно полное колебание.

Частота колебаний — это величина, об­ратная периоду, равная числу колебаний, совершенных системой за одну секунду.

В СИ период измеряется в секундах, а частота — в герцах.

Смещением называется любое откло­нение физической величины от ее значе­ния в положении равновесия и измеряемая расстоянием от положения равновесия до положения точки в заданный момент времени.

Амплитудой называется максималь­ное смещение тела от положения равновесия.

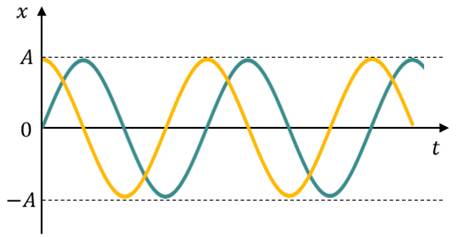
Простейшим видом колебаний являются гармонические колебания. Термин «гармонические колебания» впервые был введен в науку швейцарским физиком Даниилом Бернулли. Гармоническими называются колебания, при которых какая-либо величина изменяется с тече­нием времени по закону синуса или косинуса.

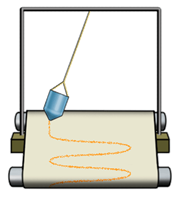
Например, гармонические колебания фи­зического маятника можно зарегистрировать следующим способом. В качестве груза взять небольшой стакан с песком, который мо­жет высыпаться через очень маленькое отверстие снизу.

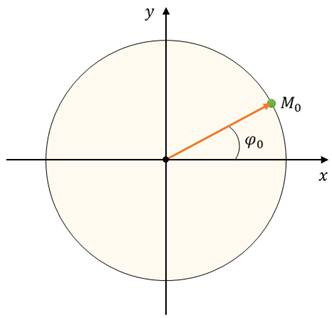
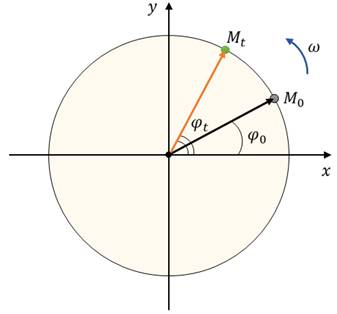
Если под колеблющимся маятником двигать равномерно по столу бумажную ленту, то полученная на бумаге кри­вая представляет собой синусоиду или косинусоиду в зависи­мости от выбора начального момента времени наблюдения (момента отсчета времени).

Чтобы установить основные кинематические признаки гармонических коле­баний, рассмотрим их математическую модель на примере изменения физичес­ких величин, характеризующих движение материальной точки по окружности с постоянной угловой скоростью. Начало координат поместим в центре окружности радиуса R. Пусть в начальный момент времени материальная точка находилась в положении M ₀ и ее радиус-вектор составлял с осью Ox угол j ₀.

Через промежуток времени t точка переместится в положение M, а ее радиус-вектор при этом повернется на угол D j и составляет в данный момент с осью Ox угол

Запишем теперь координаты точки в этот момент времени

Теперь расположим перпендикулярно друг к другу два экрана и будем освещать движущийся шарик. На вер­тикальном экране тень от шарика будет двигаться вдоль оси Oy по закону:

То есть совершать колебания возле начала координат. На горизонтальном экране тень шарика будет двигаться вдоль оси Ox по закону:

И также совершать колебания около начала координат.

Величина, стоящая под аргументом синуса или косинуса, или, в вы­бранной системе отсчета, угол между радиус-вектором и осью абсцисс называется фазой колебания.

Начальная фаза колебания j ₀ характеризует положение точки в началь­ный момент времени.

Тогда мгновенные значения координат x и y, можно рассматри­вать как смещения шарика от нулевого значения, а модуль амплитудного значения для обеих координат равен радиусу окружности.

Таким образом, кинематический закон любого гармонического движения можно представить в виде:

Следовательно, графически зависимость смещения колеблющейся точки от времени изображается косинусоидой или синусоидой.

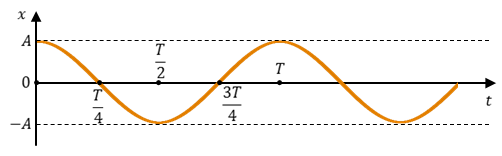
В записанных уравнениях w — это циклическая (или круговая) частота, которая показывает, сколько колебаний совершает материальная точка за 2 p секунд. Соответственно, в системе СИ она измеряется в радианах на секунду.

Рассмотрим, как изменяются проекции скорости и ускорения колеблющейся точки со временем для случая, когда начальная фаза колебаний равна нулю.

Начнем со скорости. Для этого найдем первую производную по времени от кинематического закона гармонических колебаний.

В полученном выражении произведение циклической частоты и амплитуды колебаний — это есть амплитуда проекции скорости на ось координат.

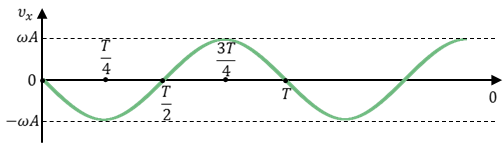
Таким образом видим, что при гармонических колебаниях проекция скорости тела на координатную ось тоже изменяется по гармоническому закону с той же частотой, но с другой амплитудой и опережает по фазе смещение на p /2.

Теперь рассмотрим ускорение. Для этого найдем производную от проекции скорости по времени.

Величина, равная произведению квадрата циклической частоты и амплитуды колебаний, является амплитудой проекции ускорения.

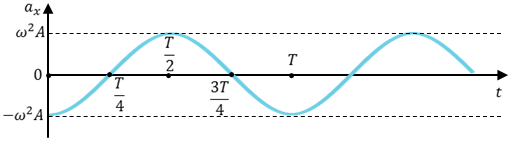
Как видно из формулы, при гармонических колебаниях проекция ускорения опережает смещение по фазе на p. Говорят, что проекция ускорения изме­няется с течением времени в противофазе изменению координаты.

Учитывая кинематический закон гармонического движения получим, что при гармонических колебаниях проекция ускорения прямо пропорциональна смещению и противоположна ему по знаку, то есть направлено в сторону, противоположную смещению.

Так как проекция ускорения — это вторая производная от смещения по времени, то последнее соотношение можно записать в виде:

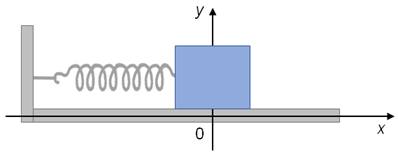
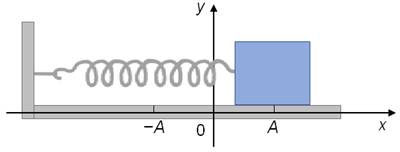
Это уравнение называется уравнением гармонических колебаний.

Рассмотрим процесс превращения энергии при гармонических колебаниях на примере идеального горизонтального пруженного маятника. Горизонтальный уровень, на котором находится маятник, выбираем за нулевой уровень отсчета потенциальной энергии маятника в поле силы тяжести.

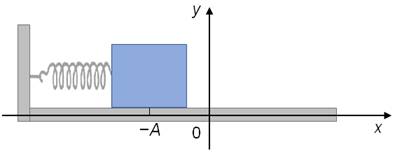
Если вывести тело из положения равновесия, например, сжав пружину на некоторую величину, то сообщается этому телу некоторый запас потенциальной энергии.

После прекращения внешнего воздействия, тело придет в движение. При движении к положению равновесия его потенциальная энергия убывает, а кинетическая наоборот, возрастает, так как деформация пружины уменьшается, а скорость движения тела увеличивается. В момент прохождения телом положения равновесия его потенциальная энергия равна нулю, а вот кинетическая энергия будет максимальна.

После прохождения положения равновесия скорость тела начинает уменьшаться, а пружина растягивается. Следовательно, кинетическая энергия тела начинает убывать, а потенциальная наоборот — возрастать. В точке максимального отклонения тела его кинетическая энергия равна нулю, а потенциальная — максимальна.

Таким образом, при колебаниях периодически происходит переход потенциальной энергии в кинетическую и обратно.

Полная механическая энергия такой колебательной системы равна сумме его кинетической и потенциальной энергий.

Если смещение материальной точки, совершающей колебания, изменяется с течением времени по гармоническому закону, то, как известно, и скорость тела изменяется также по гармоническому закону. Следовательно, кинетическую и потенциальную энергию колеблющегося тела можно задать следующими функциями

Из этих формул видно, что кинетическая и потенциальная энергии изменяются тоже по гармоническому закону, с одинаковой амплитудой и в противофазе друг с другом.

А вот полная механическая энергия системы, равная сумме кинетической энергии тела и упругой энергии пружины, остается неизменной и равной начальной максимальной потенциальной энергии, либо его кинетической энергии в момент прохождения положения равновесия.

В реальных условиях на маятник всегда действуют силы сопротивления, поэтому полная энергия уменьшается, и свободные колебания маятника с течением времени затухают, то есть их амплитуда уменьшается до нуля. Такие колебания называются затухающими.

Основные выводы:

Рассмотрели, какое движение называется колебательным и что называют свободными колебаниями. Повторили основные характеристики колебательного движения. Вспомнили, какие колебания называются гармоническими и рассмотрели, какие превращения энергии происходят при гармонических колебаниях.

Посмотрите https://www.youtube.com/watch?v=W806HMmhVXE

Задачи

Через какой минимальный промежуток времени после начала колебаний смещение точки из положения равновесия будет равно половине амплитуды, если период колебаний 30 с, а начальная фаза равна нулю?

Задача 4. Тело массой 20 г совершает гармонические колебания с амплитудой 5 см и частотой 20 Гц. Определите полную энергию колебаний, а также мгновенные значения проекций скорости и ускорения и координаты тела, если в начальный момент времени оно находилось в положении равновесия.

Задача 5. На гладком горизонтальном столе лежит шар массой 300 г, прикрепленный к пружине жесткостью 4 кН/м. Пуля массой 10 г, летящая горизонтально со скоростью 700 м/с, попадает в шар и застревает в нем. Определите амплитуду колебаний шара с пулей. Сопротивлением воздуха и массой пружины можно пренебречь.

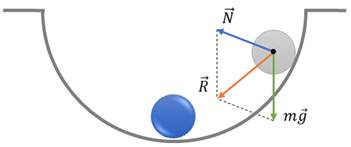
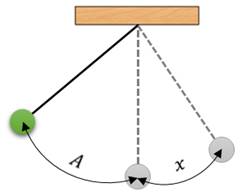
3 посмотрите https://www.youtube.com/watch?v=hbqmuXL6kg4

Рассмотрим для начала математический маятник. Математическим маятником называется находящаяся в гравитационном поле материальная точка, подвешенная на невесомой и нерастяжимой нити, прикрепленной к подвесу. Математический маятник — это модель малых реальных колебаний тела под действием силы тяготения при условии, что можно пренебречь:

1) размерами подвешенного тела, по сравнению с длиной нити;

2) сопротивлением движению тела;

3) массой нити и ее деформацией.

Рассмотрим подробно колебания математического маятника в инерциальной системе отсчета, относительно которой точка его подвеса движется прямолинейно и равномерно или же покоится. И так, пусть в начальный момент времени маятник покоится в положении равновесия. Тогда, действующие на маятник сила упругости нити и сила тяжести материальной точки взаимно компенсируются.

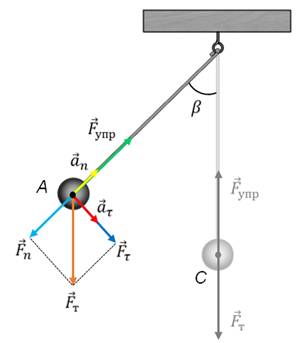
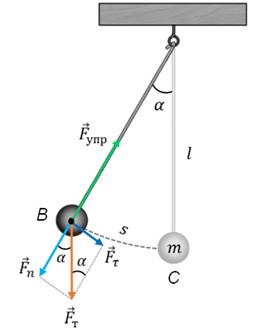
Теперь отклоним маятник на некоторое расстояние от точки равновесия и отпустим его. В этом случае, сила тяжести и сила упругости нити уже не будут компенсировать друг друга. Разложим вектор силы тяжести на две составляющих — тангенциальную и нормальную.

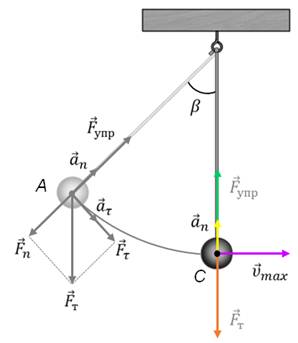
Как видим, тангенциальная составляющая силы тяжести направлена к положению равновесия, то есть она является возвращающей силой. При этом она сообщает материальной точке тангенциальное ускорение и маятник начнет двигаться к положению равновесия с возрастающей по модулю скоростью. А нормальная составляющая силы тяжести, как видно из рисунка, направлена вдоль нити против силы упругости. Их равнодействующая сообщает маятнику нормальное ускорение, которое изменяет направление вектора скорости. В результате маятник начинает двигаться по дуге.

Чем ближе маятник будет подходить к положению равновесия, тем меньше становиться значение возвращающей силы и тем больше становиться скорость движения маятника. Дойдя до положения равновесия, возвращающая сила становится равной нулю.

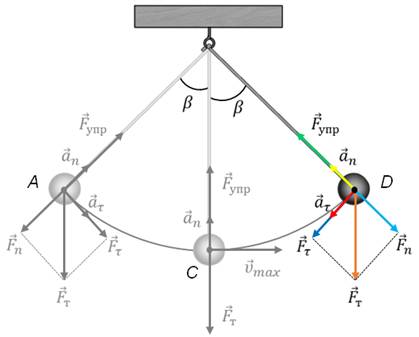
При этом скорость движения маятника достигает своего максимума и, не останавливаясь, маятник продолжает свое движение дальше уже по инерции, поднимаясь по дуге вверх. При этом вновь возникает возвращающая сила, которая становится тем больше, чем выше поднимается маятник. Но так как возвращающая сила теперь направлена против движения маятника, то его скорость убывает и в точке D скорость маятника становится равной нулю.

Маятник на мгновение останавливается, а затем начинает двигаться в обратном направлении к положению равновесия. Опять пройдя его по инерции, маятник, замедляя свое движение, дойдет до точки А, тем самым совершив одно полное колебание. А так как силы сопротивления отсутствуют, то после этого движение маятника будет повторяться в уже описанной последовательности.

Получим уравнение, описывающее свободные колебания математического маятника. Пусть маятник в данный момент времени находится в точке B.

Его смещение от положения равновесия в этот момент равно длине дуги CB.

Пусть длина нити подвеса маятника равна l, а его масса m. Из рисунка видно, что значение возвращающей силы (то есть тангенциальной составляющей силы тяжести), можно найти как произведение модуля силы тяжести на синус угла отклонения маятника от вертикали.

Из геометрии известно, что по определению синус острого угла есть отношение противолежащего катета к гипотенузе. Также из геометрии известно, что при малых углах (то есть когда острый угол меньше десяти градусов) синус угла можно заменить его градусной мерой.

Перепишем уравнение для тангенциальной составляющей силы тяжести с учетом последнего равенства.

Обратите внимание на знак «минус» в этой формуле. Его здесь ставят потому, что тангенциальная составляющая силы тяжести направлена к положению равновесия, а смещение отсчитывают от положения равновесия. Теперь применим второй закон Ньютона для нашего маятника, в проекциях на направление касательной к траектории движения математического маятника.

Таким образом, имеются два уравнения, в которых равны их левые части. А раз равны левые, то и правые части этих равенств также должны быть равными. Сократив полученное равенство на массу маятника, приходим к тому, что тангенциальное ускорение математического маятника прямо пропорционально его смещению и направлено к положению равновесия.

Эту формулу называют динамическим уравнением движения математического маятника.

Теперь перепишем это уравнение следующим образом

А теперь сравним его с уравнением гармонических колебаний.

Из такой записи видно, что колебания математического маятника являются гармоническими. А так как рассмотренные колебания происходили только под действием внутренних сил, то это были свободные колебания. Таким образом, можно сделать важный вывод о том, что при малых углах отклонения свободные колебания математического маятника являются гармоническими.

Также из анализа формул следует, что циклическая частота колебаний маятника равна квадратному корню из отношения ускорения свободного падения к длине маятника.

Помня о том, что период колебаний и циклическая частота связаны друг с другом обратной пропорциональностью, получим формулу, по которой можно рассчитать период свободных колебаний математического маятника.

Полученная формула называется формулой Гюйгенса, так впервые была получена нидерландским физиком Христианом Гюйгенсом.

Следует обратить внимание на то, что эту формулу можно использовать для расчета периода при выполнении одновременно двух условий:

1) колебания маятника должны быть малыми, так как эта формула дает результаты приемлемой точности (ошибка менее одного процента) при углах, не превышающих 4º;

2) точка подвеса маятника должна покоиться или двигаться прямолинейно и равномерно относительно инерциальной системы отсчета, в которой находится маятник.

Дело в том, что если точка подвеса математического маятника движется с некоторым ускорением, то изменяется сила натяжения нити. Это приводит к изменению возвращающей силы, а, следовательно, частоты и периода колебаний. В этом случае в формуле периода математического маятника ускорение свободного падения следует заменить на так называемое «эффективное» ускорение маятника в неинерциальной системе отсчета.

«Эффективное» ускорение можно найти, как векторную сумму ускорения свободного падения и вектора, противоположного вектору ускорения, с которым движется маятник.

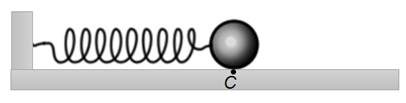
Теперь рассмотрим колебания пружинного маятника. Пружинным маятником называется система, состоящая из пружины жесткостью k и материальной точки массой m.

В простейшей модели пружинного маятника рассматривают только упругую деформацию пружины и пренебрегают:

1) любыми силами сопротивления;

2) размерами тела, то есть тело принимают за материальную точку;

3) массой пружины.

Различают два вида пружинных маятников — горизонтальный и вертикальный.

В горизонтальном пружинном маятнике, колебания тела происходят вдоль горизонтальной прямой.

У вертикального пружинного маятника колебания происходят вдоль вертикальной прямой.

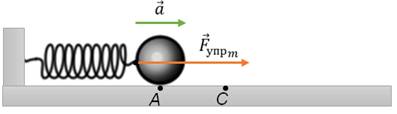
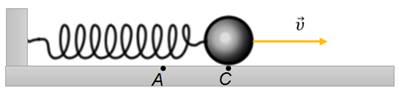
Рассмотрим более подробно колебания идеального горизонтального пружинного маятника. Пусть в начальный момент времени пружина не деформирована, и тело находится в положении равновесия.

Теперь выведем тело из положения равновесия, например, сжав пружину на некоторую величину, и отпустим его. И так, со стороны деформированной пружины на тело начнет действовать сила упругости, которая всегда будет направленна к положению равновесия, и под действием этой силы тело начнет ускоренно двигаться. При этом в самом крайнем положении на тело действует максимальная сила упругости, так как здесь абсолютное удлинение пружины наибольшее. Значит и ускорение тела в этом положении максимальное.

При движении тела к положению равновесия абсолютное удлинение пружины начинает уменьшаться, а, следовательно, уменьшается и ускорение, сообщаемое силой упругости. Но так как ускорение сонаправлено со скоростью, то скорость маятника увеличивается и в положении равновесия, как и в случае с математическим маятником, она будет максимальна.

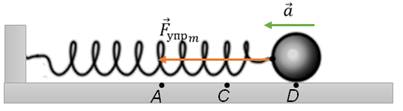
Достигнув положения равновесия, тело не остановится (хотя в этом положении пружина не деформирована), а будет по инерции двигаться дальше, растягивая пружину. Возникающая при этом сила упругости направлена теперь против движения тела и тормозит его. В точке D тело на мгновение остановится, так как его скорость окажется равной нулю. Но ускорение в этой точке максимально, так как максимальна действующая сила упругости и под действием этой силы тело начнет двигаться в обратную сторону, к положению равновесия.

Вновь пройдя его по инерции, тело, сжимая пружину и замедляя движение, дойдет до точки A, то есть совершит одно полное колебание. После этого движение маятника будет повторяться в описанной последовательности.

Таким образом, причинами свободных колебаний пружинного маятника являются действие силы упругости, возникающей при деформации пружины, и инертность тела.

Получим уравнение, описывающее движение пружинного маятника. И так, согласно второму закону Ньютона, единственный результат действия силы упругости — это сообщение телу ускорения.

По закону Гука, сила упругости прямо пропорциональна смещению тела и противоположно ему направлена.

Перепишем второй закон Ньютона с учетом определения силы упругости пружины.

Как видно из уравнения, ускорение маятника прямо пропорционально смещению и противоположно ему по направлению.

Перепишем уравнение следующим образом

Полученное равенство является динамическим уравнением движения пружинного маятника.

Сравнивая его с уравнением гармонических колебаний, видим, что пружинный маятник совершает гармонические колебания с циклической частотой равной

Учитывая, что период колебаний и циклическая частота связаны друг с другом обратной пропорциональностью, получим формулу, по которой можно рассчитать период свободных колебаний пружинного маятника.

По этой же формуле можно рассчитывать и период колебаний вертикальногопружинногомаятника.

Основные выводы:

Рассмотрели математический и пружинный маятники. Рассмотрели условия возникновения свободных гармонических колебаний в таких системах. А также вспомнили формулы, по которым можно рассчитать период свободных колебаний математического и пружинного маятников.

 

Домашнее задание

Конспект выцчить

Решить задачу

 

Самый высокогорный город мира — маленький перуанский шахтёрский городок Серро-де-Паско, расположенный в Центральных Андах на высоте 4380 метров над уровнем моря. На сколько будут отставать маятниковые часы за сутки, выверенные на уровне моря, если их поднять на эту высоту? Принять маятник в часах за математический, а R _з = 6370 км.

Домашнее задание и лекцию сфотографировать или скан и прислать на почту helen. mails @ mail. ru