
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Производная функции.
Понятие производной. Пусть функция Определение 8.1. Производной функции
Производная функции имеет несколько обозначений: Пример 8.1. Используя определение, доказать, что Решение: Найдем приращение функции
Тогда Определение 8.2. Операция отыскания производной данной функции называется дифференцированием этой функции. Определение 8.3. Функция, имеющая в точке Основные правила дифференцирования. 1) Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
2) Производная произведения двух дифференцируемых функций равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый:
3) Производная частного двух дифференцируемых функций может быть найдена по формуле:
4) Постоянный множитель можно выносить за знак производной:
Таблица производных.
Пример 8.2. Найти производную функции Решение: Используя правила дифференцирования (1 и 4) и таблицу производных, находим, что
Пример 8.3. Найти производную функции Решение: Используя правило дифференцирования (2) и таблицу производных, находим, что
Пример 8.4. Найти производную функции Решение: Используя правило дифференцирования (3) и таблицу производных, находим, что
Производная сложной функции. Пусть
Теорема 8.1. Если
Пример 8.5. Найти производную функции Решение: Исходную функцию можно представить в виде 1) 2) 3) Следовательно,
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 35; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.228.95 (0.005 с.) |
 определена на интервале
определена на интервале 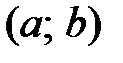 . Выберем произвольную точку
. Выберем произвольную точку  из этого интервала и зададим значению
из этого интервала и зададим значению  приращение
приращение  . Тогда функция получит соответствующее ему приращение
. Тогда функция получит соответствующее ему приращение 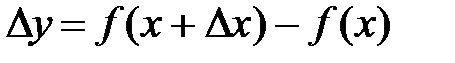 .
.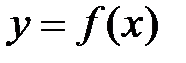 в точке
в точке 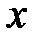 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует), т.е.
называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует), т.е. .
. .
. .
. в точке
в точке  .
. , где
, где  при
при 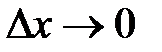 (попервому замечательному пределу),
(попервому замечательному пределу), 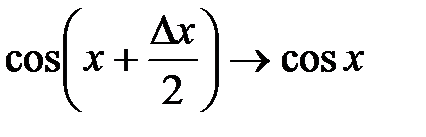 (из-за непрерывности функции
(из-за непрерывности функции  ). Таким образом,
). Таким образом,  .
. производную, называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала
производную, называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала  , называется дифференцируемой на этом интервале.
, называется дифференцируемой на этом интервале.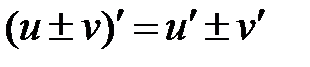 .
.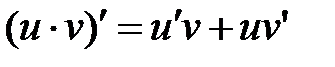 .
. .
.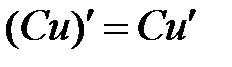 .
. .
.
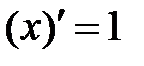 .
.

 .
.


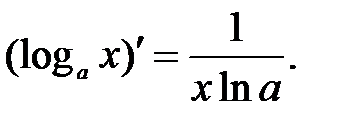
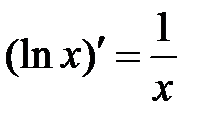 .
.
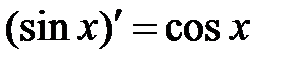 .
.

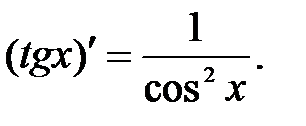
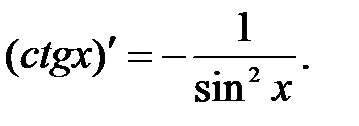
 .
.
 .
.
 .
.
 .
.
 .
. .
. .
.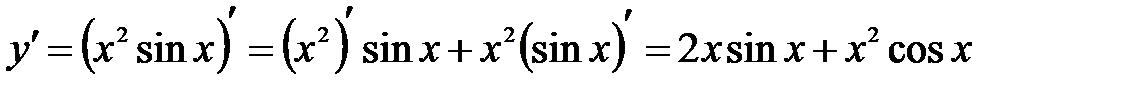 .
. .
.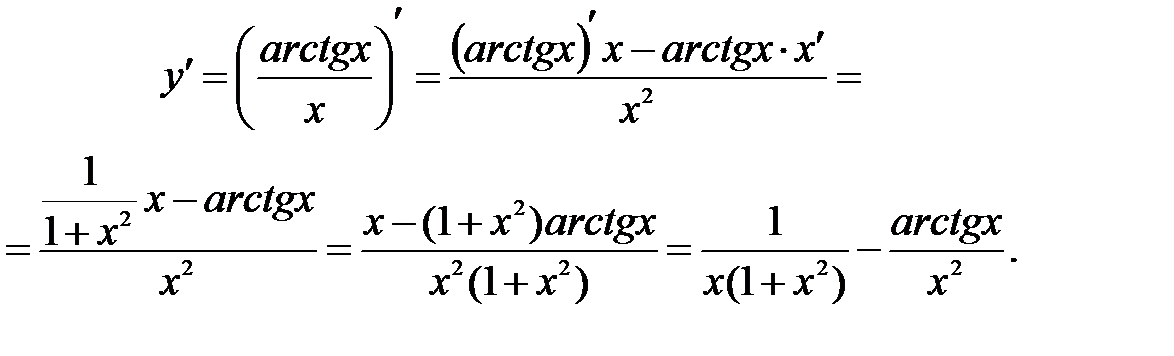
 есть функция от переменной
есть функция от переменной  (
( ), а переменная
), а переменная  в свою очередь есть функция от независимой переменной
в свою очередь есть функция от независимой переменной  (
(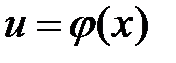 ), т.е. задана сложная функция
), т.е. задана сложная функция 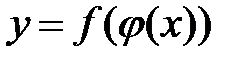 . Функция
. Функция 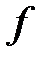 является внешней функцией, а функция
является внешней функцией, а функция  – внутренней.
– внутренней. и
и 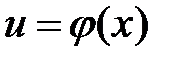 – дифференцируемые функции от своих аргументов, то производная сложной функции
– дифференцируемые функции от своих аргументов, то производная сложной функции  .
. .
.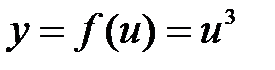 , где
, где 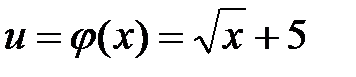 . Тогда, согласно теореме 8.1 о производной сложной функции, будем иметь:
. Тогда, согласно теореме 8.1 о производной сложной функции, будем иметь: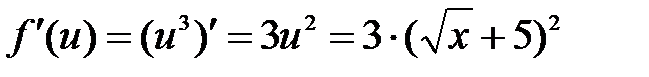 ;
; ;
; .
. .
.


