
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Институт информационных технологий и автоматизацииСтр 1 из 4Следующая ⇒
Институт информационных технологий и автоматизации Кафедра интеллектуальных систем и защиты информации ЗАДАНИЕ На курсовую работу Студенту Института Информационных технологий и автоматизации Курс: 1 Группа: МДА-9 (очная форма обучения) Направление подготовки: 10.03.01 Информационная безопасность Профиль: Безопасность компьютерных систем (в коммерческих структурах) Дисциплина: Математическая логика 1. Тема курсовой работы: Использование методов минимизации булевых функций для построения комбинационных схем 2. Срок сдачи курсовой работы: 3. Исходные данные по курсовой работе: Электронные ресурсы 4. Перечень вопросов, подлежащих разработке в курсовой работе: Найти МДНФ и МКНФ с применением различных методов. Построить комбинационные схемы в булевом базисе и в базисе Жегалкина, реализующие не полностью определенную булеву функцию f(x) = f(X1,X2,X3,X4,X5), которая принимает значение 1 при условии: 2 < |(X2X10)10 - (X3X4X5)10| <= 5 неопределенное значение при условии: |(X2X10)10 - (X3X4X5)10| = 1 (Вариант № 5) 5. Комбинационные схемы имеют следующие наложенные условия: коэффициент объединения по входам - 2, коэффициент разветвления по выходу – 1. 6. Итогом работы являются комбинационные схемы, реализующие заданную функцию и построенные на логических элементах булева базиса и базиса Жегалкина. Дата выдачи задания: 13.02.2020 Задание выдала: ст. преподаватель._____________________ Задание принял к исполнению: Оглавление ЗАДАНИЕ. 2 1. ВВЕДЕНИЕ. 4 2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 5 3. ПРАКТИЧЕСКАЯ ЧАСТЬ. 10 3.1. СОСТАВЛЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ.. 10 3.1.1 ПРЕДСТАВЛЕНИЕ БУЛЕВОЙ ФУНКЦИИ В АНАЛИТИЧЕСКОМ ВИДЕ С ПОМОЩЬЮ КДНФ И ККНФ.. 11 3.2 МИНИМИЗАЦИЯ БУЛЕВОЙ ФУНКЦИИ.. 12 3.2.1 МЕТОД КВАЙНА – МАК-КЛАСКИ.. 12 3.2.2. МЕТОД ПЕТРИКА.. 16 3.2.3. МЕТОД КАРТ КАРНО.. 18 3.2.3.1. ДЛЯ МДНФ.. 18 3.2.3.2. ДЛЯ МКНФ.. 18 3.3 ФАКТОРИЗАЦИЯ И ДЕКОМПОЗИЦИЯ БУЛЕВОЙ ФУНКЦИИ.. 21 3.4 ПОСТРОЕНИЕ КОМБИНАЦИОННЫХ СХЕМ.. 23 3.4.1. КОМБИНАЦИОННАЯ СХЕМА (НЕФАКТОРИЗОВАННОЙ МДНФ) 23 3.4.2. КОМБИНАЦИОННАЯ СХЕМА (КАРТЫ КАРНО) 24 3.4.3. КОМБИНАЦИОННАЯ СХЕМА (ФАКТОРИЗОВАННОЙ МДНФ) 25 3.4.4 КОМБИНАЦИОННАЯ СХЕМА (В БАЗИСЕ ЖЕГАЛКИНА) 26 3.5 УСЛОВНЫЕ ОБОЗНАЧЕНИЯ.. 30 4. ЗАКЛЮЧЕНИЕ. 31 5. СПИСОК ЛИТЕРАТУРЫ.. 33 ВВЕДЕНИЕ Главной целью данной курсовой является знаний в области упрощения булевых функций и применение новых знаний на практике.
Эффективность синтезируемых схем зависит в основном от двух факторов: цены входящих в нее логических элементов и задержки проходящего по ней сигнала по самому длинному пути от входа до выхода. В данной курсовой работе выбран критерий цены. Для этого используется цена схемы по Квайну. Для уменьшения цены нужно решить несколько задач, а именно: минимизации, факторизации и декомпозиции булевых выражений. Чтобы минимизировать логическое выражение можно воспользоваться несколькими способами. Метод Квайна-Мак-Класки (К-М-К), основан на кубическом представлении булевых выражений. Он удобен тем, что выполняется по-простому, но времязатратному, алгоритму, формализован и эффективен. По нему будет найдена минимальная дизъюнктивная нормальная форма. Второй метод - метод карт Карно. Он является более простым и более интуитивным. Данным методом найдем минимальную как конъюнктивную, так и дизъюнктивную формы. Минимальные формы не всегда самые выгодные по цене, поэтому для дальнейшего уменьшения цены будут применены факторизация и декомпозиция. Минус этих способов в том, что они обычно увеличивают задержку. Булева функция от 5ти переменных 2 < |(X2X10)10 - (X3X4X5)10| <= 5 задана в качестве исходной. Данная функция является неопределенной при условии |(X2X10)10 - (X3X4X5)10| = 1. В итоге будут построены комбинационные схемы, реализующие данную функцию, с учетом наименьшей цены.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Булевой функцией называется функция, аргументами которой являются булевы переменные, а сама функция принимает значение из множества {0,1}. Ранг терма - количество букв входящих в терм. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза. Простая дизъюнкция: · полная, если в неё каждая переменная (или её отрицание) входит ровно один раз; · монотонная, если она не содержит отрицаний переменных. Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
Простая конъюнкция: · полная, если в неё каждая переменная (или её отрицание) входит ровно 1 раз; · монотонная, если она не содержит отрицаний переменных. Конъюнктивная нормальная форма, КНФ — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов. Дизъюнктивная нормальная форма, ДНФ — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов. Совершенная (каноническая) конъюнктивная нормальная форма, СКНФ — это такая КНФ, которая удовлетворяет условиям: · в ней нет одинаковых простых дизъюнкций · каждая простая дизъюнкция полная Совершенная (каноническая) дизъюнктивная нормальная форма, СДНФ — ДНФ, удовлетворяющая условиям: · в ней нет одинаковых простых конъюнкций, · каждая простая конъюнкция полная. Конституентой единицы (нуля) называется конъюнктивный (дизъюнктивный) терм максимального ранга, т.е. для булевой функции от n переменных конституента включает в себя n букв. Конституенты единицы (нуля) — элементарные конъюнкции (дизъюнкции), если они содержат в прямом или инверсном виде все переменные, являющиеся аргументами булевой функции. Конституента единицы принимает единичное значение тогда и только тогда, когда все входящие в конституенту буквы принимают значения, равные единице. Конституента нуля принимает нулевое значение тогда и только тогда, когда все входящие в конституенту буквы принимают значение, равное нулю. В кубическом представлении булевой функции от n переменных все множество из 2n наборов ее аргументов рассматривается как множество координат вершин n-мерного куба с длиной ребра равной 1. В соответствии с этим наборы аргументов, на которых булева функция принимает значение равное 1 принято называть существенными вершинами. Существенные вершины образуют так называемые ноль-кубы (0-кубы). Между 0-кубами существует отношение соседства и определена операция склеивания. Два 0-куба называются соседними, если они отличаются только по одной координате. В продолжение аналогии: два r-куба называются соседними, если они отличаются только по одной координате. Покрытием булевой функции f называется такое подмножество кубов из кубического комплекса K(f), которое покрывает все существенные вершины функции. Покрытие булевой функции, которое соответствует минимальной ДНФ, называется минимальным покрытием. ДНФ, соответствующая множеству максимальных кубов, называется сокращенной (СДНФ). Множество максимальных кубов, без которых не может быть образовано покрытие булевой функции, называется ядром покрытия и обозначается T(f) (например, T(f) = {0110-, 11-01}. Цена покрытия используется при решении задачи минимизации булевых функций как количественная оценка качества покрытия с точки зрения его минимальности. Эта оценка базируется на понятии цены кубов, составляющих покрытие. Минимальным покрытием называется покрытие, обладающее минимальной ценой Sa по сравнению с любым другим покрытием этой функции. Булева функция g(X) называется импликантой булевой функции f(X), если для любого набора аргументов, на которых g(X)=1, f(X) также равна единице. Простой (первичной) импликантой булевой функции называется конъюнктивный терм, который сам является импликантой этой функции, но никакая его собственная часть уже не является импликантой этой функции.
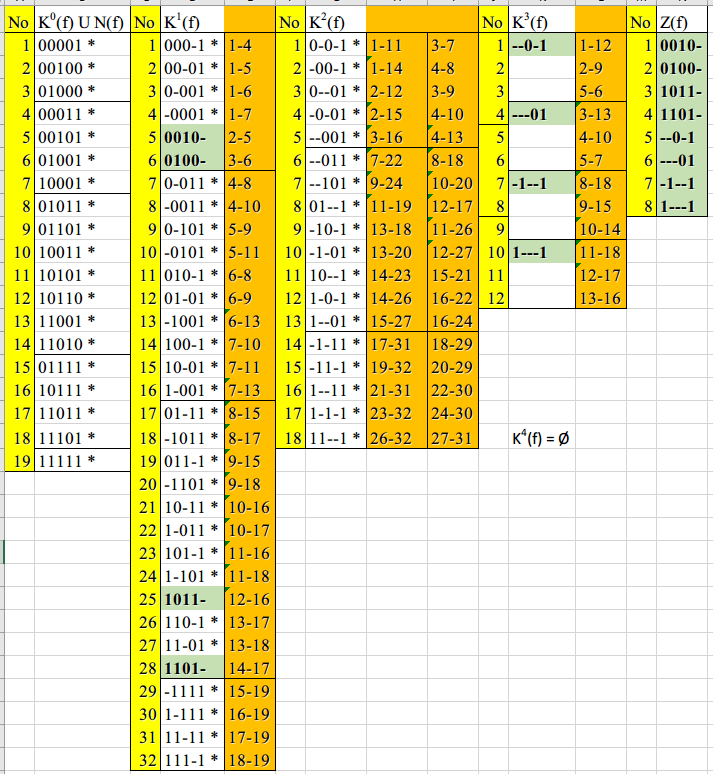
Под собственной частью терма понимается новый терм, полученный из исходного, путем вычеркивания произвольного числа букв. Дизъюнкция всех простых импликант булевой функции представляет собой ДНФ этой функции, которая называется сокращенной - СДНФ. Простая импликанта булевой функции называется существенной, если она и только она покрывает некоторую существенную вершину этой функции. Нахождение минимальных форм булевой функции методом Квайна-Мак-Класки базируется на ее кубическом представлении. При этом куб минимальной размерности (0-куб) отождествляется с набором аргументов булевой функции, на котором он принимает значение, равное единице. Над кубами одинаковой размерности определена операция склеивания, соответствующая правилу склеивания конъюнктивных термов. Склеивание двух k-кубов (размерность k куба определяется числом независимых координат, отмечаемых в записи куба символом -) в результате дает один (k+1)-куб. Проводя всевозможные операции склеивания между кубами можно получить множество кубов различных размерностей, образующих кубический комплекс K(f) заданной функции f(x). С использованием кубического представления булевой функции решение задачи минимизации сводится к получению так называемого минимального покрытия, т.е. покрытия, обладающего минимальной ценой. При этом для получения МДНФ используется единичное покрытие. Таблица Карно (ТК) это видоизмененная запись таблицы истинности. Правила построения ТК следующие: 1) Количество клеток ТК равно количеству строк таблицы истинности. 2) Слева и сверху располагаются значения аргументов. Порядок размещения аргументов таков, что в двух соседних по горизонтали и вертикали клетках отличается значение только одного аргумента (поэтому соседними считаются и клетки, находящиеся на противоположных краях таблицы). 3) В клетки заносятся соответствующие значения логической функции (ЛФ). 4) Единичные клетки объединяются в прямоугольники (импликанты) по 2n клеток. 5) Для каждого прямоугольника записывается конъюнкция тех аргументов, которые в соседних клетках не изменяют своего значения. 6) Переменные входят в конъюнкцию в прямом виде, если их значение в соседних клетках равно 1, в противном случае в обратном.
7) Полученные конъюнкции литералов объединяются через дизъюнкции Метод Петрика основан на составлении булева выражения, определяющего условие покрытия всех существенных вершин булевой функции из упрощенной импликантной таблицы. Булево выражение представляет собой конъюнкцию дизъюнктивных термов, каждый из которых включает в себя совокупность всех простых импликант, покрывающих одну существенную вершину функции. Полученное выражение преобразуется в дизъюнктивную форму и минимизируется с использованием законов поглощения и тавтологии. Каждый конъюнктивный терм дизъюнктивной формы соответствует одному из вариантов покрытия, из которых выбирается минимальное.
ПРАКТИЧЕСКАЯ ЧАСТЬ МИНИМИЗАЦИЯ БУЛЕВОЙ ФУНКЦИИ МЕТОД КВАЙНА – МАК-КЛАСКИ Чтобы получить сокращенную ДНФ булевой функции из ее совершенной ДНФ по теореме Квайна, надо выполнить всевозможные неполные склеивания соседних конъюнкций, а затем всевозможные поглощения конъюнкций. Мак Класки сформулировал алгоритм, который организует построение сокращенной ДНФ более эффективно, чем это предложено в теореме. Для использования метода Квайна-Мак-Класки для начала необходима таблица истинности для 0-куба. Для достижения максимального r-куба d в исходной таблице истинности заменяется на 1.
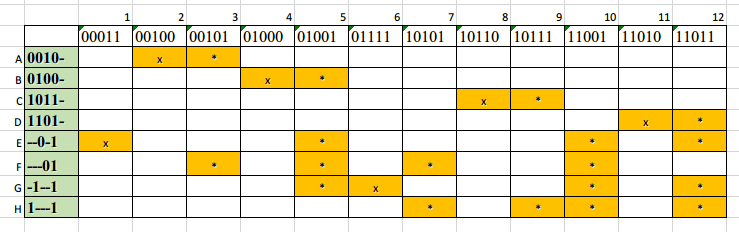
Таблица 2 Простые импликанты Используя таблицу простых импликантов и проводя операцию склейки, находятся кубы максимальной размерности. Термы, которые не участвовали в операции склейки, отмечены зеленым (простые импликанты) и составляют покрытие Z(f) (Таблица 2). Оно задает СДНФ исходной функции. Склеиваемые термы отмечены *, справа от полученного терма написаны номера, из которых они получились.
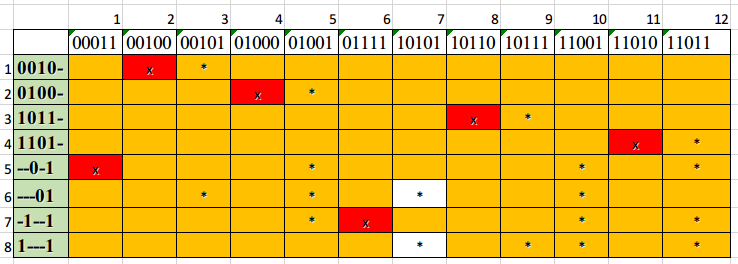
Таблица 3 Импликантная таблица Чтобы отобразить покрытие простыми импликантами существенных вершин составляется имплекантная таблица. Каждая строка это простая импликанта, а каждый столбец – один из 0-кубов (Таблица 3). Для неполностью определенной функции безразличные наборы исключаются. Далее выделяем множество существенных импликант. Находятся столбцы с одной меткой (выделены красным х). Строки соответствующих импликант удаляются (закрашиваются оранжевым), захватавая другие отмеченные * столбцы, которые встречаются в удаляемой строке. Множество всех существенных импликант (строки с красным х, 1-5, 7) образует ядро покрытия Т. T = {0010-; 0100-; 1011-; 1101-; --0-1; -1--1} Термы ядра: Удалив ядро из таблицы получим упрощенную импликантную таблицу (Таблица 4).
Таблица 4 Упрощенная импликантная таблица Термы упрощенной таблицы (выбираем любой, оба покрывают g 0-куб) и добавляем его к ядру покрытия, чтобы получить минимальное покрытие: Сmin = {0010-; 0100-; 1011-; 1101-; --0-1; -1--1; 1---1} 1---1 соответствует X1X5, следовательно МДНФ: f = Вычислим цену покрытия Sa, которая является количеством переменных, участвующих в записи МДНФ; цену покрытия Sb, которая является суммой цены Sa и количества термов МДНФ. Данные цены образуют предельные границы цены схемы по Квайну: Sa ≤ SQ ≤ Sb.
Посчитаем цену покрытия: Sa = 22, Sb = 29 Неравенство ограничения цены схемы по Квайну: 22 ≤ SQ ≤ 29.
МЕТОД ПЕТРИКА Невозможно применить к упрощенной таблице из-за ее маленького объема, поэтому применяем к обычной таблице.
Таблица 5 Таблица для метода Петрика Для метода Петрика нужно выписать булево выражение Y, покрывающее все существенные вершины: Y = EA(A ˅ F)B(B ˅ E ˅ F ˅ G)G(F ˅ H)C(C ˅ H) (E ˅ F ˅ G ˅ H)D(D ˅ E ˅ G ˅ H) Попарно умножив термы с одинаковыми буквами, применив закон поглощения, упростим выражение и приведем его к дизъюнктивной форме: Y = ABCDEG(F v H) = ABCDEGF v ABCDEGH Оба терма состоят из 7ми букв, так что можно выбрать любой. ABCDEGH соответствует минимальному покрытию: Сmin = {0010-; 0100-; 1011-; 1101-; --0-1; -1--1; 1---1} МДНФ ( также не изменилась): f = Цена не изменилась: Sa = 22, Sb = 29 Цена по методу Квайна – Мак – Класки не изменилась в методе Петрика, потому что в итоге выбирается одинаковое количество импликант с одинаковым покрытием вершин. Метод Квайна – Мак – Класки скорее визуальный, а метод Петрика позволяет точно вычислить каждую комбинацию импликантов и покрытых вершин, где потом выбирается вариант с минимальным покрытием.
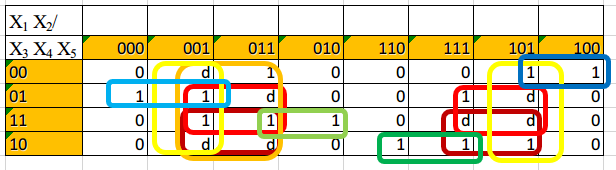
МЕТОД КАРТ КАРНО ДЛЯ МДНФ Для определения МДНФ функции рассмотрим карты с единичными значениями функции, а также доопределим значение d до единицы (Таблица 6). Выделяем области с максимальным количеством единиц, которые могут содержать количество элементов кратное двум в степени n, те. 2, 4, 8..
Таблица 6 Карты Карно при МДНФ
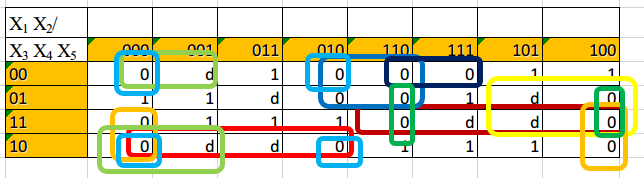
ДЛЯ МКНФ Для определения МКНФ функции рассмотрим карты с нулевыми значениями функции, а также доопределим значение d до нуля (Таблица 7). Выделяем области с максимальным количеством нулей, которые могут содержать количество элементов кратное двум в степени n, те. 2, 4, 8..
Таблица 7 Карты Карно при МКНФ
Посчитаем цену покрытия: Sa = 28, Sb = 37 Неравенство ограничения цены схемы по Квайну: 28 ≤ SQ ≤ 37.
Сравним цены различных МДНФ и МКНФ. Границы для МДНФ: Ограничения цены схемы по Квайну, метод К-М-К: 22 ≤ SQ ≤ 29. Ограничения цены схемы по Квайну, метод Петрика: 22 ≤ SQ ≤ 29 Ограничения цены схемы по Квайну, метод карт Карно: 24 ≤ SQ ≤ 32 Границы для МКНФ: Ограничения цены схемы по Квайну, метод карт Карно: 28 ≤ SQ ≤ 37 Для факторизации и декомпозиции берем МДНФ, полученную методом К-М-К и методом карт Карно, потому что они имеют наименьшую Sa, равную 22 и 24.
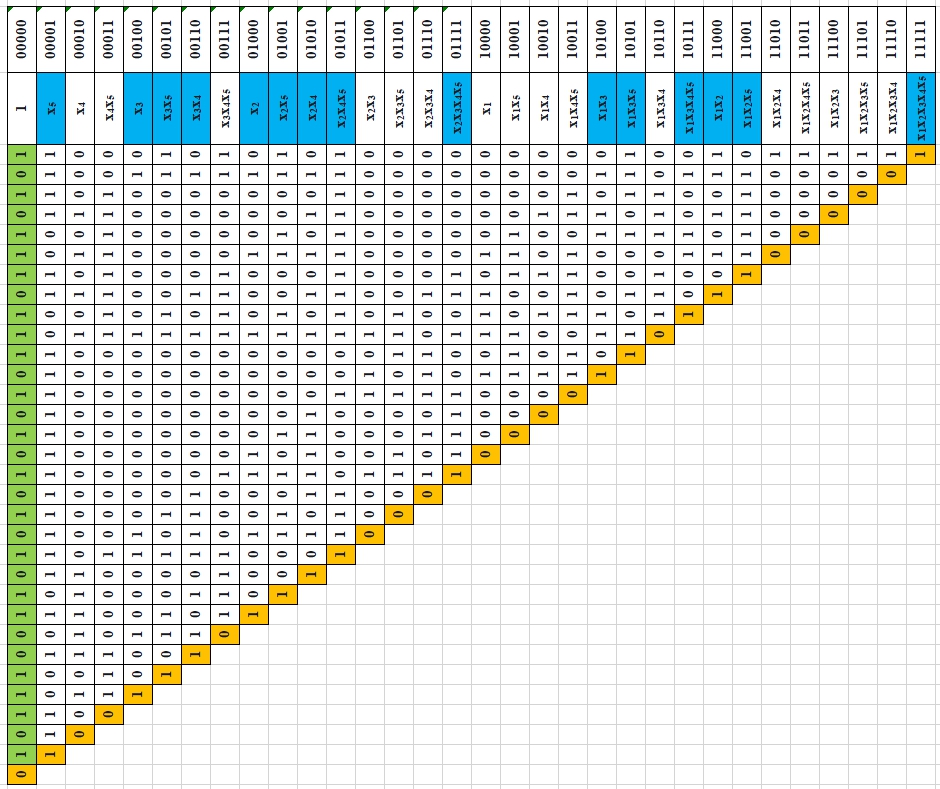
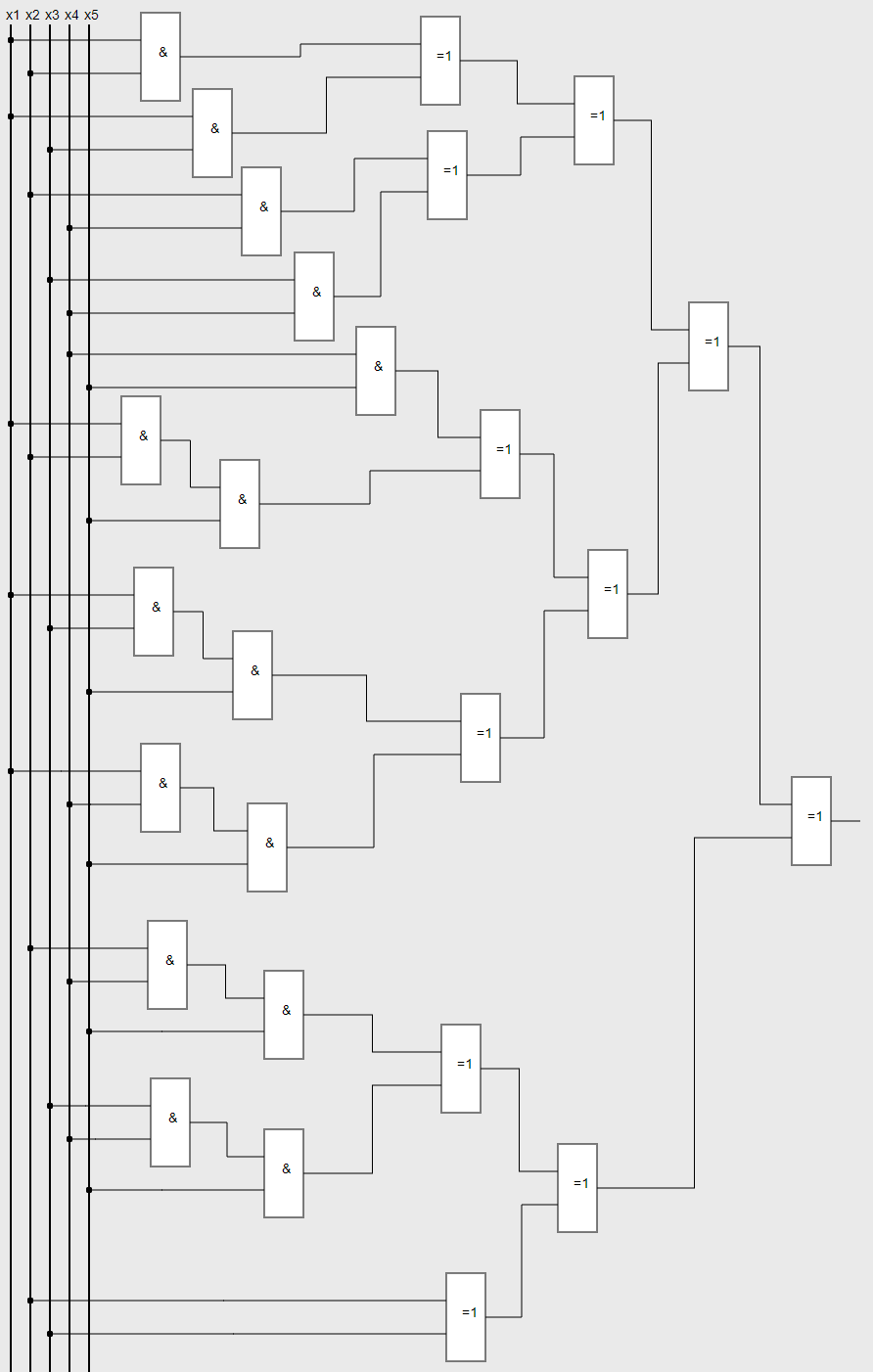
КОМБИНАЦИОННАЯ СХЕМА (В БАЗИСЕ ЖЕГАЛКИНА) Для начала преобразуем КДНФ с помощью треугольника Паскаля в базис Жегалкина. Составим два треугольника, один с d равным 0 (Рисунок 4), второй с d равным 1 ( Рисунок 5).
Рисунок 4 Треугольник Паскаля, d = 0 f = x2 ⊕ x3 ⊕ x1x2 ⊕ x1x3 ⊕ x2x4 ⊕ x3x4 ⊕ x4x5 ⊕ x1x2x5 ⊕ x1x3x5 ⊕ x1x4x5 ⊕ x2x4x5 ⊕ x3x4x5 SQ = 27 + 12 = 39
Рисунок 5 Треугольник Паскаля, d = 1 f = x2 ⊕ x3 ⊕ x5 ⊕ x1x2 ⊕ x1x3 ⊕ x2x4 ⊕ x2x5 ⊕ x3x4 ⊕ x3x5 ⊕ x1x2x5 ⊕ x1x3x5 ⊕ x2x4x5 ⊕ x1x3x4x5 ⊕ x2x3x4x5 ⊕ x1x2x3x4x5 SQ = 37 + 15 = 52 Первый полином Жегалкина имеет меньшую цену из двух, поэтому его мы отобразим на комбинационной схеме (Рисунок 6).
X5⊕X3⊕X3X5⊕X3X4⊕X2⊕X2X5⊕X2X4⊕X2X4X5⊕X2X3X4X5⊕X1X3⊕X1X3X5⊕X1X3X4X5⊕X1X2⊕X1X2X5⊕X1X2X3X4X5
Рисунок 6 Комбинационная схема в базисе Жегалкина Задержка: Т = 6τ. Цена схемы по Квайну: SQ = 52 (цена больше, чем по формуле из-за ограничений на входы) УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Знак дизъюнкции – v; Знак конъюнкции опускается; Знак отрицания – надчеркивание ( Знак сложения по модулю 2 – ⊕; При склейке 1 и 0 превращаются в - Пересечения вершин и импликант отмечены знаком *, элементы ядра - х; Вычеркнутые строки и столбцы выделены оранжевым цветом.
ЗАКЛЮЧЕНИЕ В данной работе булево выражение 2 < |(X2X10)10 - (X3X4X5)10| <= 5 с неопределенными термами заданными функцией |(X2X10)10 - (X3X4X5)10| = 1 было рассмотрено в двух базисах: логическом (3 операции) и Жегалкина (2 операции). При интегральной технологии с точки зрения надежности и стоимости использование однотипных элементов весьма предпочтительно. На мой взгляд было бы интересно изучить функцию в других базисах, например «И-НЕ» (функция Шеффера) и «ИЛИ-HE» (функция Пирса), чтобы сравнить насколько они эффективней полинома Жегалкина. В перспективе было бы интересно поменять основной критерий эффективности с цены по Квайну на задержку сигнала. Данная курсовая работа может представлять интерес для людей тесно связанных с комбинационными схемами и их проектированием. В процессе написания курсовой работы я научился минимизации булевых функций с помощью метода К-М-К, метода Петрика и карт Карно. Определив наиболее минимальную форму, были построены четыре схемы: МДНФ по методу К-М-К, она же после факторизации, факторизованная МДНФ полученная по методу карт Карно, а также МДНФ в базисе Жегалкина. Наиболее трудоемким оказался метод К-М-К, потому что он требует длительной концентрации внимания при склеивании кубов. В данной работе было произведено 32+18*2+12 = 80 склеек. От результата этого метода зависят две комбинационные схемы и факторизация с декомпозицией, поэтому ошибка на начальных этапах может дорого стоить. Результаты курсовой работы заставили меня обратить внимание на следующие пункты: - факторизация может улучшить цену, не меняя задержку. В моем случае так и вышло. Задержка не изменилась, цена снизилась. - декомпозиция не всегда возможна для улучшения характеристик схемы. Я не нашел способа эффективной замены на новую функцию. - сложность минимизации различна при использовании разных методов. Метод К-М-К прост по своей сути, но требует хорошей концентрации, чтобы не допустить ошибок. Метод карт Карно требует развитое воображение, чтобы увидеть какие зоны самые большие и как их можно объединить. - цена минимальной функции была различна для разных методов, самая низкая была найдена при использовании метода К-М-К и дальнейшей факторизации. Благодаря нескольким итерациям исправления ошибок, используемые методы прочно закрепились в моей памяти. СПИСОК ЛИТЕРАТУРЫ 1. Рябова О. Н. Математическая логика. Курсовая работа: методические указания к выполнению курсовой работы для студентов направления бакалавриата / О. Н. Рябова – СПб: СПбГУПТД 2019. – 34 с. 2. Тѐрушкина, О. Б. Математическая логика. Курсовая работа: методические указания к выполнению курсовой работы для студентов подготовки бакалавриата / О. Б. Тѐрушкина – СПб: СПбГУПТД, 2017. – 15 с. 3. Редактор схемы логических элементов Режим доступа: https://www.semestr.online/graph/logic-gate.php. (Дата: 19.06.2020) 4. Онлайн-калькулятор для метода Петрика Режим доступа: https://www.kontrolnaya-rabota.ru/s/mathlogic/. (Дата: 19.06.2020) 5. Довгий П. С. Синтез комбинационных схем: учебно-метод.пособие к курсовой работе по дисциплине «Дискретная математика» / П. С. Довгий, В. И. Поляков. – СПб: СПбГУ ИТМО, 2009. – 64 с. 6. Новиков Ф.А. Дискретная математика для программистов: учебник для вузов. 2-е изд.- Питер, 2006.- 368 с. 7. ГОСТ 7.32-2001, ГОСТ 7.0.3-2006, ГОСТ 7.1-2003 Институт информационных технологий и автоматизации
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.202 (0.134 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
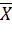 1
1 

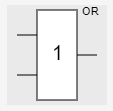 логический элемент (лэ) или
логический элемент (лэ) или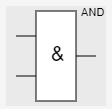 лэ и
лэ и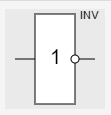 лэ инвертор
лэ инвертор лэ модуль 2
лэ модуль 2


