Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения Максвелла в гиперболической форме PDE
Уравнения Максвелла можно сформулировать как гиперболическую систему уравнений в частных производных. Это дает доступ к мощным методам численных решений. Предполагается,что волны распространяются в плоскости (x, y) и ограничивают направление магнитного поля, параллельного оси z, и, следовательно, электрическое поле, параллельное плоскости (x, y). Эта волна называется поперечной магнитной (ТМ) волной. В 2D и без поляризационных терминов уравнения Максвелла могут быть сформулированы следующим образом:
где u, A, B и C определяются как
В этом представлении
-также может быть явно определен равным нулю для упрощения определенных задач или для поиска характерного решения, что часто является первым шагом в методе поиска конкретного неоднородного решения. Решатели интегральных уравнений. Дискретное дипольное приближение Дискретная дипольная аппроксимация-это гибкий метод вычисления рассеяния и поглощения мишенями произвольной геометрии. Формулировка основана на интегральной форме уравнений Максвелла. DDA представляет собой аппроксимацию континуальной цели конечным массивом поляризуемых точек. Точки приобретают дипольные моменты в ответ на локальное электрическое поле. Диполи, конечно, взаимодействуют друг с другом через свои электрические поля, поэтому DDA также иногда называют связанным дипольным приближением. Полученная линейная система уравнений обычно решается с использованием сопряженных градиентных итераций. Матрица дискретизации имеет симметрии (интегральная форма уравнений Максвелла имеет форму свертки), что позволяет быстрому преобразованию Фурье умножать матрицу на вектор во время итераций сопряженного градиента.
Метод элементов моментов Метод моментов (MoM) или метод граничных элементов (BEM) - это численный вычислительный метод решения линейных дифференциальных уравнений в частных производных, которые были сформулированы как интегральные уравнения (т. Е. в форме граничного интеграла). Он может быть применен во многих областях техники и науки, включая механику жидкости, акустику, электромагнетизм, механику разрушения и пластичность.
БЕМ стал более популярным с 1980-х годов. Поскольку он требует вычисления только граничных значений, а не значений по всему пространству, он значительно более эффективен с точки зрения вычислительных ресурсов для задач с небольшим соотношением поверхности и объема. Концептуально он работает, создавая "сетку" над моделируемой поверхностью. Однако для многих задач БЭМ значительно менее эффективны в вычислительном отношении, чем методы дискретизации объема (метод конечных элементов, метод конечных разностей, метод конечных объемов). Формулировки граничных элементов обычно приводят к появлению полностью заполненных матриц. Это означает, что требования к хранилищу и вычислительное время будут расти в соответствии с квадратом размера проблемы. Напротив, матрицы конечных элементов, как правило, связаны (элементы связаны только локально), и требования к хранению для системных матриц, как правило, линейно растут с размером задачи. Методы сжатия (например, мультипольные разложения или адаптивная перекрестная аппроксимация/иерархические матрицы) могут быть использованы для улучшения этих задач, хотя и за счет дополнительной сложности и с коэффициентом успеха, который в значительной степени зависит от характера и геометрии задачи. БЭМ применим к задачам, для которых могут быть вычислены функции Грина. Они обычно включают поля в линейных однородных средах. Это накладывает значительные ограничения на диапазон и общность задач, подходящих для граничных элементов. Нелинейности могут быть включены в формулировку, хотя они обычно вводят интегралы объема, которые требуют дискретизации объема перед решением, устраняя часто упоминаемое преимущество BEM.
Сравнение результатов моделирования и аналитической формулировки Например, оценка значения радиолокационного сечения пластины с помощью аналитической формулы:
где A - поверхность пластины, -длина волны. Следующая кривая, представляющая RCS пластины, вычисленной на частоте 35 ГГц, может быть использована в качестве эталонного примера. Когда сложность теоретических формул делает аналитическое решение трудноразрешимым, мы прибегаем к неаналитическим методам, которые включают графические методы, экспериментальные методы, аналоговые методы и численные методы. Графические, экспериментальные и аналоговые методы применимы для решения относительно небольшого числа задач. Численные методы получили известность и стали более привлекательными с появлением быстрых цифровых компьютеров. Наиболее часто используемыми простыми численными методами в ЭМ являются метод моментов, метод конечных разностей, метод конечных элементов и метод моделирования заряда. Большинство задач ЭМ связаны либо с уравнениями в частных производных, либо с интегральными уравнениями. Дифференциальные уравнения в частных производных обычно решаются методом конечных разностей или методом конечных элементов; интегральные уравнения удобно решать методом моментов. Хотя численные методы дают приближенные решения, эти решения достаточно точны для инженерных целей. У нас не должно сложиться впечатление, что аналитические методы устарели из-за численных методов; скорее, они дополняют друг друга. Каждый численный метод включает в себя аналитическое упрощение до такой степени, что его легко применить.
Графические методы Эти методы анализируют данную проблему, используя различные таблицы и диаграммы, такие как диаграммы линий передачи, диаграммы Смита и т. д. Вариации проблемы отображаются на этих диаграммах, и соответствующие наблюдения отмечаются. Их использование ограничено уравнениями Лапласа для двумерных геометрий, поскольку они, как правило, основаны на свойствах аналитических функций. Существуют некоторые ограничения в графических методах. Их точность ограничена даже при тщательном применении. Методы моментов Метод моментов-это мощный вычислительный метод, который является частично аналитическим и частично вычислительным. Этот метод очень эффективен для анализа геометрии открытых областей, таких как антенны, рассеиватели и плоские схемы. Метод основан на методе взвешенных остатков, в котором остаток управляющего уравнения устанавливается равным нулю в среднем по области. Неизвестная функция расширяется в наборе функций расширения, а внутреннее произведение остатка устанавливается равным нулю. Число тестовых функций принимается равным числу функции разложения, чтобы генерировать столько уравнений, сколько есть неизвестных. MoM иллюстрируется решением ряда примеров, таких как емкость полосовой линии, распределение заряда на металлической проволоке, распределение тока и входное сопротивление полуволнового диполя и RCS цилиндрического рассеивателя. MOM-это метод, используемый для решения электромагнитных граничных или объемных интегральных уравнений в частотной области. Поскольку электромагнитные источники представляют интерес, MOM очень полезен в решении проблемы излучения и рассеяния. Новый метод интеграции, основанный на использовании квази. Предложена методика интегрирования по методу Монте-Карло (QMCI) для метода решения моментов
интегрального уравнения для расчета емкости. Сформулировано интегральное уравнение для неизвестного распределения заряда по конденсаторам. Решения получены методом MOM с использованием метода QMCI. Он обеспечивает точное вычисление емкостей параллельных пластинчатых, цилиндрических и сферических конденсаторов.
5.7 Метод конечных элементов Метод конечных элементов берет свое начало в области структурного анализа. Этот метод не применялся к задачам ЭМ до 1968 года. Как и метод конечных разностей, метод конечных элементов полезен при решении дифференциальных уравнений. Метод конечных разностей представляет область решения с помощью массива точек сетки; его применение становится затруднительным из-за проблем, имеющих границы неправильной формы. Такие проблемы могут быть решены более легко с помощью метода конечных элементов. Анализ конечных элементов любой задачи включает в себя в основном четыре шага: (а) дискретизация области решения на конечное число элементов, (б) вывод управляющих уравнений для типичного элемента, (в) сборка всех элементов в области решения и (г) решение полученной системы уравнений. Метод моделирования заряда Метод моделирования заряда очень полезен для решения уравнений в частных производных в электротехнике и был изучен и разработан многими исследователями. Этот метод прост для понимания и может быть применен только путем решения системы одновременных линейных уравнений. Многие примеры показывают, что метод позволяет получить достаточно точные решения краевых задач относительно областей, ограниченных гладкими кривыми.
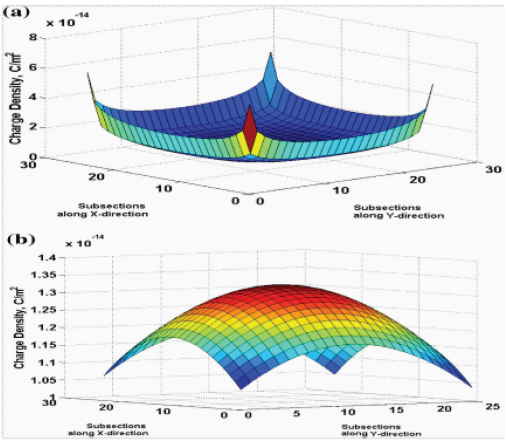
5.8 Общий анализ В области расчета емкости уже проделана значительная работа. Проанализирована оценка емкости на единицу длины металлического прямоугольного параллелепипеда с диэлектрическим покрытием для геометрии (Prarthana D. Mehta & S. B. Chakrabarty,). Распределение заряда по поверхности металлической грани прямоугольного параллелепипеда и соответствующей грани диэлектрического покрытия для верхней грани представлено на рис. 1(а)и (б) соответственно. Валидность анализа была обоснована сравнением данных по емкость, имеющаяся в литературе для металлического куба и полого цилиндра с верхней и нижней накладками, с данными о емкости, вычисленными настоящим методом для аналогичных структур с учетом очень низкой диэлектрической проницаемости, а также очень тонкого диэлектрического покрытия. Проанализирована оценка емкости единичного куба с помощью программы MATLAB. Для определения распределения заряда и емкости проводящих структур была разработана компьютерная программа, основанная на предыдущих формулировках. Выбор этой программы основан на ее широкой доступности в университетах и отраслях промышленности и простоте использования. Чтобы использовать метод подобластей, авторы делят общую площадь поверхности a2 одной стороны куба на несколько подобластей.
Рис.5.1 Распределение заряда по направлению X-Y (а) верхняя проводящая грань (б) Диэлектрическое покрытие верхней проводящей грани
|
|||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.102.112 (0.01 с.) |
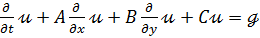 (5.1)
(5.1)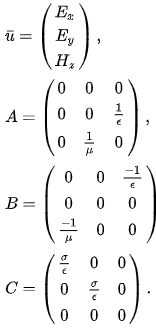 (5.2)
(5.2)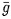 является принудительной функцией и находится в том же пространстве, что и u. Он может быть использован для выражения внешнего прикладного поля или для описания ограничения оптимизации. Как сформулировано выше:
является принудительной функцией и находится в том же пространстве, что и u. Он может быть использован для выражения внешнего прикладного поля или для описания ограничения оптимизации. Как сформулировано выше: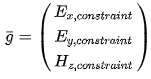 (5.3)
(5.3) , (5.4)
, (5.4)