Простейшие тригонометрические уравнения

Простейшие тригонометрические уравнения

Простейшими называются уравнения sinx=a,cosx=a,tgx=a,ctgx=asinx=a,cosx=a,tgx=a,ctgx=a, где xx — угол, который нужно найти, aa — любое число. Запишем для каждого из них формулы корней.

1. Уравнение sinx=asinx=a.

При |a|>1|a|>1 не имеет решений.

При |a|≤1|a|≤1 имеет бесконечное число решений.

Формула корней: x=(−1)narcsina+πn,n∈Zx=(-1)narcsina+πn,n∈Z

Таблица арксинусов

2. Уравнение cosx=acosx=a

При |a|>1|a|>1 — как и в случае с синусом, решений среди действительных чисел не имеет.

При |a|≤1|a|≤1 имеет бесконечное множество решений.

Формула корней: x=±arccosa+2πn,n∈Zx=±arccosa+2πn,n∈Z

Таблица арккосинусов

Частные случаи для синуса и косинуса в графиках.

3. Уравнение tgx=atgx=a

Имеет бесконечное множество решений при любых значениях aa.

Формула корней: x=arctga+πn,n∈Zx=arctga+πn,n∈Z

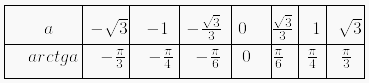
Таблица арктангенсов

4. Уравнение ctgx=actgx=a

Также имеет бесконечное множество решений при любых значениях aa.

Формула корней: x=artga+πn,n∈Zx=artga+πn,n∈Z

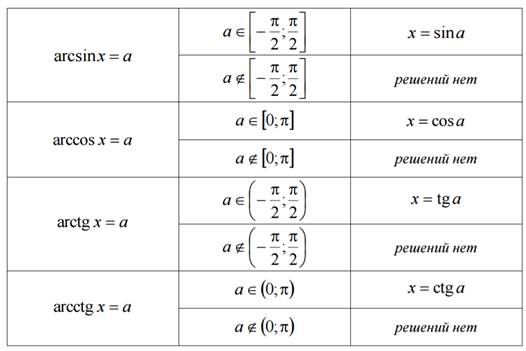
Таблица арккотангенсов

Формулы корней тригонометрических уравнений в таблице

Для синуса:

Для косинуса:

Для тангенса и котангенса:

Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений

Решение любого тригонометрического уравнения состоит из двух этапов:

• с помощью тригонометрических формул преобразовать его до простейшего;
• решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.

Рассмотрим на примерах основные методы решения.

Алгебраический метод.

В этом методе делается замена переменной и ее подстановка в равенство.

Пример. Решить уравнение: 2cos2(x+π6)−3sin(π3—x)+1=02cos2(x+π6)-3sin(π3—x)+1=0

Решение. Используя формулы приведения, имеем:

2cos2(x+π6)−3cos(x+π6)+1=02cos2(x+π6)-3cos(x+π6)+1=0,

делаем замену: cos(x+π6)=ycos(x+π6)=y, тогда 2y2−3y+1=02y2-3y+1=0,

находим корни: y1=1,y2=12y1=1,y2=12, откуда следуют два случая:

1. cos(x+π6)=1cos(x+π6)=1, x+π6=2πnx+π6=2πn, x1=−π6+2πnx1=-π6+2πn.

2. cos(x+π6)=12cos(x+π6)=12, x+π6=±arccos12+2πnx+π6=±arccos12+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn.

Ответ: x1=−π6+2πnx1=-π6+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn.

Разложение на множители.

Пример. Решить уравнение: sinx+cosx=1sinx+cosx=1.

Решение. Перенесем влево все члены равенства: sinx+cosx−1=0sinx+cosx-1=0. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:

sinx—2sin2 x2=0sinx—2sin2 x2=0,

2sin x2cos x2−2sin2 x2=02sin x2cos x2-2sin2 x2=0,

2sin x2(cos x2−sin x2)=02sin x2(cos x2-sin x2)=0,

1. sin x2=0sin x2=0, x2=πnx2=πn, x1=2πnx1=2πn.
2. cos x2−sin x2=0cos x2-sin x2=0, tg x2=1tg x2=1, x2=arctg1+πnx2=arctg1+πn, x2=π4+πnx2=π4+πn, x2=π2+2πnx2=π2+2πn.

Ответ: x1=2πnx1=2πn, x2=π2+2πnx2=π2+2πn.

Переход к половинному углу

Пример. Решить уравнение: 11sinx—2cosx=1011sinx—2cosx=10.

Решение. Применим формулы двойного угла, в результате: 22sin(x2)cos(x2)−22sin(x2)cos(x2)- 2cos2x2+2sin2x2=2cos2x2+2sin2x2= 10sin2x2+10cos2x210sin2x2+10cos2x2

4tg2x2—11tgx2+6=04tg2x2—11tgx2+6=0

Применив описанный выше алгебраический метод, получим:

1. tgx2=2tgx2=2, x1=2arctg2+2πnx1=2arctg2+2πn, n∈Zn∈Z,
2. tgx2=34tgx2=34, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z.

Ответ. x1=2arctg2+2πn,n∈Zx1=2arctg2+2πn,n∈Z, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z.

Алгебраический метод.

В этом методе делается замена переменной и ее подстановка в равенство.

Пример. Решить уравнение: 2cos2(x+π6)−3sin(π3—x)+1=02cos2(x+π6)-3sin(π3—x)+1=0

Решение. Используя формулы приведения, имеем:

2cos2(x+π6)−3cos(x+π6)+1=02cos2(x+π6)-3cos(x+π6)+1=0,

делаем замену: cos(x+π6)=ycos(x+π6)=y, тогда 2y2−3y+1=02y2-3y+1=0,

находим корни: y1=1,y2=12y1=1,y2=12, откуда следуют два случая:

1. cos(x+π6)=1cos(x+π6)=1, x+π6=2πnx+π6=2πn, x1=−π6+2πnx1=-π6+2πn.

2. cos(x+π6)=12cos(x+π6)=12, x+π6=±arccos12+2πnx+π6=±arccos12+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn.

Ответ: x1=−π6+2πnx1=-π6+2πn, x2=±π3−π6+2πnx2=±π3-π6+2πn.

Разложение на множители.

Пример. Решить уравнение: sinx+cosx=1sinx+cosx=1.

Решение. Перенесем влево все члены равенства: sinx+cosx−1=0sinx+cosx-1=0. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:

sinx—2sin2 x2=0sinx—2sin2 x2=0,

2sin x2cos x2−2sin2 x2=02sin x2cos x2-2sin2 x2=0,

2sin x2(cos x2−sin x2)=02sin x2(cos x2-sin x2)=0,

1. sin x2=0sin x2=0, x2=πnx2=πn, x1=2πnx1=2πn.

2. cos x2−sin x2=0cos x2-sin x2=0, tg x2=1tg x2=1, x2=arctg1+πnx2=arctg1+πn, x2=π4+πnx2=π4+πn, x2=π2+2πnx2=π2+2πn.

Ответ: x1=2πnx1=2πn, x2=π2+2πnx2=π2+2πn.

Переход к половинному углу

Пример. Решить уравнение: 11sinx—2cosx=1011sinx—2cosx=10.

Решение. Применим формулы двойного угла, в результате: 22sin(x2)cos(x2)−22sin(x2)cos(x2)- 2cos2x2+2sin2x2=2cos2x2+2sin2x2= 10sin2x2+10cos2x210sin2x2+10cos2x2

4tg2x2—11tgx2+6=04tg2x2—11tgx2+6=0

Применив описанный выше алгебраический метод, получим:

1. tgx2=2tgx2=2, x1=2arctg2+2πnx1=2arctg2+2πn, n∈Zn∈Z,

2. tgx2=34tgx2=34, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z.

Ответ. x1=2arctg2+2πn,n∈Zx1=2arctg2+2πn,n∈Z, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z.

Простейшие тригонометрические уравнения

Простейшими называются уравнения sinx=a,cosx=a,tgx=a,ctgx=asinx=a,cosx=a,tgx=a,ctgx=a, где xx — угол, который нужно найти, aa — любое число. Запишем для каждого из них формулы корней.

1. Уравнение sinx=asinx=a.

При |a|>1|a|>1 не имеет решений.

При |a|≤1|a|≤1 имеет бесконечное число решений.

Формула корней: x=(−1)narcsina+πn,n∈Zx=(-1)narcsina+πn,n∈Z

Таблица арксинусов

2. Уравнение cosx=acosx=a

При |a|>1|a|>1 — как и в случае с синусом, решений среди действительных чисел не имеет.

При |a|≤1|a|≤1 имеет бесконечное множество решений.

Формула корней: x=±arccosa+2πn,n∈Zx=±arccosa+2πn,n∈Z

Таблица арккосинусов

Частные случаи для синуса и косинуса в графиках.

3. Уравнение tgx=atgx=a

Имеет бесконечное множество решений при любых значениях aa.

Формула корней: x=arctga+πn,n∈Zx=arctga+πn,n∈Z

Таблица арктангенсов

4. Уравнение ctgx=actgx=a

Также имеет бесконечное множество решений при любых значениях aa.

Формула корней: x=artga+πn,n∈Zx=artga+πn,n∈Z

Таблица арккотангенсов