Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебра высказываний. Формулы алгебры высказываний.Стр 1 из 9Следующая ⇒
Алгебра высказываний. Формулы алгебры высказываний. Высказывание - это повествовательное предложение, о котором можно судить истинно оно или ложно. Безличные предложения и вопросительные не являются высказываниями. Пример: Снег чёрный – высказывание. Два умножить на два, равно пять – высказывание. 3<9 высказывание. Добро пожаловать! – не высказывание. Высказывания обозначаются заглавными буквами латинского алфавита A,B,C,R,….,S. A: “3>2” Если высказывание истинно, то значение истинности |A|=1. Если высказывание ложно, то |B|=0. Операции над высказываниями Отрицанием высказывания P называется такое высказывание, обозначаемое ⌐P (не P), которое ложно, если P- истинно, и ложно в противном случае. Конъюнкцией высказываний P и Q называется такое высказывание, обозначаемое P^Q, которое истинно, тогда и только тогда, когда P и Q истинно одновременно. Дизъюнкцией высказываний P и Q называется такое высказывание, обозначаемое PÚQ, которое ложно, тогда и только тогда, когда P и Q ложно одновременно. Импликацией высказываний P и Q называется такое высказывание, обозначаемое P–›Q, которое ложно, тогда и только тогда, когда P истинно, а Q ложно. Эквиваленцией высказываний P и Q называется такое высказывание, обозначаемое P‹–›Q, которое истинно, тогда и только тогда, когда P и Q принимают одинаковые значения истинности. Формулы алгебры высказывания Переменные, вместо которых можно подставлять высказывания, называются пропозиционными переменными. Формулы алгебры высказываний. 1. Каждая пропозиционная переменная, есть формула алгебры высказываний. 2. Если P и Q – это формулы алгебры высказываний, то выражения ⌐P, (P^Q), (PÚQ), (P–›Q), (P‹–›Q) являются формулами алгебры высказываний. 3. Никаких других формул кроме перечисленных в пунктах 1 и 2 нет. Пример: (xÙy)Ú (xy) не формула алгебры высказываний. Все возможные логические значения формулы, в зависимости от значений входящих в неё элементарных высказываний, могут быть описаны полностью с помощью таблицы истинности. Например, для формулы
Свойства тавтологий 1. Формула А является тавтологией тогда и только тогда, когда её отрицание является противоречием. 2. Если формула А является тавтологией, А–›В тавтология, то В тавтология. 3. Если формула А(x1,……xn) – тождественно истинная и формулы В1(y1,….yk), B2(y1,….yk),…,Bn(y1,….yk) – тождественно истинные, то формула А*(y1,….yk) полученная из А, подстановкой в неё формул В1, В2 ,…, Bn является тождественно истинной. Логическое следствие Формула алгебры высказываний В называется логическим следствием совокупности формул А1, А2,…, An, если она принимает значение истина на любом наборе на котором все формулы данной совокупности одновременно истинны. Пример: P–›Q - логическое следствие P‹–›Q, обратное логическое следование не выполняется. Тавтология является следствием любой совокупности формул. Следствием тождественно ложной формулы является любая формула. Равносильность формул Формулы А и В называются равносильными, если на любом наборе значений переменных они принимают одинаковые истинностные значения. АºВ. Пример: X–›Yº⌐XÚ Y Доказательство:
Теорема. Если логическим следствием совокупности формул А1,А2,….Ak,⌐B- противоречивая совокупность формул, то логическим следствием совокупности А1,А2,….Ak|=B является формула В.
Исчисление высказываний. Для построения формализованной аксиоматической теории исчисления нужно: 1. Задать алфавит этой теории (т.е. конечную или счётную последовательность символов, в которых будет записана эта теория). 2. Среди всех слов в теории выделить формулы, т.е. слова которые будут являться формулами. 3. Среди формул выделить аксиомы, т.е. такие формулы из которых может быть построена вся теория. Они должны соответствовать тавтологиям в алгебре высказываний. 4. Определить правила получения новых формул из аксиом, т.е. правила вывода или правила доказательства теорем. Опр. Выводом (доказательством) формулы F из совокупности формул Г={Г1,Г2,…..,Гk} называется последовательность формул В1,В2,……Вn, в которых:
1. Последняя формула совпадает с выводимой формула Вn=F. 2. Каждая формула этой совокупности является либо аксиомой, либо одна из формул совокупности Г, либо получена из предыдущих с помощью правила вывода(Вi). Алфавит исчисления высказываний состоит из символов трех категорий: Формулы исчисления высказываний представляют собой последовательности символов алфавита исчисления высказываний. Для обозначения формул будем пользоваться большими буквами латинского алфавита. Эти буквы не являются символами исчисления. Они представляют собой только условные обозначения формул. Переменные высказывания будем называть элементарными формулами. Приведем примеры формул исчисления высказываний. Переменные высказывания являются формулами согласно п.1 определения формулы. Но тогда слова являются формулами согласно п.2 определения. По этой же причине будут формулами слова: Очевидно, не являются формулами слова: поскольку одни из них не взяты в скобки, в других скобка лишь одна,… Одновременно с понятием формулы вводится понятие подформулы или части формулы. 1. Подформулой элементарной формулы является она сама. 1. Если формула имеет вид, то ее подформулами являются: она сама, формула А и все подформулы формулы А. 2. Если формула имеет вид (А*В)(здесь и в дальнейшем под символом * будем понимать любой из трех символов), то ее подформулами являются: она сама, формулы А и В и все подформулы формул А и В. Таким образом, по мере “погружения вглубь структуры формулы” мы выделяем подформулы все большей глубины. Очевидно, что на самой большой глубине находятся лишь элементарные формулы. Однако элементарные формулы могут быть и на других глубинах. Введем в запись формул некоторые упрощения. Будем опускать в записи формул скобки по тем же правилам, что и в алгебре высказываний. Правило отделения в качестве правила вывода МР Из формулы x, x–›y можно отделить или выводима формула y (x,x–›y|-y) Утверждение1. Для любой формулы F исчисления высказываний формула |-(F–›F) (является теоремой, т.е. она доказуема, выводима из аксиом. Утверждение2. Если формула F является теоремой, то для любой формулы G, формула |-G–›F тоже является теоремой. Теорема дедукции. Следствие из теоремы дедукции. 1 Следствие: Формула G выводима из совокупности гипотез Г1,Г2,…..,Гk тогда и только тогда, когда из совокупности гипотез Г1,Г2,…..,Гk-1 выводима формула Гk –› G 2 Следствие: Формула G выводима из совокупности гипотез Г1,Г2,…..,Гk тогда и только тогда, когда (Г1 –›(Г2 –›….. –›(Гk-1 –›(Гk)….).
Законы логики.
1. правило силлогизма (цепного заключения) (А®В), (В®С) |-А®С Доказательство: 1) (А®(B®С))®(A®С) 2) А®(В®С)=u, т.к. В®С=u 3) А®С Итак, А®В, В®С|-А®С. Очевидно, т.к. А®С выводимо из А®В и В®С, то |= (А®В)(В®С)®(А®С) и |=(А®В) ® ((В®С)®(А®С)) 2. Правило перестановки посылок (А®(B®С)) |-(В–›(A®С)) Доказательство: 1) А®(B®С гипотеза 2) А гипотеза 3) В гипотеза 4) Из 2,1 МР В –› С 5) Из 3,4 МР С 3. Правило введения двойного отрицания А |- ⌐⌐А 4. Правило (А –›В) |-(⌐⌐А –›⌐⌐В) Доказательство: 1) А–›В гипотеза. 2) ⌐⌐А гипотеза. 3) Правило снятия двойного отрицания. 4) 2,3 МР А. 5) 4,1 МР В. 6) Правило введения двойного отрицания. 7) 5,6 МР ⌐⌐В 5. Второй закон контрапозиции А–›В|-(⌐В–›⌐А).
6. Первый закон контрапозиции ⌐В–›⌐А|-В–›А Доказательство: 1) ⌐В–›⌐А гипотеза 2) В гипотеза 3) А3. Y=A, X=B (⌐В–›⌐А) –›((⌐А–›В) –›А) 4) 1,3 МР (⌐А–›В) –›А 5) А1. X=B Y=⌐A (B–›(⌐A–›B) 6) 2,5 ⌐A–›B 7) 6,4 МР А 7. Первый закон противоречия А,⌐А|-В (|-А–›(⌐А–›В)) 8. Второй закон противоречия ⌐А–›В, А–› В |- В 9. Закон отрицания импликации А, ⌐В |- (⌐(А–›В)) (|-А–›(⌐В–›(⌐(А–› В)))) Полнота исчисления высказываний. Свойства полноты выражаются в том, что всякая тавтология является теоремой и обратно всякая теорема является тождественно истинной формулой алгебры высказываний. Теорема1. Всякая теорема исчисления высказываний является тавтологией. (если |- A, то |=A), (если А является теоремой, то она тождественно истинная). Теорема2. Любая тождественно истинная формула алгебры высказываний является теоремой исчисления высказываний. Если |=А’, то |-A Теорема3. Исчисление гипотез является полным. Непротиворечивость ИВ. Непротиворечивость ИВ. Определение. 1) ИВ противоречиво, если формула А выводима в немИВ непротиворечиво, если оно не является противоречивым.
Теорема: ИВ является непротиворечивым исчислением по отношению к любому из трех определений. Разрешимость ИВ. ИВ разрешима, если существует алгоритм, позволяющий устанавливать тождественную истинность формул. Алгебра предикатов. Операции над предикатами. Предикаты так же, как высказывания, могут принимать два значения: “истина” (1) и “ложь” (0), поэтому к ним применимы все операции логики высказываний, в результате чего из элементарных предикатов формируются сложные предикаты (как и в логике высказываний, где из элементарных высказываний формировались сложные, составные). Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов. Эти операции в логике предикатов сохраняют тот же смысл, который был им присвоен в логике высказываний. Пусть на некотором множестве M определены два предиката P(x) и Q(x). Определение 1. Конъюнкцией двух предикатов P(x) и Q(x) называется новый (сложный) предикат, который принимает значение “истина” при тех и только тех значениях, при которых каждый из предикатов принимает значение “истина”, и принимает значение “ложь” во всех остальных случаях. Очевидно, что областью истинности предиката является общая часть области истинности предикатов P(x) и Q(x), т.е. пересечение.
Так, например, для предикатов P(x): “x – четное число” и Q(x): “x кратно 3” конъюнкцией является предикат “x – четное число и x кратно трем”, т.е. предикат “x делится на 6”. Определение 2. Дизъюнкцией двух предикатов P(x) и Q(x) называется новый предикат, который принимает значение “ложь” при тех и только тех значениях, при которых каждый из предикатов принимает значение “ложь”, и принимает значение “истина” во всех остальных случаях. Определение 3. Отрицанием предиката P(x) называется новый предикат, который принимает значение “истина” при всех значениях, при которых предикат P(x) принимает значение “ложь”, и принимает значение “ложь” при тех значениях, при которых предикат P(x) принимает значение “истина”. Очевидно, что, т.е. множество истинности предиката является дополнением к множеству IP. Определение 4. Импликацией предикатов P(x) и Q(x) называется новый предикат, который является ложным при тех и только тех значениях, при которых одновременно P(x) принимает значение “истина”, а Q(x) – значение “ложь”, и принимает значение “истина” во всех остальных случаях. Поскольку при каждом фиксированном справедлива равносильность, то. Определение 5. Эквиваленцией предикатов P(x) и Q(x) называется новый предикат, который обращается в “истину” при всех тех и только тех, при которых P(x) и Q(x) обращаются оба в истинные или оба в ложные высказывания.
Классификация предикатов Определение 1. Предикат называется выполнимым, если существует набор предметов обращающий его в истинное высказывание или если его область истинности не является пустым множеством. Определение 2. Предикат Р(х), определенный на множестве М, называется тождественно истинным, если его множество истинности совпадает с областью определения, т. е. Ip=M. Определение 3. Предикат Р(х), определенный на множестве М, называется тождественно ложным, если его множество истинности является пустым множеством, т. е. Ip=0. Естественным обобщением понятия одноместного предиката является понятие многоместного предиката, с помощью которого выражаются отношения между предметами. Примером бинарного отношения, т. е. отношения между двумя предметами, является отношение “меньше ”. Пусть это отношение введено на множестве Z целых чисел. Оно может быть охарактеризовано высказывательной формой “х<y”, где, то–есть является функцией двух переменных Р(х,y), определенной на множестве упорядоченных пар целых чисел ZхZ=Z2 c множеством значений {1;0}. Определение 4. Предикат называется опровержимым, если существует набор предметов обращающий его в ложное высказывание. Операции связывания переменных кванторами. 1.1 Квантор всеобщности. Пусть Р(х) – предикат, определенный на множестве М. Под выражением понимают высказывание, истинное, когда Р(х) истинно для каждого элемента х из множества М, и ложное в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение звучит так: “Для всякого х Р(х) истинно ”.
Символ называют квантором всеобщности (общности). Переменную х в предикате Р(х) называют свободной ( ей можно придавать различные значения из М), в высказывании же х называют связанной квантором всеобщности. 1.2 Квантор существования. Пусть P(x) - предикат определенный на множестве М. Под выражением понимают высказывание, которое является истинным, если существует элемент, для которого P(x) истинно, и ложным – в противном случае. Это высказывание уже не зависит от x. Соответствующее ему словесное выражение звучит так: “Существует x, при котором P(x) истинно.” Символ называют квантором существования. В высказывании переменная x связана этим квантором (на нее навешен квантор). Кванторные операции применяются и к многоместным предикатам. Пусть, например, на множестве М задан двухместный предикат P(x,y). Применение кванторной операции к предикату P(x,y) по переменной x ставит в соответствие двухместному предикату P(x,y) одноместный предикат (или одноместный предикат), зависящий от переменной y и не зависящий от переменной x. К ним можно применить кванторные операции по переменной y, которые приведут уже к высказываниям следующих видов: Рассмотрим предикат P(x) определенный на множестве M={a1,…,an}, содержащем конечное число элементов. Если предикат P(x) является тождественно - истинным, то истинными будут высказывания P(a1),P(a2),…,P(an). При этом истинными будут высказывания и конъюнкция. Если же хотя бы для одного элемента P(ak)окажется ложным, то ложными будут высказывание и конъюнкция. Следовательно, справедлива равносильность Проблема разрешения. В алгебре высказываний эта проблема разрешается положительно,т.е. существует алгоритм, устанавливающий выполнимость формулы, этим алгоритмом является таблица истинности. В 1936 г. Американский математик А. Чёрч доказал, что не существует алгоритма, разрешающего установить алгебру предикатов. Для частных видов формул проблема решается полностью. Вид 1. Формулы, заданные на нечётных множествах. Пусть М={a1,a2,….an}- множество, заданное на конечном числе. Для F- формула на M возможны два варианта: а) либо формула F не содержит кванторов F(x1,……xm) б) либо формула F содержит кванторы. 2. в первом случае как решается проблема: Путём непосредственной подстановки в формулу значений предметных переменных. Каждая переменная может принимать n значений. Всего n*m наборов. Теорема: Если формула выполнима на каком либо множестве, то она выполнима на любом множестве с большим числом элементов.
Формализованное исчисление предикатов. Алфавит исчисления предикатов состоит из символов трех категорий: 3. Символы первой категории: Эти символы будем называть переменными высказываниями. 2. Символы второй категории: они носят общее название логических связок. Первый из них – знак дизъюнкции или логического сложения, второй – знак конъюнкции или логического умножения, третий – знак импликации или логического следования и четвертый – знак отрицания. 3. Третью категорию составляет пара символов (), называемая скобками. Других символов исчисление предикатов не имеет. Понятия вывода, теоремы определяются аналогично как в исчисление высказываний. Ф исчисление предикатов – независимая, полная, непротиворечивая, но разрешимой она не будет. Опр. Термом исчисления предикатов называется: 1) Отдельно взятые предметные переменные. 2) Если t1,t2,…tn термы, то f(t1,t2,…tn) терм, где f функциональный символ. Опр. Формулой исчисления предикатов называется 1) P(t1,t2,…tn), где ti- терм, Р- предметная буква. 2) Если F1,F2 формулы, то ⌐F1, (F1–›F2) формулы. Причём все переменные входящие в F1,F2 свободно, остаются свободными и в данных формулах. Формулы, в которых все переменные кроме x входят свободно. 3) Других формул нет! Замечание: Таким образом определённое исчисление предикатов называется исчислением первого порядка. Опр. Сигнатурой исчисления предикатов называется следующая совокупность символов ∂={c1,c2,…….cn, b1^c1…….,p1^j1…pn^jn…} Если сигнатура не содержит функциональных символов, то исчисление предикатов называется чистым исчислением предикатов. Замечание: F(x)- любая формула содержащая переменную x свободно и не находящейся под действием квантора по переменной t. F(t)- получена из F(x) заменой x на t. Опр. Выводом (доказательством) формулы F из совокупности формул Г={Г1,Г2,…..,Гk} называется последовательность формул В1,В2,……Вn, в которых: 1. Последняя формула совпадает с выводимой формула Вn=F. 2. Каждая формула этой совокупности является либо аксиомой, либо одна из формул совокупности Г, либо получена из предыдущих с помощью правила вывода, если (Вi) первая из формул, содержащая свободно, то в дальнейших формулах не может быть применимо правило конкретизации, или обобщения по переменной x. Опр. Интерпретацией формальной теории называется совокупность М, состоящая из множества предметов М<=M,m- арных операций на М P1^m,…..Pn^m. Интерпретация называется моделью формул этой теории, если любая формула в данной интерпретации тождественно истинна. Теорема: Если в модели М выполняются все формулы совокупности Ф и из совокупности формул Ф выводима F Ф|-F, то формула F выполняется в модели М.
Примеры численных алгоритмов. Основные черты алгоритмов. Необходимость уточнения понятия алгоритмов
Понятие алгоритма принадлежит к числу основных понятий математики. Первые примеры алгоритмов встречаются в средней школе. Примерами таких алгоритмов являются: а) алгоритм сложения двух натуральных чисел, записанных в десятичной системе счисления; б) алгоритм вычитания; в) алгоритм умножения двух натуральных чисел; г) алгоритм Евклида; д) алгоритм разложения натурального числа на простые множители; е) алгоритм извлечения квадратного корня из натурального числа и т.д. Разбор этих примеров позволяет заключать, что каждый из этих алгоритмов представляет собой точное предписание, определяющую вполне определенную последовательность простейших действий, осуществляя которые мы либо никогда не закончим процесс вычислений, либо этот процесс заканчивается и мы получаем объект(число в наших примерах), либо процесс обрывается без получения результата. Это описание лежит в основе интуитивного представления алгоритма. Характерные черты алгоритмов: 1. Дискретность; 2. Детерминированность; 3. Элементарность шагов; 4. Направленность; 5. Массовость. На практике интуитивного представления об алгоритме бывает достаточно, чтобы установить, является ли данное предписание алгоритмом или нет. Есть задачи, для решения которых не существует эффективного алгоритма. В этих случаях без уточнения, без формализации понятия алгоритма обойтись нельзя. Примеры. Возможные уточнения понятия алгоритм: теория частично-рекурсивных функций, машина Тьюринга, нормальные алгоритмы Маркова.
Формальная теория вычислимости. Исходные функции. Частично рекурсивные функции. Рекурсивные предикаты Простейшие функции: Основные вычислительные операторы: оператор суперпозиции частичных функций, оператор примитивной рекурсии. Примитивно рекурсивные функции. Примеры примитивно рекурсивных функций. Оператор минимизации. Частично рекурсивные функции. Общерекурсивные функции. Рекурсивные предикаты. Пусть Р – n- местный предикат на множестве натуральных чисел N. Функция Определение: Предикат Р называется рекурсивным (примитивно рекурсивным) если его характеристические функция общерекурсивна(примитивно рекурсивна).
Логические операции над предикатами. Ограниченные кванторы. Постановка функции в предикат. Кусочное задание функции Над предикатами, заданными на множестве натуральных чисел N будем использовать операции отрицания (), конъюнкции(^), дизъюнкции(
Например, запись Теорема. Предикаты, которые можно получить из примитивно рекурсивных(или рекурсивных) с помощью логических операций и ограниченных кванторов также примитивно рекурсивны (соотв. рекурсивны). Подстановка функции в предикат используется при доказательстве примитивной рекурсивности функций, заданных кусочно. Определение: функция
При этом предполагается, что для каждого набора Теорема. Если функции
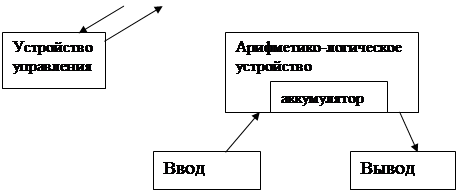
Компьютер фон Неймана Архитектура Эккерта – фон Неймана и концепция хранимой программы. Историческая справка. Описание машины фон – Неймана. Машина фон – Неймана представляет собой вычислительную систему, построенная на следующих принципах: 1. основными ее блоками является арифметико-логическое устройство, устройство управления, запоминающее устройство и устройство ввода-вывода. 2. Программы и данные хранятся в одной и той же памяти. 3. Устройство управления и арифметико-логическое устройство, обычно объединенные в центральный процессор, определяют действия, подлежащие выполнению путем считывания команд из оперативной памяти. 4. Внутренний код машины двоичен. Подавляющее большинство вычислительных машин(компьютеров) в настоящее время является фон-неймановскими машинами. Свое название эта архитектура получила в честь американского ученого Джона фон Неймана (von Neumann). В литературе эта точка зрения воспринимается неоднозначно.
Архитектура машины фон – Неймана.
Алгебра высказываний. Формулы алгебры высказываний. Высказывание - это повествовательное предложение, о котором можно судить истинно оно или ложно. Безличные предложения и вопросительные не являются высказываниями. Пример: Снег чёрный – высказывание. Два умножить на два, равно пять – высказывание. 3<9 высказывание. Добро пожаловать! – не высказывание. Высказывания обозначаются заглавными буквами латинского алфавита A,B,C,R,….,S. A: “3>2” Если высказывание истинно, то значение истинности |A|=1. Если высказывание ложно, то |B|=0. Операции над высказываниями Отрицанием высказывания P называется такое высказывание, обозначаемое ⌐P (не P), которое ложно, если P- истинно, и ложно в противном случае. Конъюнкцией высказываний P и Q называется такое высказывание, обозначаемое P^Q, которое истинно, тогда и только тогда, когда P и Q истинно одновременно. Дизъюнкцией высказываний P и Q называется такое высказывание, обозначаемое PÚQ, которое ложно, тогда и только тогда, когда P и Q ложно одновременно. Импликацией высказываний P и Q называется такое высказывание, обозначаемое P–›Q, которое ложно, тогда и только тогда, когда P истинно, а Q ложно. Эквиваленцией высказываний P и Q называется такое высказывание, обозначаемое P‹–›Q, которое истинно, тогда и только тогда, когда P и Q принимают одинаковые значения истинности. Формулы алгебры высказывания Переменные, вместо которых можно подставлять высказывания, называются пропозиционными переменными.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.125.7 (0.142 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||
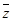 формула алгебры высказываний.
формула алгебры высказываний.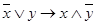 таблица истинности имеет вид:
таблица истинности имеет вид: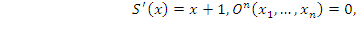
 называется характеристической для предиката Р, если эта функция удовлетворяет условиям
называется характеристической для предиката Р, если эта функция удовлетворяет условиям 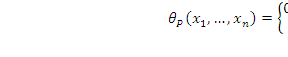
 , импликации(→) и эквивалентности, а также ограниченные кванторы:
, импликации(→) и эквивалентности, а также ограниченные кванторы: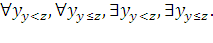
 означает предикаты «для любого у такого, что y<z и
означает предикаты «для любого у такого, что y<z и  ».
». называется кусочно заданной, если она удовлетворяет условиям:
называется кусочно заданной, если она удовлетворяет условиям: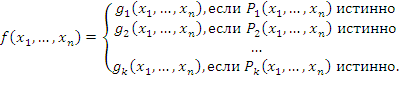
 значений переменных истинно одно и только одно из высказываний
значений переменных истинно одно и только одно из высказываний 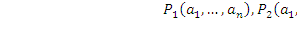 .
. и предикаты
и предикаты  примитивно рекурсивны (рекурсивны), то функция
примитивно рекурсивны (рекурсивны), то функция