Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цифровая модель рельефа (ЦМР)
Исходные данные: набор точек Отображение – упорядоченный набор точек
Он проходит через все точки набора. Недостатки: 1. Значение высоты в заданной точке зависит от всех остальных точек, то есть нет локальности; 2. Плохо удалять и добавлять точки, так как это приводит к перестройке всего многочлена. 2. Долго вычислять. Достоинство: прост в построении. Рассмотрим модели рельефа: Существует два способа построения ------Билет 13. GRID-модель рельефа. Алгоритмы построения GRID-моделей ------ GRID- модели – модели регулярных ячеек.
Пусть введена система координат
Вычисляем
Нормировочный коэффициент: Чем
Это метод IDW – долгий, для каждой т. необходимо найти соседей. Набор соседей может быть эффективно найден - ближайшим. Каждая из точек продуцирует «колышек» определенной высоты. От нерегулярности постановок точки многое зависит, для этого берут Преимущество – простота Недостаток: 1) На значение высоты влияет набор точек. Чтобы этого избежать, матрицу разбивают на сектора и вводят коэффициенты 2) ------Билет 14. TIN-модель. Алгоритмы триангуляции Делоне ------ Триангуляционные (TIN). Триангуляция – построение функции в виде совокупности кусочно - линейной функции
Триангуляция – интерполяция внутри выпуклой области. Триангуляция – планарный граф, все внутренние ребра которого – треугольники; способ представления пространства в виде примыкающих друг к другу треугольников без перекрытий. На наборе точек триангуляция строится несколькими способами.
Нужен алгоритм для построения оптимальной триангуляции.
Плоскость, проходящая через 3 точки.
1) Найдем треугольник, который 2) Чтобы проверить находятся ли точки внутри треугольника или нет, необходимо подставить значение в уравнение линий – ребер треугольника. Если все 3 уравнения > 0, то внутри. Структура представления: Каждая триангуляция содержит одинаковое количество треугольников.
Жадный триангуляция. Все точки соединяем ребрами, выбираем минимум, добавляем в триангуляцию. Далее берем следующий минимум, не пересекающийся с предыдущими и т.д. В результате получена жадная триангуляция. Триангуляция Делоне. Внутрь окружности, описанной вокруг любого треугольника, не попадают точки других треугольников. Строится единственным образом.
Флипом называется переброска ребер. Она позволяет перейти от обычной триангуляции к триангуляции Делоне. Чтобы проверить принадлежность точки к окружности: подставить, если < R, то внутри. Условие Делоне. Уравнение окружности, проходящей через три точки:
Если меньше нуля, то внешняя, иначе – внутренняя.
Алгоритм построения триангуляции Делоне: 1) Подследственного добавления точек – простой итеративный алгоритм: Есть набор Теоретическая сложность 2) Методы ускорения. Основан на статистически зависимых точках. Затравочный треугольник – треугольник в который попала предыдущая точка. Затем соединяем две точки – предыдущую и новую. Перемещаемся из первой точки в другую.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.29 (0.009 с.) |
 ,
,  , расположенных нерегулярно, тогда надо строить интерполяционную (иногда экстраполяционную) поверхность
, расположенных нерегулярно, тогда надо строить интерполяционную (иногда экстраполяционную) поверхность 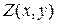 ,
, 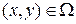 .
. , т.к. поверхность может быть построена по какому то критерию. Обычно строят кривые по данным точкам изначально сплайнами или интерполяционно. Берем вместо
, т.к. поверхность может быть построена по какому то критерию. Обычно строят кривые по данным точкам изначально сплайнами или интерполяционно. Берем вместо  полином Лагранжа:
полином Лагранжа:
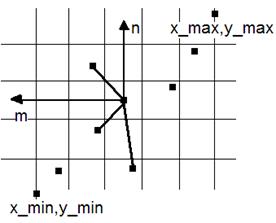
 и
и  и
и  . Пользователь задает
. Пользователь задает  и шаги дискретизации
и шаги дискретизации  .
.
 ,
, 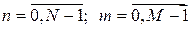
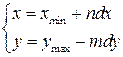 - физические координаты точки.
- физические координаты точки.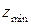 и
и  ,
, 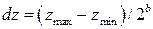 - разрядная сетка.
- разрядная сетка. - квантованные значения. Реальные:
- квантованные значения. Реальные: 

 - параметр алгоритма – количество точек,
- параметр алгоритма – количество точек,  - вес. Чем ближе точка, тем больше вес.
- вес. Чем ближе точка, тем больше вес.
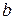 - степень расстояния (1 или 2).
- степень расстояния (1 или 2).

 или
или 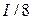 т.е. разделяют на сектора и в окрестности точки строим.
т.е. разделяют на сектора и в окрестности точки строим. или
или 
 – локальные экстремумы построенной функции.
– локальные экстремумы построенной функции.



 ;
; , где
, где  – количество точек.
– количество точек.
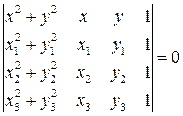

 – условие Делоне.
– условие Делоне.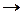 добавляем в треугольник, осуществляется построение
добавляем в треугольник, осуществляется построение