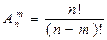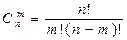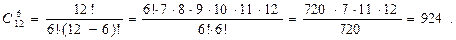Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Дифференциальное и интегральное исчисление
ВВЕДЕНИЕ
Учебная дисциплина Математика предназначена для реализации Федерального государственного образовательного стандарта (далее – ФГОС) по специальности среднего профессионального образования (далее - СПО) к минимуму содержания и уровню подготовки выпускников колледжа по специальности 26.02.03 Судовождение, входящей в состав укрупненной группы специальностей 26.00.00 Техника и технологии кораблестроения и водного транспорта, базовой подготовки. Дисциплина Математика - обязательная дисциплина математического и общего естественнонаучного цикла (ЕН.01). В ходе изучения дисциплины Математика рассматриваются следующие основные разделы:
Раздел 1. Дифференциальное и интегральное исчисление | ||||||||||||||||||||||||||||||||||||||||||
| 1 | Функция одной независимой переменной. Пределы. | ||||||||||||||||||||||||||||||||||||||||||
| 2 | Производная и ее геометрический смысл. Применение производной. | ||||||||||||||||||||||||||||||||||||||||||
| 3 | Дифференциал функции и его применение в приближенных вычислениях. | ||||||||||||||||||||||||||||||||||||||||||
| 4 | Первообразная. Неопределенный интеграл. Способы вычисления неопределенного интеграла. | ||||||||||||||||||||||||||||||||||||||||||
| 5 | Определенный интеграл, методы его вычисления. | ||||||||||||||||||||||||||||||||||||||||||
| 6 | Геометрический смысл определенного интеграла. | ||||||||||||||||||||||||||||||||||||||||||
| 7 | Применение определенного интеграла к решению прикладных задач. | ||||||||||||||||||||||||||||||||||||||||||
|
Раздел 2. Основные численные методы | |||||||||||||||||||||||||||||||||||||||||||
| 1 | Численное интегрирование. Вычисление интегралов по формулам прямоугольников, трапеций, формуле Симпсона. | ||||||||||||||||||||||||||||||||||||||||||
| 2 | Численное дифференцирование. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона. | ||||||||||||||||||||||||||||||||||||||||||
|
Вычислите пределы: 1. а) 3. а) 5. а) 7. а) 9. а) 11. - 20. Найдите производную функции: 11. y = ln2cosx. 12. y = 16. y = 21. - 22. Найдите вторую производную функции: 21. y = x∙lnx – x. 22. y = 5∙lnx + x. 23.-28. Задачи на приложения производной: 23. Составьте уравнение касательной к графику 24. Составьте уравнение нормали к графику
25. Тело движется прямолинейно по закону s= 3 + 9t + 3t 26. Тело движется прямолинейно по закону s= t3- 4t2 + 5. Найдите ускорение движения тела в момент времени t=2 сек. 27. Найдите интервалы монотонности функции: у = 28. Найдите интервалы выпуклости и вогнутости функции: у = 29.-30. Найдите дифференциал функции: 29. y = 31.-40. Найдите интегралы: 31. а) 33. а) 35. а) 37. а) 39. а) 41.- 50. Вычислите интеграл: 41. 46. 50. Задачи на применение определенного интеграла: 51. Вычислите площадь фигуры, ограниченной линиями: 52. Вычислите площадь фигуры, ограниченной линиями: 53. Вычислите площадь фигуры, ограниченной линиями: 54. Вычислите площадь фигуры, ограниченной линиями: 55. Вычислите площадь фигуры, ограниченной осью Ох и линией 56. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:
57. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:
58. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: 59. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: 60. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:
61. – 70. Решите дифференциальное уравнение и найдите частное решение: 61. 63. 65. 67. 69. 71. - 80. Найдите общее решение дифференциального уравнения: 71. 76. 81. – 90. Исследуйте на сходимость ряд: 81.
86. Формулы дифференцирования
Правила дифференцирования 1) с' = 0, – производная постоянной функции, 2) х' = 1 – производная от х по аргументу х, 3) (u+v-w)' = u' + v' - w' – производная алгебраической суммы, 4) (u∙v)' = u'∙v + u∙v' – производная произведения 5) (c∙ u)' = c∙u' – постоянный множитель можно выносить за знак производной, 6) Производные высших порядков Пример: Найти производную второго порядка от функции f(x)=x4. Решение: f'(x)=(x4)' =4x3 f''(x)=(f'(x))'=(4 x3)'=4=3 x2=12 x2 Ответ: f''(x)=12x2 Производная третьего порядка определяется аналогично - как производная от второй производной, т.е. все тоже последовательное дифференцирование. Например, третья производная от функции из предыдущего примера будет: f'''(x =24 x Дадим строгое определение производной старшего порядка: Производной n-ого порядка f(n)(x) называется производная от производной (n-1)-го порядка. Приложения производной. 5.1. Геометрический смыл производной: Рассмотрим график функции y = f (x). Из рисунка 1 видно, что для любых двух точек A и B графика функции: Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A, т.е. Найдите интегралы: Пример 1 Решение: Пример 2. ∫e-x3x2dx Подстановка: -x3=t, -3x2dx=dt, Решение: ∫e-x3x2dx=∫et(-1/3)dt=-1/3et+C=-1/3e-x3+C Пример 3. Решение: Тема 1. Комбинаторика П.1 Понятие факториала Произведение всех натуральных чисел от 1 до n включительно называют n -факториалом и пишут: n!=1·2·3·…·(n-1)·n Вычислить: 3! Решение: 3!=1·2·3=6 п.2 Перестановки Определение: Комбинации из n элементов, которые отличаются друг от друга только порядком элементов называются перестановками или Установленный в конечном множестве порядок называется перестановкой его элементов. Число перестановок из n элементов обозначается Рn, их вычисляют по формуле: Рn = n·(n-1)·(n-2)·…·3·2·1 или с помощью факториала: Рn = n! Следствия: Р0=1! =1; Р1=1!=1 Пример: Сколькими способами можно рассадить 10 гостей по десяти местам за праздничным столом? Решение: Искомое число способов равно числу перестановок из 10 элементов: Р10 = 10! = 3 628 800 П.3 Размещения Определение: Комбинация из n элементов по m элементов, которые отличаются друг от друга или самими элементами или порядком элементов, называются размещениями.
Число размещений обозначается и вычисляется по формуле:
Пример: Перед выпуском группа студентов в 30 человек обменялась фотокарточками. Сколько всего было роздано фотокарточек? Решение: Передача фотокарточек одним студентом другому есть размещение из 30 элементов по 2 элемента:
- число размещений равно 870. П.4 Сочетания Определение: Сочетаниями называются все возможные комбинации из n элементов по m, которые отличаются друг от друга по крайней мере хотя бы одним элементом (здесь m и n - натуральные числа, причем m ≤ n). Число сочетаний обозначается и вычисляется по формуле: Пример: Сколькими способами можно распределить 12 человек по бригадам, если в каждой бригаде по 6 человек? Решение: Состав каждой бригады является конечным множеством из 12 элементов по 6. Значит, искомое число способов равно числу сочетаний из 12 элементов по 6 в каждом:
Тема 2. Основные понятия теории вероятности 1. Основные понятия и определения Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием. Например, многократное подбрасывание монеты, процесс изготовления какой-либо детали представляют собой испытания. Результатом этого действия или наблюдения будем называть случайным событием. Например, появление цифры при подбрасывании монеты является случайным событием, поскольку оно могло произойти или не произойти. Если вас интересует какое-либо определенное событие из всех возможных событий, то будем называть его искомым событием (или искомым исходом). Все рассматриваемые события будем считать равновозможными, т. е. такими, которые имеют равные возможности произойти. События принято обозначать заглавными буквами латинского алфавита: A, В, С, D. События называются несовместными, если никакие два из них не могут произойти в данном опыте вместе. В противном случае называются совместными. Так при подбрасывании монеты появление цифры исключает одновременное появление герба; это – пример несовместимых событий. Событие называется достоверным, если оно происходит в данном испытании обязательно. Например, выигрыш по билету беспроигрышной лотереи есть событие достоверное.
Событие называется невозможным, если оно в данном опыте не может произойти. Например, при бросании игральной кости невозможно получить 7 очков. Полной системой событий А1, А2, А3, …, Аn называется совокупность несовместных событий, наступление хотя бы одного из которых обязательно при данном испытании. Так, выпадение одного, двух, трех, четырех, пяти или шести очков при бросании игральной кости есть полная система событий, поскольку все эти события несовместны и наступление хотя бы одного из них обязательно. Если полная система состоит из двух событий, то такие события называются противоположными и обозначаются А и Ā. ВВЕДЕНИЕ
Учебная дисциплина Математика предназначена для реализации Федерального государственного образовательного стандарта (далее – ФГОС) по специальности среднего профессионального образования (далее - СПО) к минимуму содержания и уровню подготовки выпускников колледжа по специальности 26.02.03 Судовождение, входящей в состав укрупненной группы специальностей 26.00.00 Техника и технологии кораблестроения и водного транспорта, базовой подготовки. Дисциплина Математика - обязательная дисциплина математического и общего естественнонаучного цикла (ЕН.01). В ходе изучения дисциплины Математика рассматриваются следующие основные разделы:
Раздел 1. Дифференциальное и интегральное исчисление
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 44; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.2.34 (0.09 с.) |
|||||||||||||||||||||||||||||||||||||||||||
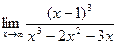 ; б)
; б) 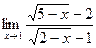 . 2. а)
. 2. а) 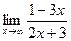 ; б)
; б) 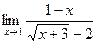 .
.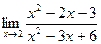 ; б)
; б) 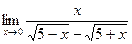 . 4. а)
. 4. а) 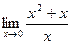 ; б)
; б) 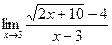 .
.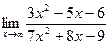 ; б)
; б) 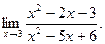 6. а)
6. а) 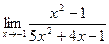 ; б)
; б) 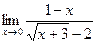 .
. ; б)
; б)  ; б)
; б) 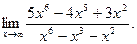
 ; б)
; б) 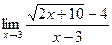 . 10. а)
. 10. а) 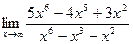 ; б)
; б) 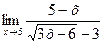 .
.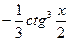 . 13. y =
. 13. y = 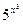 . 14. y=
. 14. y= 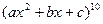 . 15. y=
. 15. y= 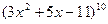 .
.  . 17. y =
. 17. y = 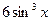 . 18. y =
. 18. y =  . 19. y =
. 19. y =  . 20. y =
. 20. y = 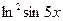 .
. в точке с абсциссой х = -2.
в точке с абсциссой х = -2. +
+  . Найдите ускорение движения тела в конце 3 секунды.
. Найдите ускорение движения тела в конце 3 секунды.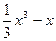 .
.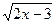 - дифференциал первого порядка, 30. y = x∙lnx –7x - дифференциал второго порядка.
- дифференциал первого порядка, 30. y = x∙lnx –7x - дифференциал второго порядка.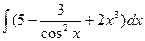 ; б)
; б) 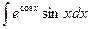 . 32. а)
. 32. а) 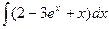 ; б)
; б) 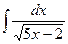 .
. ; б)
; б) 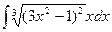 . 34. а)
. 34. а)  ; б)
; б)  .
. ; б)
; б) 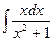 . 36. а)
. 36. а)  ; б)
; б) 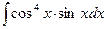 .
. ; б)
; б) 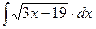 . 38. а)
. 38. а) 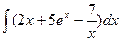 ; б)
; б) 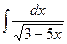 .
.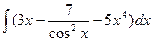 ; б)
; б)  . 40. а)
. 40. а)  ; б)
; б)  .
.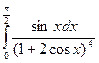 . 42.
. 42. 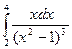 . 43.
. 43.  . 44.
. 44. 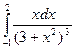 . 45.
. 45. 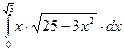 .
. . 47.
. 47. 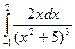 . 48.
. 48. 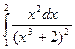 . 49.
. 49.  . 50.
. 50. 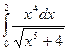 .
. 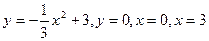 .
. .
.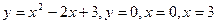 .
.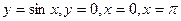 и осью Ох.
и осью Ох.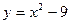 .
.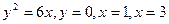 .
.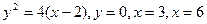 .
.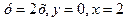 .
. .
.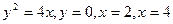 .
.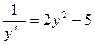 , при x=-4 y=1. 62.
, при x=-4 y=1. 62. 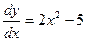 , y =4 при x= 0.
, y =4 при x= 0.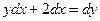 , y=3 при х=0. 64.
, y=3 при х=0. 64.  , y=7 при х=0.
, y=7 при х=0.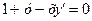 , у=3 при х=1. 66.
, у=3 при х=1. 66. 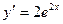 , y = 6 при x = 0.
, y = 6 при x = 0.  , y=1 при x=2. 68.
, y=1 при x=2. 68.  ; y=1 при x= -1.
; y=1 при x= -1.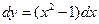 ; y=4 при x=1. 70.
; y=4 при x=1. 70. 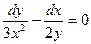 , у=4 при х=2.
, у=4 при х=2.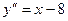 . 72.
. 72.  . 73.
. 73.  . 74.
. 74. 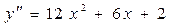 . 75.
. 75. 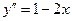 .
.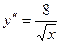 . 77.
. 77. 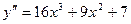 . 78.
. 78. 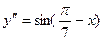 . 79.
. 79. 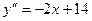 . 80.
. 80. 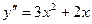 .
. . 82.
. 82. 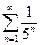 . 83.
. 83.  . 84.
. 84. 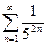 . 85.
. 85. 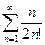 .
.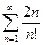 . 87.
. 87.  . 88.
. 88.  . 89.
. 89.  . 90.
. 90. 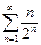
 ,
,
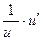 ,
,
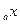 )' =
)' = 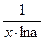 ,
,
 )'=
)'= 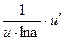 ,
,
 ,
,
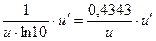 ,
,
 )' =
)' = 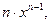
 )'=
)'= 
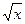 )' =
)' = 
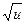 )' =
)' = 
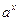 )' =
)' =  6* (ех)' = ех
6* (ех)' = ех
 )' =
)' =  (е u)' = е u ∙ u',
(е u)' = е u ∙ u',
 )' = cosx,
)' = cosx,
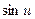 )' = cos
)' = cos 
 )' = - sinx,
)' = - sinx,
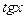 )' =
)' = 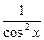 ,
,
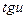 )' =
)' =  ,
,
 )' =
)' =  ,
,
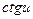 )' =
)' =  ,
,
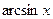 )' =
)' = 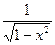 ,
,
 )' =
)' =  ,
,
 )' = -
)' = - 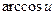 )' = -
)' = - 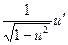 ,
,
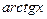 )' =
)' = 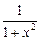 ,
,
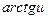 )' =
)' = 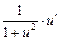 ,
,
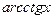 )' = –
)' = –  )' = -
)' = - 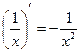
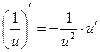
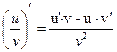 – производная частного.
– производная частного.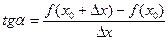 , где α - угол наклона секущей AB.
, где α - угол наклона секущей AB.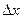 неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. . Отсюда следует: Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, т.е.
. Отсюда следует: Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, т.е.  .
.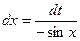

 Подстановка: 1+sinx=t, cosxdx=dt,
Подстановка: 1+sinx=t, cosxdx=dt,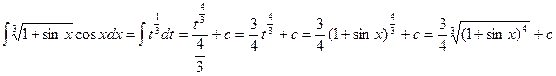 .
.