Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 13. Итоговое повторение курса математикиСтр 1 из 4Следующая ⇒
Г.
Раздел 13. Итоговое повторение курса математики
Тема 13.9. Многогранники. Площадь поверхностей многогранников
Правильная призма. Параллелепипед. Куб Если через каждую точку плоской ломанной провести прямые, параллельные данному направлению, не параллельную плоскости ломанной, то получим бесконечную призматическую поверхность. Если провести через каждую точку многоугольника прямые, параллельные данному направлению, не параллельному плоскости, то получим бесконечную призму. Любые две параллельные плоскости, отсекают от неё многогранник, называемый призмой. Части параллельных плоскостей называются основаниями призмы. Боковые грани представляют собой параллелограммы, а их объединение – боковую поверхность. Общие стороны параллелограммов называют боковыми ребрами призмы, а стороны основания называют ребрами основания. Призмы называются треугольными, четырехугольными, пятиугольными, n- угольными в зависимости от числа вершин многоугольника, лежащего в основании. Отрезок, соединяющий две вершины не лежащие в одной грани, называется диагональю призмы. Число диагоналей призмы n(n-3). Плоскость, проходящая через два боковых ребра призмы, не лежащих на одной грани, называется диагональной плоскостью. Отрезок перпендикуляра, проведенный из любой точки верхнего основания на плоскость нижнего основания называется высотой призмы. Призма, боковые ребра которой перпендикулярны плоскости оснований, называется прямой. Если боковые ребра призмы не перпендикулярны плоскостям оснований, то призма называется наклонной. Прямая призма, основанием которой является правильный многоугольник, называется правильной. Проекция оснований призмы на плоскость, перпендикулярную ребрам, называется перпендикулярным сечением призмы. Теорема: Площадь боковой поверхности призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра призма, т.е. Призму, в основании которой находится параллелограмм, называют параллелепипедом. Параллелепипед, у которого боковые ребра перпендикулярны плоскости основания, называют прямым. У прямого параллелепипеда боковые грани прямоугольники.
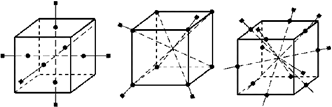
Прямой параллелепипед, у которого основания – прямоугольники, называют прямоугольным параллелепипедом. У прямого параллелепипеда все грани – прямоугольники. Прямоугольный параллелепипед, у которого три ребра, выходящие из одной точки равны, называется кубом. Симметрия куба 1. Центр симметрии — центр куба (точка пересечения диагоналей куба).
2. Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер; шесть плоскостей симметрии, проходящие через противолежащие ребра.
3. Оси симметрии: три оси симметрии, проходящие через центры противолежащих граней; четыре оси симметрии, проходящие через противолежащие вершины; шесть осей симметрии, проходящие через середины противолежащих ребер.
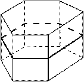
Симметрия параллелепипеда
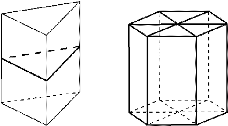
Симметрия прямой призмы Плоскость симметрии, проходящая через середины боковых ребер.
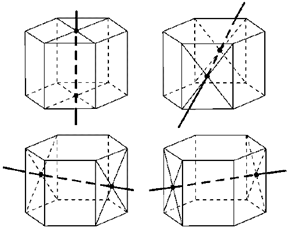
Симметрия правильной призмы 1. Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной призмы:
2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон основания — плоскости, проходящие через противолежащие ребра.
3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через центры оснований, и оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней.
Правильный Многогранник |
Число | ||||||||
| граней | вершин | рёбер | ||||||||
| Тетраэдр | 4 | 4 | 6 | |||||||
| Куб | 6 | 8 | 12 | |||||||
| Октаэдр | 8 | 6 | 12 | |||||||
| Додекаэдр | 12 | 20 | 30 | |||||||
| Икосаэдр | 20 | 12 | 30 | |||||||
Шар
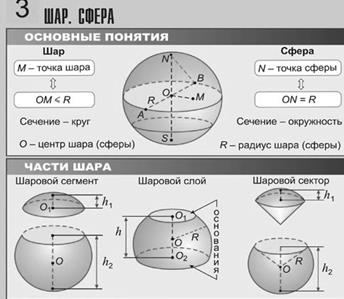
Вписанный и описанный шар
Определения:
1. Шар называется вписанным в многогранник, а многогранник описанным около шара, если поверхность шара касается всех граней многогранника.
2. Шар называется описанным около многогранника, а многогранник вписанным в шар, если поверхность шара проходит через все вершины многогранника.
|
|
3. Шар называется вписанным в цилиндр, усеченный конус (конус), а цилиндр, усеченный конус (конус) – описанным около шара, если поверхность шара касается оснований (основания) и всех образующих цилиндра, усеченного конуса (конуса).
4. Шар называется описанным около цилиндра, усеченного конуса (конуса), если окружности оснований (окружность основания и вершина) принадлежат поверхности шара.
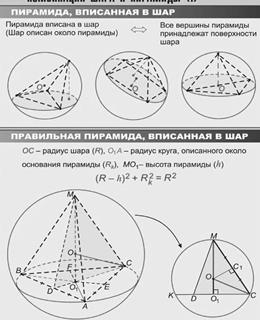
Комбинация шара с призмой
Теорема 1. Шар можно вписать в прямую призму, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
Теорема 2. Шар можно описать около призмы, если призма прямая и около ее основания можно описать окружность.
Комбинация шара с пирамидой
 Теорема 3. Около пирамиды можно описать шар, если около ее основания можно описать окружность.
Теорема 3. Около пирамиды можно описать шар, если около ее основания можно описать окружность.
Теорема 4. Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.
Г.
Раздел 13. Итоговое повторение курса математики
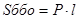 .
.
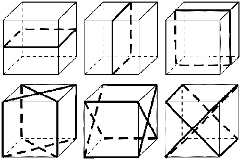
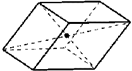 Центр симметрии — точка пересечения диагоналей параллелепипеда.
Центр симметрии — точка пересечения диагоналей параллелепипеда.