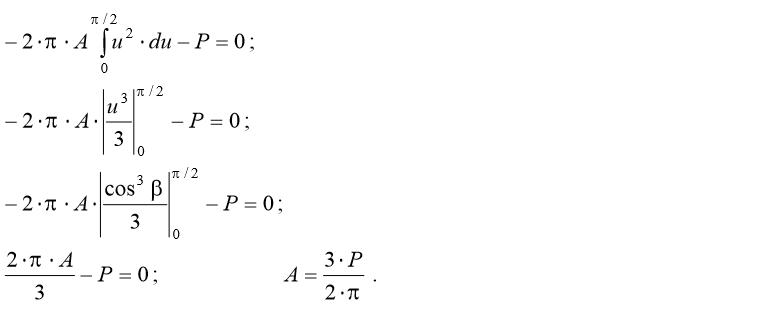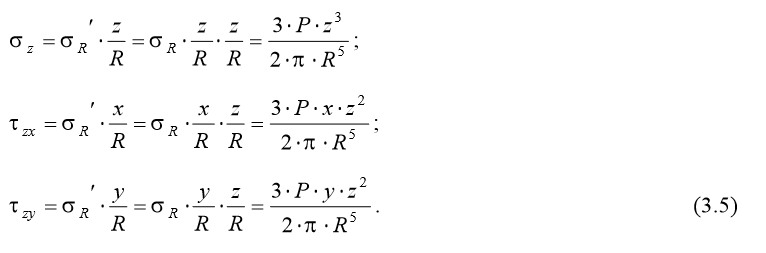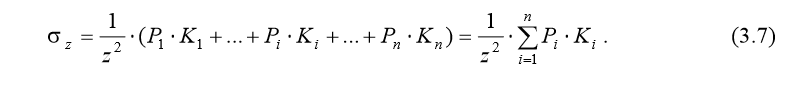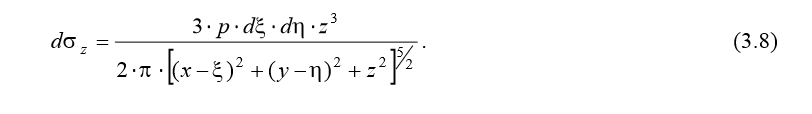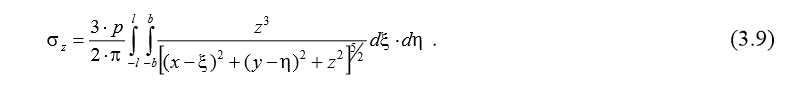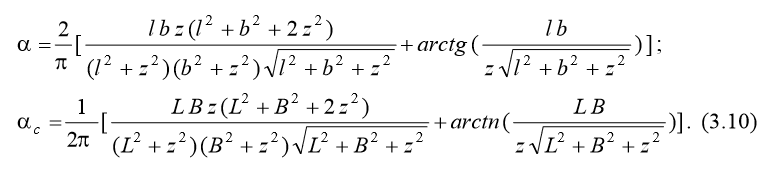Лекция 3. Распределение напряжений в грунтовом массиве от действия внешних нагрузок. Задача Ж. Буссинеска и ее приложения.

Проблемы распределения напряжений в грунтовом массиве рассматриваются в фазе его уплотнения. Как уже отмечалось, фаза уплотнения является стадией его напряженно-деформированного состояния, представляющей наибольший интерес для практики, так как при реальном проектировании напряжения в грунтовом массиве ограничиваются величиной, незначительно превышающей начальное критическое давление. Важнейшим следствием принципа линейной деформируемости, применимость которого находится в диапазоне напряжений, соответствующих фазе уплотнения, является правомерность использования для анализа напряженнодеформированного состояния грунтового массива аппарата теории упругости. При этом в указанном анализе модуль упругости должен быть заменен на модуль деформации, комплексно учитывающий развитие как упругих, так и пластических деформаций грунта. В общем случае задача о распределении напряжений в грунтовом массиве при заданных краевых условиях может быть сведена к решению дифференциальных уравнений равновесия, дополненных уравнениями совместности деформаций и физическими уравнениями в форме закона Гука. Такие задачи, как правило, решаются численными методами, так как получение для них замкнутых аналитических решений является весьма проблематичным (подынтегральные функции не являются, как правило, полными дифференциалами). По этой причине представляют особый практический интерес аналитические решения, полученные с использованием только уравнений равновесия на основании упрощающих гипотез. К таким решениям относится широко известная в механике грунтов задача Буссинеска о распределении напряжений в упругом полупространстве от действия вертикальной сосредоточенной силы на граничной плоскости. Представляют практический интерес не столько решения указанной задачи, сколько ее приложения. Используя принцип суперпозиций, решены задачи о распределении напряжений в грунтовом массиве при произвольной нагрузке на граничной плоскости полупространства, основанные на интегрировании решения Буссинеска. Такое же значение в механике грунтов имеет задача Фламана о распределении напряжений в полуплоскости при действии вертикальной силы на ее границе в условиях отсутствия деформаций, нормальных полуплоскости (такое напряженно–деформированное состояние называется «плоская деформация»).

Примечание: полупространством называют часть бесконечного (трехмерного) пространства, отсеченного бесконечной плоскостью; полуплоскостью называют часть бесконечной плоскости, отсеченной бесконечной линией (границей).

1. Решение задачи Буссинеска. Основано на следующих гипотезах (в последствии подтвержденных точными решениями):

а) нормальные напряжения на площадках, касательных к сферической поверхности с центром в точке приложения силы, являются главными напряжениями. По этой причине касательные напряжения на указанных площадках отсутствуют;

б) нормальные напряжения, лежащие в вертикальной плоскости, на площадках, нормальных к сферической поверхности с центром в точке приложения силы, равны нулю;

в) нормальные напряжения на площадках, касательных к сферической поверхности с центром в точке приложения силы, прямо пропорциональны косинусу угла видимости и обратно пропорциональны квадрату радиуса сферы. Под углом видимости понимается угол между радиусом сферы, проведенным в центр площадки, и центральной вертикальной осью сферы.

Постулированные гипотезы позволяют получить замкнутые аналитические решения о распределении напряжений в полупространстве от действия вертикальной силы на его границе, основанные исключительно на уравнениях равновесия. Решение задачи поясняется графическими построениями на рис. 3.1, на котором представлены вертикальный разрез полупространства и его сечения горизонтальными плоскостями.

Начало прямоугольной декартовой системы координат разместим в точке приложения вертикальной силы Р на границе полупространства. Ось z направим по вертикали вниз, ось x по горизонтали вправо, а ось y перпендикулярно плоскости чертежа. Относительно начала осей координат построена полусфера радиусом R, пересечение которой с вертикальной плоскостью, проходящей через центральную ось, образует полуокружность такого же радиуса. В сечении полусферы горизонтальной плоскостью на глубине z образуется окружность радиусом r. Угол видимости радиуса r на вертикальном разрезе обозначим β. В сечение полусферы горизонтальной 

Рис

. 3.1.

Графическое

построение

к

решению

задачи

Буссинеска

.

dz

 

плоскостью на глубине z – dz образуется окружность радиусом r + dr с углом видимости на вертикальном разрезе β + d β. Рассмотрим равновесие сферического кольца, выделенного из полусферы двумя горизонтальными плоскостями на глубине z и z – dz. С учетом того, что длина образующей сферического кольца равна Rd β, площадь его поверхности определится формулой: S = 2 ⋅π⋅ r ⋅ R ⋅ d β. На поверхности сферического кольца действуют нормальные напряжения σ _R, а касательные напряжения в соответствии с гипотезой а) отсутствуют. Найдем напряжения σ _R из условия равновесия проекций всех сил, действующих по поверхности полусферы радиусом R, на вертикальную ось z. Условие равновесия:

         .                                                   (3.1)

В соответствии с гипотезой в) σ _R = A ⋅ cos β / R ². Кроме этого r = R ⋅ sin β. Подставляя в уравнение (3.1) выражения для σ _R и r и выполняя преобразования, получим:

Выполняем замену переменных в уравнении (3.2): u = cos β, du = − sin β⋅ d β. Продолжая преобразования, получим выражение для неопределенного коэффициента А:

Выразим cosβ через ординату z: cosβ = z / R. С учетом этого формула для определения напряжения σ _R будут иметь вид:

Практический интерес представляют напряжения на горизонтальной площадке, наклоненной к площадке, на которой действуют напряжения σ _R, под углом β. В соответствии с гипотезой б) главный вектор напряжений на горизонтальной площадке σ _R ′ совпадает по направлению с вектором напряжения σ _R, а его модуль равен σ _R ′ = σ _R ⋅cosβ. Проекции главного вектора напряжений σ _R ′ на координатные оси являются компонентами тензора напряжений на горизонтальной площадке. Поскольку главный вектор напряжений σ _R ′ совпадает по направлению с радиусом вектором R, направляющие косинусы вектора напряжений определяются формулами:

cos(σ _R ′, z) = z / R;     cos(σ _R ′, x) = x / R;     cos(σ _R ′, y) = y / R                      (3.4)

С учетом полученных выше зависимостей, компоненты тензора напряжений на горизонтальной площадке будут определятся формулами:

Формулу для σ _z обычно табулируют. Для этого выполняют следующие преобразования:

Коэффициент К, зависящий от безразмерного параметра r / z, приводится в справочных данных. Формулы (3.5) и (3.6) при z = 0, т.е. в точке приложения силы Р, дают бесконечные значения напряжений. Теоретически это объясняется тем, что сила Р действует на бесконечно малой площадке, в связи с чем напряжения на этой площадке стремятся к бесконечности. С практической точки зрения этот результат является некорректным и подлежит разрешению.

2. Напряжения в грунтовом массиве от действия группы сил. При нагружении линейно-деформируемой среды по аналогии с упругой средой применим принцип суперпозиций. Используя этот принцип, напряжение в грунтовом массиве от действия группы сил можно представить как сумму напряжений от действия отдельных сил. При этом слагаемые в указанной сумме могут определяться по формулам Буссинеска. Например, для загружения грунтового массива по схеме, представленной на рис. 3.2, нормальное напряжение на горизонтальной площадке на глубине z может быть определено по формуле:

 

 

...

...

 

Рис. 3.2. Напряжение в грунтовом массиве от действия группы сил.

 

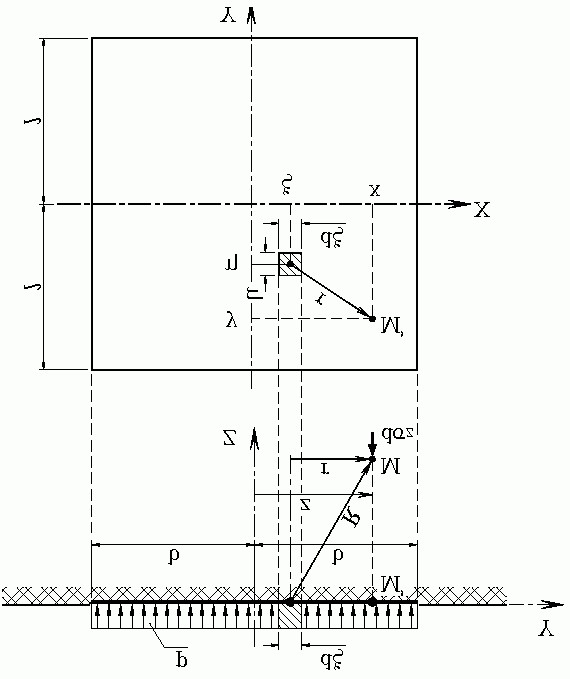
Анализ формулы (3.7) позволяет сделать следующий практически важный вывод: при неизменных давлениях на основание увеличение площади его нагружения приводит к увеличению напряжений в грунтовом массиве.

3. Напряжения от нагрузки, распределенной по прямоугольнику. Эта задача имеет большое прикладное значение, т.к. большинство фундаментов имеют прямоугольную форму подошвы  в плане. Кроме этого, при определении напряжений от распределенной нагрузки разрешается некорректность формул (3.5) и (3.6) при z = 0. Изобразим загруженную поверхность в плане (рис. 3.3). Совместим оси координат с центральными осями прямоугольника, ограничивающего загруженную давлением р (кПа) поверхность. Обозначим размеры прямоугольника: L, B – длина и ширина; l, b – полудлина и полуширина. Выделим на загруженной поверхности бесконечно малую площадку с координатами в центре площадки ξ и η и площадью d ξ⋅ d η. Элементарная сила, действующая на площадку, будет равна: dP = p ⋅ d ξ⋅ d η. Определим напряжение d σ _z в грунтовом массиве в точке с координатами x, y, z от элементарной силы dP, воспользовавшись формулой Буссинеска (3.5):

d

η

Рис. 3.3. Напряжение от нагрузки, распределенной по прямоугольнику:

Р – интенсивность нагрузки; l, b – полудлина и полуширина площади нагрузки.

 

В формуле (3.8) учтено, что радиус-вектор R соединяет точку с координатами x, y, z, в которой определяется напряжение, и точку с координатами ξ, η, 0, в которой действует элементарная сила. Для определения напряжения σ _z в точке с координатами x, y, z от всей загруженной площади проинтегрируем выражение (3.8) по загруженной площади:

Интеграл по формуле (3.9) имеет замкнутое аналитическое решение в тригонометрических функциях, впервые полученное в 1935 г. А. Лявом. Наиболее простые выражения для напряжений получаются по вертикалям в центральном сечении загруженной площади и по угловым точкам: σ _z = α⋅ p; σ _zc = α _c ⋅ p, где

Формулы (3.10) использованы в СНиП на проектирование оснований для вычисления напряжений под подошвой фундамента в центральном сечении и в угловой точке. Анализ выражений (3.10) позволяет сформулировать следующее определение: напряжения в угловой точке на глубине z равны ¼ напряжений в центральной точке на глубине z / 2. Это определение использовано в СНиП на проектирование оснований для вычисления коэффициента α _с по табулированному значению коэффициента α.

4. Метод угловых точек. Основывается по аналогии с формулой (3.7) на принципе суперпозиции. При этом для вычисления напряжений в любой точке грунтового массива используются формулы (3.10). Графические построения, связанные с техникой применения метода угловых точек для определения напряжений в грунтовом массиве, представлены на рис. 3.4. Различают два принципиально отличных случая применения метода угловых точек: вертикаль, по которой определяются напряжения, находится в пределах загруженной площади; вертикаль, по которой определяются напряжения, находится за пределами загруженной площади.

f

2

f

1

Рис. 3.4. Метод угловых точек: а – точка М расположена в пределах загруженной площади; б – точка расположена за пределами загруженной площади; в – точка М расположена за пределами загруженной площади в створе загруженной площади.

В первом случае (рис. 3.4 а) загруженная площадь разбивается на четыре прямоугольника, для которых точка, в которой определяется напряжение, является угловой. Напряжения определяются по формуле:

где α_c,i – коэффициенты по формуле (3.10) для прямоугольников 1 – 4.

Во втором случае (рис. 3.4 б) строится фиктивная площадь нагружения, границами которой являются две стороны прямоугольника с действительной нагрузкой, и точка, в которой определяется напряжение. Незагруженная площадь в фиктивном прямоугольнике разделяется на два пересекающихся прямоугольника, для которых, как и в первом случае, точка, в которой определяется напряжение, является угловой. Рассматриваются: прямоугольник, образующий фиктивную площадь нагружения (α _с,f); два пересекающихся прямоугольника (α _с,1 и α _с,2); прямоугольник области пересечения (α _с,cr). Напряжение вычисляется по формуле:

           σ z = p (α c, f −α c,1 −α c,2 +α c, cr).                                                        (3.12)

Здесь слагаемое, учитывающее влияние области пересечения, несмотря на отсутствие на ней нагрузки, входит в формулу со знаком «+», компенсируя тем самым двойное вычитание по этой области предыдущими членами формулы. Обобщая формулы (3.11) и (3.12), можно дать следующее определение методу угловых точек: напряжение в произвольной точке от нагрузки, распределенной по прямоугольной площади, равно алгебраической сумме напряжений в угловых точках прямоугольников, для которых рассматриваемая точка является угловой, при этом алгебраическая сумма площадей этих прямоугольников с учетом знаков в формуле суммирования напряжений должна совпадать с фактической площадью нагрузки. Используя это определение, непосредственно вытекающее из принципа суперпозиции, можно предложить самые различные схемы реализации метода угловых точек, например, для случая, представленного на рис. 3.4 в:

          σ z = p (α c, f 1 +α c f 2 −α c,1 −α c,2).                                                       (3.13)