
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над бинарными отношениями
Отношение, обратное к данному. Пусть F - бинарное отношение на множестве А. Тогда бинарное отношение на множестве А, состоящее из всех таких пар (а, b), что (b, а) Î Р, называется обратным (или инверсией) для F и обозначается через Таким образом, по определению
Например, если Fзадано равенством (*), то
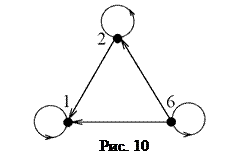
Как уже отмечалось, отношение F является областью истинности предиката пх делит у". Легко видеть, что Заметим, что если бинарное отношение F задано диаграммой, то диаграмма обратного к нему отношения Для иллюстрации обратимся снова к бинарному отношению F, заданному равенством (*). Его диаграмма построена на рис. 8. Диаграмма отношения
Очевидно, что любое бинарное отношение Fна множестве имеет обратное 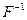 и и
Композиция. Пусть F и S - бинарные отношения, определенные на множестве А. Тогда их композицией называется бинарное отношение Таким образом, по определению
или
Пример. Пусть А = {а, b,с}, где а, b,с- различные элементы и F = {(а,а),(b,с)}, S = {(а, а), (а, b), (с, а), (с, b)}. Тогда F Примечание, Очевидно, что для отношений Fи S, указанных в предыдущем примере, равенство F Объединение, пересечение и разность бинарных отношений. Пусть F и S - какие-нибудь бинарные отношения на некотором множестве А. Тогда, по определению, каждое из отношений F и S является подмножеством множества А× А. Отсюда следует, что если применить к F и S одну из операций ("объединение ", "пересечение " либо "разность "), то снова получим подмножество множества А × А, т. е. - бинарное отношение на множестве А. Это означает, что можно говорить об операциях "объединения", "пересечения" и "разности" над бинарными отношениями на данном множестве А и использовать такие же символы для обозначения результатов этих операций как в теории множеств, т.е. Ç, È и \.
Таким образом, по определению, имеем: а) b) c) Пример. А, F и S- такие, как и в пункте 2. Тогда Свойства бинарных отношений Отношение F на множестве А называется рефлексивным, если (x, x) Î F для любого x Î A, т.е. если D Í F либо в другой записи: F - рефлексивно тогда и только тогда, когда Очевидно, что равенство является рефлексивным отношением. Отношение x > y не рефлексивно, однако отношение х ≥ у будет рефлексивным. Геометрически множество F, изображающее множество точек плоскости, принадлежащих данному отношению, содержит все точки прямой у = х. Отношение F на множестве А называется симметричным, если из того, что пара (x, у) Î F следует, что (у, x) Î F для любых х, у Î А:
или
Заметим, что если А = R, т. е. бинарное отношение задано множестве действительных чисел, то свойство симметричности имеет наглядное геометрическое выражение: множество пар действительных чисел, принадлежащих симметричному отношению, изображается множеством точек, симметричных относительно прямой у = х (рис. 11).
Отношение F называется транзитивным, если из того, что (x, у) Î F и (у, z) Î F следует, что пара (x, z) Î F для любых элементов х, у, z Î А, или
Например, отношение "больше" для действительных чисел транзитивно: если х > у и у > z, то и х > z. Отношение F называется антисимметричным, если из того, что (х,у) Î F и (у, x) Î F следует, что x = у, т.е.
Следующее предложение показывает, что каждое из определенных выше свойств бинарных отношений равносильно не которому свойству операций над этими отношениями. Предложение. Пусть F - произвольное бинарное отношение на некотором множестве А. Тогда: 1) F- рефлексивно Û D Í F, где D - диагональ на множестве А; 2) F- симметрично Û 3) F- транзитивно Û 4) F- антисимметрично Û Докажем, например, утверждение 2). Пусть F симметрично на множестве А и (х, у) Î Докажем обратное включение.
Пусть (x, y) Î F. Отсюда в силу симметричности отношения F следует, что (у, х) Î F, откуда, по определению, (х, у) Î Этим доказана импликация F - симметрично Þ Докажем обратную импликацию. Пусть
для любой пары (x, у) Î A× A и, значит, F - симметрично. Отношение порядка Рефлексивное, транзитивное и антисимметричное бинарное отношение называется отношением частичного порядка. Легко видеть, что известное отношение ≤ ("меньше либо равно") является отношением частичного порядка на любом множестве чисел. Другим классическим примером этого типа отношений является отношение Í "включения" на множестве Р(А) всех подмножеств произвольного фиксированного множества А. Бинарное отношение F на множестве А называется отношением строгого порядка, если оно антирефлексивно ((а, а) Ï F для любого а Î A), транзитивно и удовлетворяет дополнительному условию
Например, отношение "меньше" на множестве действительных чисел является отношением строгого порядка. В дальнейшем для обозначения отношения частичного порядка на произвольном множестве А, как правило, будет использоваться стандартный знак ≤. Фраза: "
Пусть Частично упорядоченное множество, в котором любые дваэлемента сравнимы, называется линейно упорядоченным или цепью. Пусть
Очевидно, что отношение ≥ также является отношением частичного порядка. Этот порядок называется двойственным к данному. Заметим, что если взять порядок, двойственный к ≥, то получим исходный порядок ≤. Ч.у. множество Пусть F - некоторое утверждение о ч.у. множествах, сформулированное в общелогических терминах (и терминах отношения частичного порядка). Утверждение В теории ч.у. множеств имеет место интересный факт, относящийся к теоремам этой теории. Принцип двойственности. Если некоторое утверждение Ф верно для всех упорядоченных множеств (т.е. является теоремой теории ч.у. множеств), то двойственное к нему утверждение также верно для всех ч.у. множеств. Подчеркнем еще раз значение слова "для всех" в формулировке принципа двойственности. Если какое-либо утверждение верно для конкретного ч.у. множества, то этот факт совсем не означает, что и двойственное утверждение будет верным вэтом частично упорядоченном множестве. Принцип двойственности позволяет "экономить на доказательствах" (избавляет от проведения лишней работы). Справедливость его имеет место в силу того, что утверждение Ф верно в ч.у. множестве
Таким образом, принцип двойственности является непосредственным следствием определений двойственного порядка и двойственного ч.у. множества. Однако для сомневающегося читателя мы можем предложить следующую схему рассуждений для обоснования этого принципа. Пусть Ф - утверждение, о котором говорится выше. Его можно представить в виде импликации Р Þ S двух предложений (Р - посылка, S - заключение утверждения Ф). Тогда утверждение
Пусть теперь утверждение Ф верно в любом частично упорядоченном множестве. Пусть Далее, очевидно, что Таким образом, из предположения справедливости Ниже будут приведены примеры применения принципа двойственности. Пусть
Двойственным образом получаем определение максимального элемента: Элемент а называется максимальным, если из х ≥ а следует х = а для любого х Î А. Это означает, что при построении предложения Элемент а называется наименьшим, если а ≤ х для всех х Î А. Двойственное понятие: Элемент а называется наибольшим, если а ≥ х для всех х Î А. Примеры: 1. Очевидно, что всякий наименьший элемент является минимальным. По принципу двойственности отсюда следует, что всякий наибольший элемент является максимальным. 2. Покажем, что если в ч.у. множестве Действительно, пусть a - наименьший элемент в А.
Предположим, что b также является наименьшим в А. Тогда, с одной стороны, а ≤ b, поскольку а - наименьший в А, а с другой - b ≤ а. Отсюда в силу свойства антисимметричности отношения ≤ следует, что а = b. Далее, пусть с - произвольный минимальный элемент в А. Тогда а ≤ с, поскольку а - наименьший, откуда в силу определения минимального элемента получим, что а = с. Отсюда по принципу двойственности справедливо следующее предложение: "Если ч.у. множество Предлагаем читателю в качестве интересного упражнение получить текст доказательства этого утверждения из доказательства предыдущего утверждения, заменив в нем каждую фразу двойственной. § 10. Отношение эквивалентности Наряду с отношениями порядка в математике особую роль играют бинарные отношения, которые одновременно обладают свойствами рефлексивности, симметричности и транзитивности. Любое такое отношение принято называть отношением эквивалентности или эквивалентностью на данном множестве. Для обозначения эквивалентности используется, как правило, стандартный знак ~. Например, запись x ~ y означает, что х находится в данном отношении ~ с у. Простейшим примером отношения эквивалентности на множестве X может служить отношение равенства между элементами этого множества. Укажем примеры отношений эквивалентности, которые не являются равенством. П р и м е р 1. Пусть т Î Z и m > 1. (Z - множество всех целых чисел). Определим бинарное отношение Fна множестве Z как область истинности предиката Р(х, у): " х - у делится на т". Это означает, что xFy Û либо в краткой записи xFy Û Покажем, что F - эквивалентность на множестве Z. 1. Рефлексивность отношения F. Поскольку
2. Симметричность отношения F.
3. Транзитивность отношения F. Пусть xFy и у Fz для некоторых чисел x, у, z Î Z. Тогда Отсюда получаем
Следовательно, П р и м е р 2. Пусть А, В- множества и f: A ® B - отображение. Определим на множестве А бинарное отношение S по правилу
для любых элементов Простая проверка показывает, что S - эквивалентность на множестве А. Это отношение называют ядром отображения f.
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.208 (0.054 с.) |
 .
.
 .
. , состоящее из всех пар (х,у) элементов множества А, для которых во множестве А существует элемент z такой, что (x, z) Î S и (z,у) Î S.
, состоящее из всех пар (х,у) элементов множества А, для которых во множестве А существует элемент z такой, что (x, z) Î S и (z,у) Î S.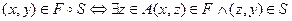

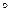 S = {(а, а), (а, b), (b, а), (b, b)}.
S = {(а, а), (а, b), (b, а), (b, b)}.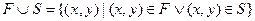 - объединение отношений F и S;
- объединение отношений F и S;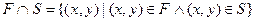 - пересечение отношений F и S;
- пересечение отношений F и S;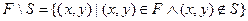 - разность отношений F и S.
- разность отношений F и S.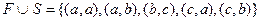 ,
, 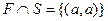 и
и 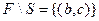 .
.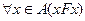 .
.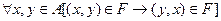 ,
,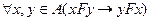 .
.
 .
.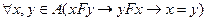 .
.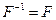 ;
;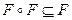 ;
;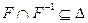 .
.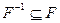 .
.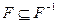 . Таким образом,
. Таким образом, 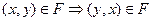
 .
.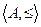 - частично упорядоченное множество" означает, что на множестве A задано отношение частичного порядка ≤.
- частично упорядоченное множество" означает, что на множестве A задано отношение частичного порядка ≤.
 Вместо слов "частично упорядоченное множество" используется также сокращенная запись "ч.у. множество".
Вместо слов "частично упорядоченное множество" используется также сокращенная запись "ч.у. множество".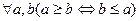 .
.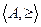 называется двойственным к ч.у. множеству
называется двойственным к ч.у. множеству  , полученное из Ф заменой всех вхождений знака ≤. на знак двойственного к нему отношения, называется утверждением, двойственным к Ф.
, полученное из Ф заменой всех вхождений знака ≤. на знак двойственного к нему отношения, называется утверждением, двойственным к Ф.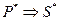
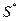 является следствием утверждения
является следствием утверждения 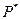 (об элементах множества А). Применим метод вспомогательной гипотезы. Предположим, что
(об элементах множества А). Применим метод вспомогательной гипотезы. Предположим, что  верно в двойственном ч.у. множестве
верно в двойственном ч.у. множестве 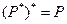 , т.е. Р верно в
, т.е. Р верно в 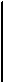



 Элемент а Î А называется минимальным, если из х ≤ а следует x = а для любого х Î А.
Элемент а Î А называется минимальным, если из х ≤ а следует x = а для любого х Î А.
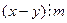
 , то
, то 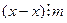 для любого числа x Î Z, откуда следует, что
для любого числа x Î Z, откуда следует, что




 Пусть xFy для некоторых чисел х, у Î Z. Тогда существует число k Î Z такое, что x – y = km, откуда y – x =(- k) m, т. е.
Пусть xFy для некоторых чисел х, у Î Z. Тогда существует число k Î Z такое, что x – y = km, откуда y – x =(- k) m, т. е. 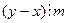 и, значит, yFx.
и, значит, yFx. и
и 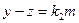 , где
, где 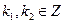 .
.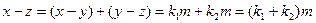 . 1
. 1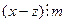 и, значит, xFz.
и, значит, xFz. 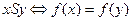
 .
.


